Поток вектора напряженности электрического поля в вакууме через любую замкнутую поверхность пропорционален алгебраической сумме зарядов, заключенных внутри этой поверхности

Применим полученную теорему для вычисления напряженностей от различных заряженных тел.

- Поле бесконечно заряженной плоскости. Из соображений симметрии, очевидно, что вектор напряженности поля Е должен быть направлен перпендикулярно к плоскости. Пусть плоскость пересечена цилиндрической поверхностью с образующими перпендикулярными к плоскости, и основаниями, параллельными ей (рис.10.2).

Поток напряженности через боковую поверхность равен нулю (силовые линии параллельны боковой поверхности). Поток через основания в силу теоремы Гаусса равен 2ES =, (10.6)Согласно (10.6) поле от такой плоскости однородно, перпендикулярно плоскости и не зависит от расстояния от плоскости.

- Поле плоского конденсатора. Если две пластины разноименно заряжены с поверхностной плотностью s, то поле в пространстве между пластинами конденсатора равно 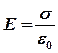(10.7) и сосредоточено между плоскостями. Это следует из рис.10.3, как и то, что вне пластин поле равно нулю.

- Поле заряженной сферы. Поле заряженной сферы обладает центральной симметрией, т.е. вектор E направлен по радиусам.

Согласно теореме Гаусса, поле внутри сферы Е=О, т.е. внутри сферы нет зарядов. Вне сферы, т.е. при r>R (R - радиус сферы), в силу теоремы 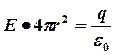или:

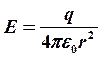(10.8)

Следовательно, поле заряженной сферы совпадает с полем точечного заряда, помещенного в центр сферы. В близи поверхности сферы поле равно

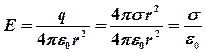
где σ – поверхностная плотность заряда сферы, а R = r.

Date: 2015-08-24; view: 402; Нарушение авторских прав