Законы Ома и Джоуля-Ленца. Дифференциальная форма закона Ома и Джоуля-Ленца

Как известно, закон Ома был установлен эмпирически и имеет вид

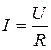(12.9)

В этой форме он справедлив для однородного участка проводника.

Закон Ома можно записать в дифференциальной форме. Выделим мысленно в окрестности некоторой точки внутри проводника элементарный цилиндрический объем с образующими, параллельными вектору плотности тока j в данной точке.

Через поперечное сечение цилиндра течет ток силой jdS. Напряжение, приложенное к цилиндру, Edl. Сопротивление цилиндра (рис.12.1) , где r - удельное сопротивление проводника. Подставив эти значения в формулу (12.9), получим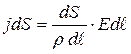

Носители заряда в каждой точке движутся в направлении вектора 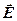. Поэтому 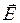и 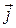по направлению совпадают и можно записать 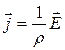, где 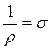-удельная проводимость проводника, то

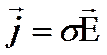Формула (12.10) выражает закон Ома в дифференциальной форме.

При прохождении по проводнику тока проводник нагревается. Джоуль и независимо от него Ленц экспериментально обнаружили, что

Q = I²Rt (12.11)

где Q - количество теплоты; I - сила тока; R - сопротивление проводника; t - время. От этой формулы (12.11), определяющей тепло, выделяемое во всем проводнике, можно перейти к выражению, характеризующему выделение тепла в отдельных малых участках проводника. Выделим элементарный объем в виде цилиндра, точно таким же образом, как и при выводе закона Ома. Согласно закону, за время dt в этом объеме выделится тепло:

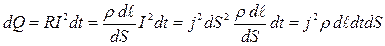
или учитывая, что dS d = dV, dQ= j² dV dt.

Количество тепла dQ, отнесенное к единице времени и единице объема, назовем удельной мощностью тока w. Кроме того, j = sE, а 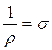, т.е. . Учитывая эти зависимости, можно записать: w = rj² = rs²E² =sE², т.е.

w = sE² (12.12)

Формула (12.12) выражает закон Джоуля-Ленца в дифференциальной форме.

Date: 2015-08-24; view: 783; Нарушение авторских прав