
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Лекция 14
|
|
Планирование траекторий манипулятора
Планирование траекторий движения манипулятора – это задача выбора закона управления, обеспечивающего движение манипулятора вдоль некоторой заданной траектории. Перед началом движения манипулятора важно знать:
1. существуют ли на его пути какие-либо препятствия;
2. накладываются ли какие-либо ограничения на траекторию схвата.
В зависимости от ответов на эти вопросы выбирается один из четырех типов управления манипулятором (табл. 14.1).
Таблица 14.1. Типы управления манипулятором
| Препятствия на пути манипулятора | |||
| Присутствуют | Отсутствуют | ||
| Ограничения на траекторию манипулятора | Присутствуют | I.Автономное планирование траектории, обеспечиваю-щее обход препятствий, плюс регулирование дви-жения вдоль выбранной траектории в процессе работы манипулятора | II.Автономное плани-рование траектории плюс регулирование движения вдоль выб-ранной траектории в процессе работы манипулятора |
| Отсутствуют | III.Позиционное управление плюс обнаружение и обход препятствий в процессе движения | IV.Позиционное управление |
Рассмотрим планирование траектории манипулятора при отсутствии препятствий (II и IV тип). Задача состоит в разработке математического аппарата для выбора и описания желаемого движения манипулятора между начальной и конечной точками траектории.
При планировании траекторий обычно применяется один из двух подходов:
1. Задается точный набор ограничений (например, непрерывность и гладкость) на положение, скорость и ускорение обобщенных координат манипулятора в некоторых (называемых узловыми) точках траектории. Планировщик траекторий после этого выбирает из некоторого класса функций (как правило, среди многочленов, степень которых не превышает некоторое заданное n) функцию, проходящую через узловые точки и удовлетворяющую в них заданным ограничениям. Определение ограничений и планирование траектории производится в присоединенных координатах.
2. Задается желаемая траектория манипулятора в виде некоторой аналитически описываемой функции, как, например, прямолинейную траекторию в декартовых координатах. Планировщик производит аппроксимацию заданной траектории в присоединенных или декартовых координатах.
Планирование в присоединенных переменных обладает тремя преимуществами:
1) задается поведение переменных, непосредственно управляемых в процессе движения манипулятора;
2) планирование траектории может осуществляться в реальном времени;
3) траектории в присоединенных переменных легче планировать.
4) Должны быть сведены к минимуму бесполезные движения типа «блуждания».
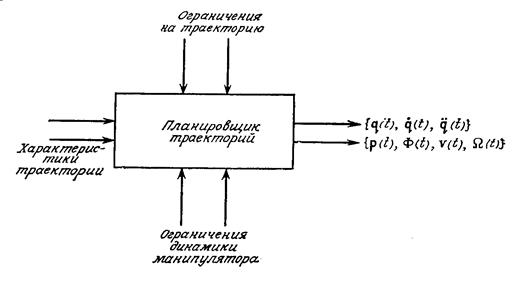
Рисунок 14.1. Блок-схема планировщика траекторий
Недостаток – сложность определения положения звеньев и схвата в процессе движения. Это необходимо для предотвращения столкновения с препятствием.
В общем случае основной алгоритм формирования узловых точек траектории в пространстве присоединенных переменных весьма прост:
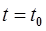 ;
;
цикл: ждать следующего момента коррекции;
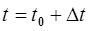 ;
;
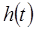 =заданное положение манипулятора в пространстве присоединенных переменных
=заданное положение манипулятора в пространстве присоединенных переменных
в момент времени 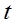 ;
;
Если 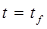 , выйти из процедуры;
, выйти из процедуры;
Выполнить цикл.
Здесь 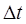 – интервал времени между двумя последовательными моментами коррекции параметров движения манипулятора.
– интервал времени между двумя последовательными моментами коррекции параметров движения манипулятора.
Из алгоритма видно, что все вычисления производятся для определения траекторной функции 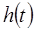 , которая должна обновляться в каждой точке коррекции параметров движения манипулятора.
, которая должна обновляться в каждой точке коррекции параметров движения манипулятора.
На планируемую траекторию накладывается четыре ограничения:
1) Узловые точки должны легко вычисляться нерекуррентным способом.
2) Промежуточные положения должны определяться однозначно.
3) Должна быть обеспечена непрерывность присоединенных координат и их двух первых производных, чтобы планируемая траектория в пространстве присоединенных переменных была гладкой.
4)
Перечисленным ограничениям удовлетворяют траектории, описываемые последовательностями полиномов.
В общем случае планирование траекторий в декартовых координатах состоит из двух последовательных шагов:
1) формирование последовательности узловых точек в декартовом пространстве, расположенных вдоль планируемой траектории схвата;
2) выбор некоторого класса функций, аппроксимирующих участки траектории между узловыми точками в соответствии с некоторым критерием (например, прямые, дуги круга, параболы и т.п.).
Первый подход позволяет обеспечить высокую точность движения вдоль заданной траектории. Однако, при отсутствии датчиков положения схвата в декартовых координатах, для перевода декартовых координат в присоединенные требуется большое количество вычислений, что замедляет время движения манипулятора. Поэтому используется второй подход – декартовы координаты узловых точек преобразуются в соответствующие присоединенные координаты с последующим проведением интерполяции в пространстве присоединенных переменных полиномами низкой степени. Это сокращает вычисления и позволяет учесть ограничения динамики манипулятора. Но точность движения снижается.
Date: 2015-08-15; view: 553; Нарушение авторских прав