Подвижные системы координат

Подвижные системы координат могут участвовать как во вращательном, так и в поступательном движениях относительно некоторой неподвижной инерциальной системы координат. На рис. 12.1 изображена подвижная система координат , которая совершает вращательное и поступательное движения относительно инерциальной системы координат 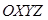. Положение материальной точки р, обладающей масcой m, относительно систем координат 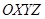и задается векторами r и r ^* соответственно. Положение точки О^* в системе координат 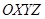определяется вектором h.

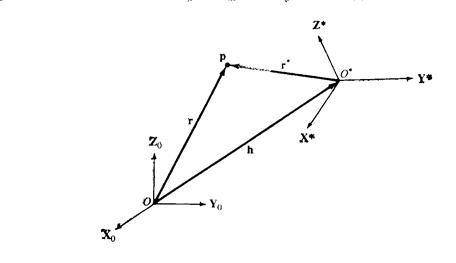
Рисунок 12.1. Подвижная система координат

Соотношения между векторами r и r^* даётся выражением (см. рис. 12.1):

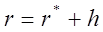. (12-1)

Если система координат движется относительно системы , то:

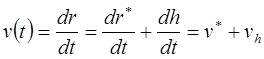, (12-2)

где 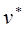и 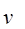- скорости точки р в системах координат и 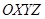соответственно, а 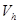- скорость точки 0^* в системе координат .

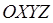С учетом равенства (11-13) выражение (12-2) представим:

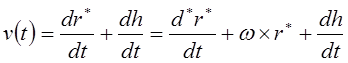. (12-3)

Аналогично ускорение точки р в системе координат :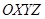

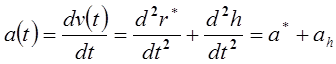, (12-4)

где 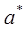и 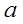- ускорения точки р в системах координат и 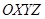соответственно, а 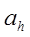- ускорение системы координат в инерциальной системе координат .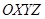

С учетом (11-14) равенство (12-4) можно представить в виде:

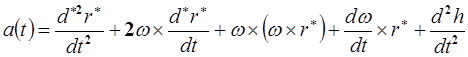. (12-5)

Полученные соотношения для подвижных систем координат применима к системам координат звеньев манипулятора.

Date: 2015-08-15; view: 1301; Нарушение авторских прав