Алгебраическая сумма внешних сил и сил инерции, действующих на тело в любом направлении, равна нулю»

Рассмотрим i- е звено (рис. 8.1). Пусть точка О' совпадает с центром масс этого звена. Устанавливая соответствие между рис. 11.4 и 13.1, введем следующие обозначения (все векторы заданы в базовой системе координат):

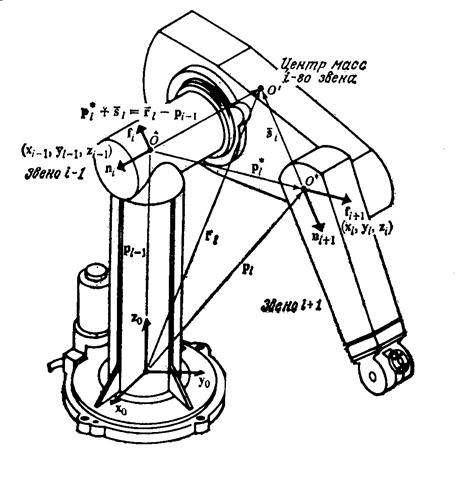
Рисунок 13.1. Силы и моменты, действующие на i-е звено

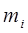- масса i- го звена;

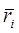- положение центра масс i- го звена в базовой системе координат;

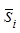- положение центра масс i- го звена относительно начала

системы координат ;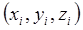

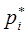- положение начала i- й системы координат относительно

начала -й системы координат;

- линейная скорость центра масс i- го звена;

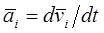- линейное ускорение центра масс i- го звена;

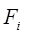-суммарная внешняя сила, приложенная к центру масс

i- го звена;

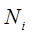-суммарный момент внешних сил, приложенных к i- му

звену;

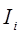- матрица инерции i- го звена относительно его центра

масс в базовой системе координат ;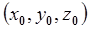

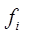- сила, с которой -е звено действует на i- е звено в

системе координат ;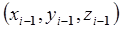

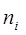- момент, вызванный действием -го звена на i- е

звено в системе координат .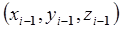

Пренебрегая силами трения в сочленениях, применив принцип Д'Аламбера к i- му звену, получаем:

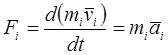, (13-1)

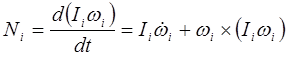. (13-2)

Входящие в эти формулы линейные скорость и ускорение центра масс i- го звена в соответствии с равенствами (12-32) и (12-35) определяются выражениями:

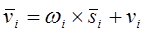, (13-3)

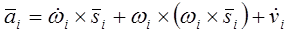. (13-4)

Суммарная сила 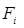и момент 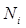, приложенные к i- му звену, обусловлены действием на него силы тяжести, а также сил со стороны соседних -го и 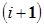-го звеньев. Таким образом:

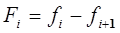, (13-5)

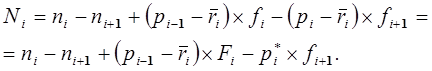(13-6)

Эти уравнения можно представить в рекуррентной форме, воспользовавшись тем, что:

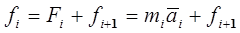, (13-7)

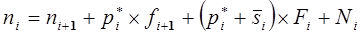. (13-8)

Полученными уравнениями, имеющими рекуррентную форму, можно воспользоваться для вычисления сил и моментов 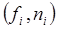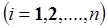, действующих на звенья n -звенного манипулятора. Для этого достаточно учесть, что 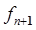и 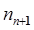представляют собой соответственно силу и момент, с которыми объект манипулирования действует на схват манипулятора. Момент, создаваемый приводом i- го сочленения, должен быть равен сумме проекции момента 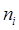на ось 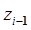и момента вязкого трения в i- м сочленении (если сочленение – вращательное). Если же i- е сочленение – поступательное, оно реализует смещение на 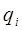единиц длины относительно системы координат 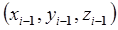вдоль оси 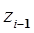. В этом случае сила 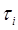, создаваемая в этом сочленении, должна быть равна в системе координат 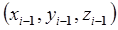сумме проекции силы 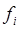на ось 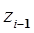и силы вязкого трения. Таким образом, момент (сила) 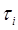, создаваемый приводом i- го сочленения, определяется формулой:

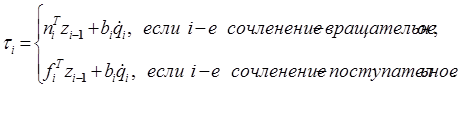, (13-9)

где 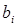- коэффициент вязкого трения в i -м сочленении.

Если основание манипулятора закреплено на платформе и 0-е звено неподвижно, то , , 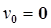и с учетом силы тяжести:

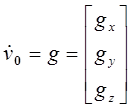, где 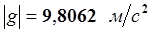. (13-10)

Таким образом, для исследователя существует возможность выбора одной из трех следующих форм представления уравнений движения манипулятора:

1. удобная для анализа, но неэффективная в вычислительном плане форма Лагранжа-Эйлера;

2. эффективная с вычислительной точки зрения, но малопригодной для анализа форма Ньютона-Эйлера;

3. достаточно удобные для анализа при умеренных вычислительных затратах обобщенные уравнения Д'Аламбера.

Date: 2015-08-15; view: 541; Нарушение авторских прав