Построение алгоритма вычислений

1. Исходные данные

m _[1] , m_2, m₃, m₄, С₁, С₂, м, , R₂, R₄, p, F₀, g, y₀, .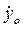

2. Вычисление констант

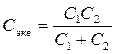
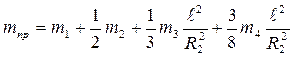
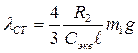
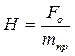
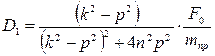
3. Задание начального времени t=0.

4. Вычисление значений функций в момент времени t.

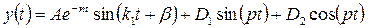
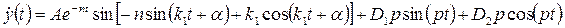
5. Вычисление реакций связей.

Т₁₂ = F₀ sin (pt) + m₁g – m₁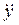

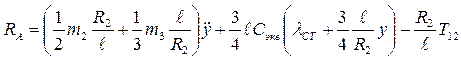
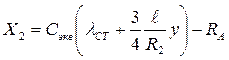
Y₂ = m₁g + m₃g + T₁₂

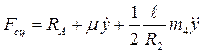
6. Вывод на печать значений искомых функций в момент времени t.

7. Определение значения времени на следующем шаге t₁ = t +Δ t

8. Проверка условия окончания цикла t ≤ t_кон

9. Возврат к пункту 4.

Проведем подготовку данных к вычислениям, используя заданные исходные числовые данные для рассматриваемого примера. Произведя вычисление констант, получаем:

; m_пр = 12 кг; λ_СТ = 0,32 м; k = 3,02 с^-1; k₁ = 2,58 с^-1;

n= 1,56 c^-1; 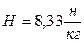; D₁ = -0,28; D₂ = - 0,51; A=1,44; β=0,51 рад.

Замечаем, что 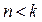, т.е. имеем случай малого сопротивления.

Тогда для данного числового примера выражения для закона движения, скорости и ускорения ведущего тела имеют вид

у (t) = 1,44 e^-1,56t sin (2,58 t + 0,51) – 0,28 sin 4 t – 0,51 cos 4 t (м)

= 1,44 e^-1,56t [-1,56 sin (2,58 t +0,51) +2,58 cos (2,58t +0,51)] –

-2,04 sin 4t – 1,12 cos 4t (м/с)

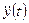= - 3,12 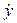– 9,12 у + 8,33 sin 4 t (м/с²)

2.9.Работа на компьютере

Вычисления производятся по составленной программе в дисплейном классе кафедры. Работа с программой осуществляется в диалоговом режиме. Результаты вычислений выводятся на экран дисплея для оперативного анализа в виде графиков (приложение 1).

Полученная математическая модель движения системы адекватно описывает малые колебания системы только в случае, когда нить (или нити – в некоторых схемах механизмов) находятся в состоянии натяжения. Это значит, что силы натяжения нитей должны быть положительными на всем интервале движения системы.

При введении заданных числовых значений и последующем вычислении искомых функций может получиться, что в некоторые промежутки времени, значения сил натяжения нитей могут оказаться отрицательными. Это означает, что надо изменить задаваемые параметры системы так, чтобы силы натяжения нитей стали положительными на всем интервале движения системы, т.е. нити должны все время быть в состоянии натяжения.

Предлагается изменить массу 1 тела так, чтобы обеспечить положительные значения сил натяжения нитей на всем интервале движения системы.

СПИСОК ЛИТЕРАТУРЫ

1. А.А.Яблонский, С.С. Норейко. Курс теории колебаний. М.: Высшая школа, 1975г и последующие издания

2.Я.Г. Пановко Введение в теорию механических колебаний.М.: Наука, 1971г и последующие издания.

3. Л.М. Нечаев Введение в теорию колебаний механических систем. Учебное пособие.-Тула.: ТГТУ, 1996,104с.