Вынужденные колебания системы с одной степенью свободы

Вынужденные колебания совершает механическая система, на которую наряду с упругими силами действуют периодически изменяющиеся силы, называемые возмущающими силами.

Пусть на одно из тел системы действует возмущающая сила, изменяющаяся по гармоническому закону

(1.27)

где F_o - амплитуда силы, р - частота, δ - начальная фаза.

Дифференциальное уравнение вынужденных колебаний системы с одной степенью свободы с учетом сил сопротивления имеет вид [1,2,3]:

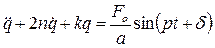, (1.28)

где .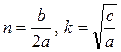

Из этого уравнения легко получить дифференциальное уравнение вынужденных колебаний системы с одной степенью свободы без учета сопротивления, положив в (1.28) n=0, получаем:

(1.29)

Общее решение неоднородного дифференциального уравнения (1.28)

Можно найти как сумму двух решений: решения однородного дифференциального уравнения (1.11) и частного решения данного неоднородного дифференциального уравнения (1.28).

Решение однородного дифференциального уравнения (1.11) подробно рассмотрено в предыдущем параграфе.

Вид частного решения определяется видом правой части дифференциального уравнения (1.28).

Рассмотрим случай, когда закон изменения возмущающей силы имеет вид:

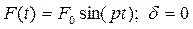(1.30)

Для нашего случая частное решение ищем в виде:

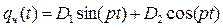(1.31)

Подставляя (1.31) в (1.28) с учетом (1.30), после несложных преобразований, получаем:

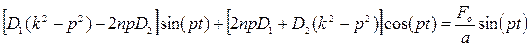(1.32)

Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения постоянных D₁ и D₂:

(1.33)

Решая эту систему, получаем следующие выражения для коэффициентов D₁ и D₂:

(1.34)

Таким образом, частное решение (1.31) определено.

Складывая теперь частное решение с решением однородного дифференциального уравнения (1.11), получаем уравнение движения системы, совершающей вынужденные колебания в среде с сопротивлением:

(1.35)

Вид решения однородного уравнения зависит от степени действующего на систему сопротивления среды.

Так, для случая малого сопротивления (n < k) имеем:

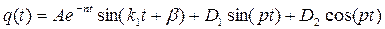(1.36)

Постоянные А и β определяются из начальных условий q(0)=q₀ и .

Для этого найдем еще производную по времени от q(t) (1.36):

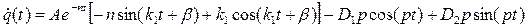(1.37)

Подставляя начальные условия в (1.36) и (1.37) получаем систему алгебраических уравнений:

Решая эту систему, получаем:

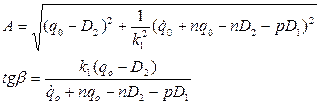(1.38)

Таким образом, константы D₁, D₂, A, β в уравнении (1.36) определены, и следовательно получен закон вынужденных колебаний механической системы с одной степенью свободы для случая малого сопротивления (n < k).

Очевидно, что для случая большого сопротивления (n> k) общее решение уравнения (1.28) будет

(1.39)

А для случая достаточно большого сопротивления (n=k),будем иметь:

(1.40)

Константы А₁ и γ в уравнении (1.39) и С₁ и С₂ в уравнении (1.40) определяются по начальным условиям движения q₀ и 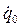. Процедура определения констант описана выше для случая малого сопротивления.

2.КУРСОВАЯ РАБОТА «ИССЛЕДОВАНИЕ ДВИЖЕНИЯ МЕХАНИЧЕСКОЙ СИСТЕМЫ С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ ПРИ НАЛИЧИИ УПРУГИХ СВЯЗЕЙ»

Целью курсовой работы является приобретение навыков получения математической модели описывающей движение механической системы с одной степенью свободы с упругими связями путем составления дифференциального уравнения движения с помощью основных теорем и принципов теоретической механики и его дальнейшего решения аналитическим методом, а также проведение последующего численного анализа динамического поведения механической системы.

Date: 2015-08-15; view: 2144; Нарушение авторских прав