
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Затухающие колебания системы с одной степенью свободы. В реальных условиях свободные колебания механической системы происходят при наличии сил сопротивления
|
|
В реальных условиях свободные колебания механической системы происходят при наличии сил сопротивления, вызывающих рассеивание
(диссипацию) механической энергии системы.
Предположим, что силы сопротивления, действующие на тела системы пропорциональны скорости
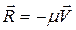 (1.10)
(1.10)
где μ- коэффициент сопротивления среды.
В этом случае дифференциальное уравнение затухающих колебаний системы имеет вид [1,2,3]
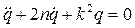 (1.11)
(1.11)
где 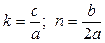 (1.12)
(1.12)
b -называется обобщенным коэффициентом сопротивления или коэф-фициентом диссипации. Коэффициент n называется коэффициентом затухания и характеризует сопротивление среды.
Интегрирование этого уравнения производим по общему правилу интегрирования однородных линейных дифференциальных уравнений с постоянными коэффициентами.
Составим характеристическое уравнение и найдем его корни:
 (1.13)
(1.13)
В зависимости от соотношения величин n и k возможны три различных случая:
1.В случае малого сопротивления, когда n<k, корни характеристического уравнения комплексно-сопряженные, поэтому движение системы представляет собой затухающие колебания.
2.В случае большого сопротивления, когда n>k, корни характеристического уравнения действительные и разные, поэтому движение системы будет апериодическим.
3.В случае достаточно большого сопротивления при n=k корни характеристического уравнения действительные и кратные, поэтому будет иметь место предельное апериодическое движение системы.
Затухающие колебания. При n < k общее решение уравнения (1.11) имеет вид:
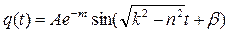 (1.14)
(1.14)
Здесь постоянные А и β определяются по начальным условиям и имеют вид:
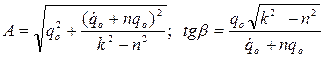 (1.15)
(1.15)
Движение системы в рассматриваемом случае (n<k) носит колебательный характер.
График этих колебаний изображен на рисунке 2.
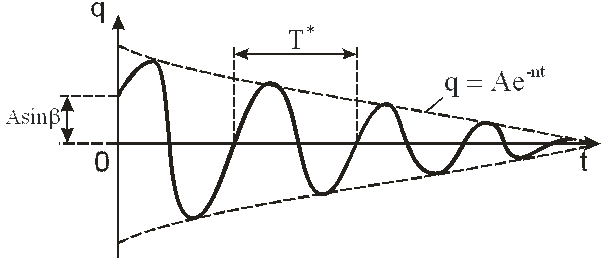
Рисунок 2.
Множитель е-nt указывает на то, что амплитуда затухающих колебаний с течением времени уменьшается. Циклической частотой затухающих колебаний называется величина 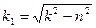 . (1.16)
. (1.16)
Тогда период затухающих колебаний
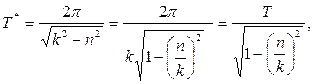 (1.17)
(1.17)
где 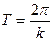 - период свободных колебаний системы при отсутствии сопротивления (n=0).
- период свободных колебаний системы при отсутствии сопротивления (n=0).
Так как промежуток времени, отделяющий моменты двух наибольших последовательных отклонений системы от ее положения равновесия, соответствует полупериоду колебаний Т*/2, то значения этих отклонений будут следующими:
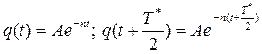 (1.18)
(1.18)
Отношение двух последовательных амплитуд называется декрементом колебаний η, эта величина остается постоянной во все время колебательного движения:
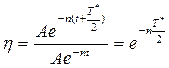 (1.19)
(1.19)
Логарифмическим декрементом колебаний называется величина:
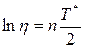 (1.20)
(1.20)
Апериодическое движение. В случае большого сопротивления при n > k движение системы теряет колебательный характер и является апериодическим. Общее решение дифференциального уравнения (1.11) ищем в виде:
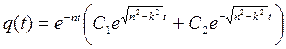 (1.21)
(1.21)
Используя необходимые преобразования, общее решение можно записать в виде:
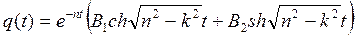 (1.22)
(1.22)
Новые постоянные интегрирования В1 и В2 можно заменить другими постоянными А1 и γ по условию:
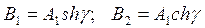 (1.23)
(1.23)
Тогда, уравнение движения системы примет вид
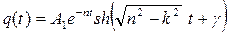 (1.24)
(1.24)
Уравнение движения системы (1.24) показывает, что движение системы не является колебательным, так как гиперболический синус не является периодической функцией.
График этого апериодического движения системы представлен на рисунке 3.
Предельное апериодическое движение. При достаточно большом сопротивлении n=k общее решение дифференциального уравнения (1.11) имеет вид:
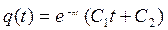 (1.25)
(1.25)
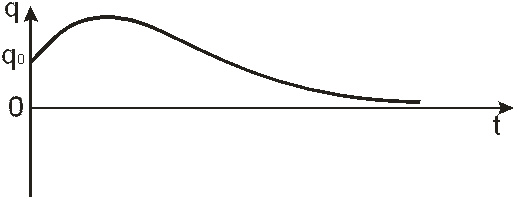
Рисунок 3
Определив С1 и С2 по начальным условиям движения, уравнение (1.25) принимает вид:
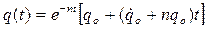 (1.26)
(1.26)
В этом случае движение системы является также апериодическим.
Рассмотрев влияние сопротивления, пропорционального скорости, на движение системы с одной степенью свободы, можно сделать следующие выводы:
1.Силы сопротивления, совершая отрицательную работу, вызывают непрерывное уменьшение амплитуды затухающих колебаний системы.
2.Влияние малого сопротивления на частоту и период колебаний системы незначительно, однако даже очень малое сопротивление вызывает затухание этих колебаний.
3.При большом сопротивлении происходит апериодическое движение системы, т.е. колебательный процесс отсутствует.
Date: 2015-08-15; view: 669; Нарушение авторских прав