Свободные колебания системы с одной степенью свободы. Механическая система с голономными, стационарными и идеальными связями может совершать свободные колебания около положения устойчивого равновесия при наличии

Механическая система с голономными, стационарными и идеальными связями может совершать свободные колебания около положения устойчивого равновесия при наличии упругих связей, которые являются источником появления упругих сил, действующих на систему.

Дифференциальное уравнение свободных колебаний системы имеет вид [1,2,3]:

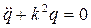(1.1)

где - называется циклической частотой свободных колебаний,

с- приведенная жесткость системы, а –приведенная масса системы или коэффициент инерции.

Из характеристического уравнения 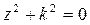находим корни этого уравнения: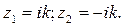

Общее решение дифференциального уравнения (1.1) ищем в виде:

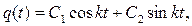(1.2)

откуда

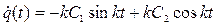. (1.3)

Постоянные интегрирования С₁ и С₂ определяем из начальных условий, которые подставляем в (1.2) и (1.3):

С учетом найденных констант интегрирования, уравнение движения системы имеет вид

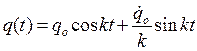(1.6)

Общее решение (1.2) дифференциального уравнения (1.1) можно представить и в другом виде, положив С₁=А sin α и C₂=A cosα, где А и α – две новые произвольные постоянные.

Подставляя С₁ и С₂ в (1.2), получаем

или

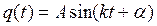(1.7)

Тогда

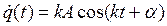
и с учетом начальных условий, получаем:

Откуда

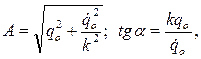(1.8)

где А – амплитуда свободных колебаний, α – начальная фаза колебаний.

Период свободных колебаний системы

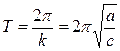(1.9)

Из формул, определяющих частоту и период свободных колебаний, следует, что частота и период не зависит от начальных условий, а зависят лишь от внутренних параметров системы. Так период свободных колебаний увеличивается при увеличении приведенной массы системы а и уменьшается при увеличении приведенной жесткости системы с.

График свободных колебаний изображен на рисунке 1.

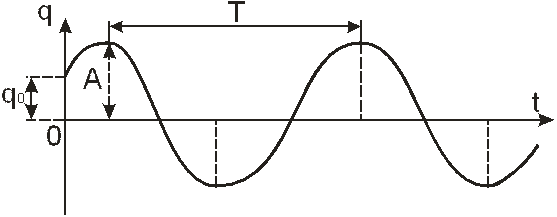
Рисунок 1.

Date: 2015-08-15; view: 554; Нарушение авторских прав