Механическая часть электропривода как объект управления

Анализ динамических свойств механической части электропривода проводят решением уравнения движения электропривода как объекта управления по принятым расчетным схемам, исследуя переходные режимы.

Переходным процессом электропривода как динамической системы является режим его работы при переходе от одного установившегося состояния к другому, когда изменяется ток, момент и скорость двигателя.

Детальный анализ свойств упругих механических систем обычно проводят на основе двухмассовой расчетной схемы. Для устранения перекрестной связи в структурной схеме, приведенной на рис.3.7,. выполним ее преобразование переносом внутренней связи по упругому моменту на выход системы.

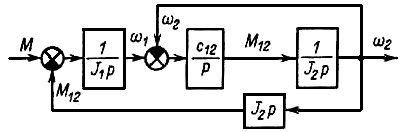
Рис.3.8 Преобразованная структурная схема

Определим передаточные функции системы, связывающие между собой скорости ω₂ и ω₁, скоростей ω₂ и ω₁, с электромагнитным моментом двигателя М М по полученной структурной схеме (рис.3.8).

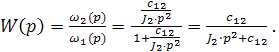
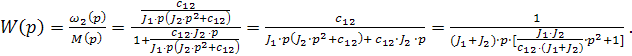
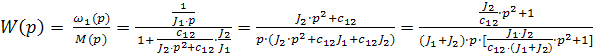(3.19)

Характеристическое уравнение системы с выходом по моменту получим из передаточных функций (3.19): 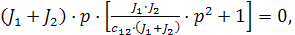(3.20)

корни которого:. 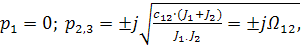(3.21)

где W₁₂ - резонансная частота двухмассовой упругой системы.

Наличие мнимых корней свидетельствует о том, что система находится на грани устойчивости и если ее вывести из состояния равновесия, то переходный процесс будет незатухающим с частотой W₁₂.

Обозначим 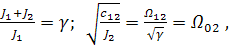(3.22)

где γ – коэффициент соотношения масс;

W₀₂ – резонансная частота 2-й инерционной массы при J₁ ®¥ (при жесткой заделке первой).

С учетом принятых обозначений передаточные функции системы (3.19) будут иметь вид:

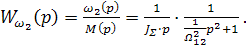(3.23)

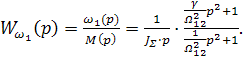(3.24)

Скорость ω₂ в двухмассовой механической системе является скоростью вращения рабочего механизма, а ω₁ - скоростью вращения электродвигателя.

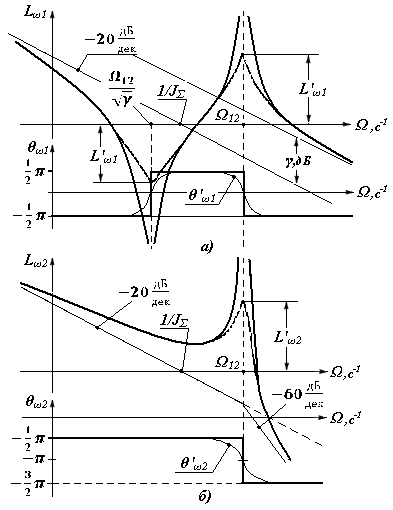
Рис.3.9 Логарифмические частотные характеристики упругой двухмассовой системы по управляющему моменту по

а) - скорости 1-й массы, б) – скорости 2-й массы

Асимптотические логарифмические (ЛАЧХ) на рис.3.9 построены непосредственно по полученным передаточным функциям системы. В соответствии с (3.24) структурная схема системы по ω₁ представлена последовательным соединением интегрирующего звена, форсирующего звена второго порядка с частотой сопряжения W_c1=W₁₂/ 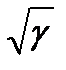и консервативного звена с резонансной частотой W_c2=W₁₂. При W=W_С1 имеет место нуль передаточной функции консервативного звена и ЛАЧХ при этом терпит разрыв, стремясь к -¥. При W = W₁₂ имеет место полюс передаточной функции, при котором амплитуды стремятся к +¥, образуя второй разрыв. Низкочастотная асимптота определяется интегрирующим звеном с коэффициентом 1/J_Σ и соответственно имеет наклон -20 дБ/дек. Высокочастотная асимптота (W>>W₁₂) соответствует также интегрирующему звену, но при коэффициенте в g раз большем, чем в области низких частот (рис.3.9а).

В низкочастотной области сдвиг между колебаниями определяется интегрирующим звеном и составляет -90°. При W=W₁₂/ 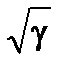скачком меняет знак числитель (3.24), что соответствует уменьшению фазового сдвига на 180°. Затем на частоте W=W₁₂ аналогично изменяется знак знаменателя, и фазовый сдвиг вновь принимает значение -90° в соответствии с высокочастотной асимптотой ЛАЧХ.

Структурная схема системы при выходной переменной ω₂ представлена интегрирующим и консервативным звеньями с передаточным коэффициентом 1/J_Σ и резонансной частотой W_c2=W₁₂, ЛЧХ которой представлены на рис. 3.9б. Они построены по передаточной функции (3.23), отличающейся от (3.24) только равенством числителя единице. В низкочастотной области ЛАЧХ L_w2 совпадает с L_w1, разрыв имеет место только на резонансной частоте W₁₂ и в высокочастотной области стремится к асимптоте с наклоном -60 дБ/дек. Соответственно фазовый сдвиг между колебаниями при этом составляет -270°.

Рассмотрим влиянии упругости на движение первой и второй масс механической части системы по ее структуре, представленной на рис.3.7, и частотными характеристиками, изображенными на рис.3.9. Движение первой массы при небольших частотах колебаний управляющего воздействия М в соответствии с (3.24) и рис.3.9а определяется суммарным моментом инерции электропривода J_Σ, при этом механическая часть ведет себя как интегрирующее звено. В частности, при М = const скорость ω₁ изменяется по линейному закону, на который накладываются колебания, обусловленные упругой связью. Таким образом, интегрирующее звено в структуре характеризует условия движения механической части в среднем.

При частотах колебаний управляющего сигнала (момента), близких к резонансной W₁₂, амплитуды колебаний скорости w₁ возрастают и при W₁=W₁₂ стремятся к бесконечности. Проявление резонанса зависят от параметров механической части, т.к. в числитель передаточной функции W_w1 входит уравнение форсирующего звена второго порядка. Влияние упругости на движение первой массы будет меньше, если рабочий механизм обладает небольшой инерцией (J₂<<J₁, g®1), так же, как если W₁₂®¥ в области малых и средних частот, то движение первой массы будет близко к движению, определяемому интегрирующим звеном W_и=J_S/p.

В низкочастотной области асимптоты ЛАЧХ L_w1 и L_w2 совпадают, и в среднем движение второй массы также определяется интегрирующим звеном W_и=J_S/p. Однако при W>W₁₂ наклон высокочастотной асимптоты L_w2 составляет -60 дБ/дек, и колебательность второй массы будет выше, чем первой, при этом независимо от значений g нет факторов, которые ослабляли бы развитие резонансных колебаний.

Определим уравнения движения первой и второй масс, момента упругой деформации.

Дифференциальное уравнение системы по скорости первой массы имеет вид:

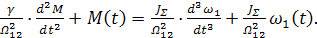(3.25)

С учетом того, что M=const, уравнение примет вид:

(3.26)

где ε_ср=M/J_Σ – среднее ускорение системы.

Корни характеристического уравнения определены выше: p₁=0, p_2,3=±jΩ₁₂.

Учитывая частное решение при нулевом корне. соответствующее установившемуся равномерно ускоренному движению системы 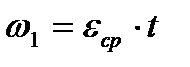и то, что два корня мнимые, общее решение приведенного выше дифференциального уравнения имеет вид:

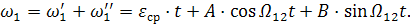(3.27)

С учетом начальных условий при t=0 w₁=0 и 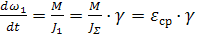получим A=0 и 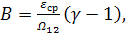тогда решение уравнения будет:

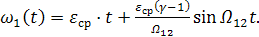(3.28)

Аналогично определяется на основании передаточной функции (3.23) изменение скорости второй массы системы:

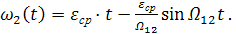(3.29)

Решая (3.18) из системы уравнений движения электропривода с учетом (3.29) получим закон изменения упругого момента системы:

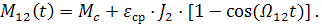(3.30)

Полученные соотношения показывают, что угловые скорости первой и второй масс, изменяются по периодическому закону около среднего значения скорости ω_ср = ε_ср · t, находясь в противофазе, с амплитудами, зависящими от масс и коэффициента упругой связи между ними.

Момент упругой деформации также имеет периодический характер, изменяясь от статического момента сопротивления. Графики изменения упругого момента и угловой скорости первой массы приведены на рис.3.10.

При прочих равных условиях колебания скорости ω₁ тем меньше, чем меньше J ₂, а увеличение Ω₁₂ при тех же ускорениях ε _ср снижает амплитуды колебаний скорости обеих масс.

Если J₂ << J₁ или Ω₁₂ → ∞ и не требуется оценка качества движения второй массы, возможен переход от двухмассовой к одномассовой механической системе. Тогда механическая часть, представленная в виде жёсткого приведённого звена, отражает движение системы в среднем и не даёт точных представлений о характере движения упруго связанных масс электропривода.

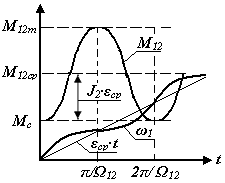
Рис.3.10 Графики изменения упругого момента

и скорости первой массы

Рассмотрим влияние упругих связей на динамику двухмассовой системы.

Максимальное значение упругих колебаний в двухмассовой системе из (3.30):

.

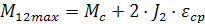Отклонение амплитуды колебаний от среднего значения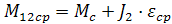

характеризуется динамическим коэффициентом 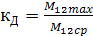, который является важной характеристикой условий работы механического оборудования и одним из основных показателей динамических качеств ЭП.

Упругие колебания в механической части электропривода неблагоприятно сказываются на его работе, т.к. увеличивают динамические нагрузки, вызывают неравномерность движения, которая снижает точность выполнения технологического процесса.

Динамический коэффициент может быть понижен ограничением темпа нарастания момента двигателя (рывка) при пуске.

Если 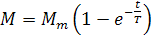и пусть М_С=0, тогда .

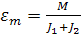Средние значения скорости первой массы и упругого момента будут иметь экспоненциальный характер, изменения которых приведены на рис.3.11.

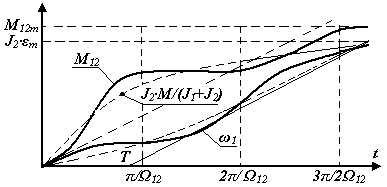
Рис.3.11 Демпфирование упругих колебаний ограничением «рывка»

В реальных системах присутствуют силы внешнего и внутреннего вязкого трения, оказывающие на систему демпфирующее воздействие. Для двухмассовой системы моменты сопротивления от сил внешнего вязкого трения на первой J₁ и второй J₂ массах пропорциональны скоростям соответствующих масс:

M_f1=a₁·ω₁, M_f2=a₂·ω₂,

где a₁, a₂ − коэффициенты пропорциональности.

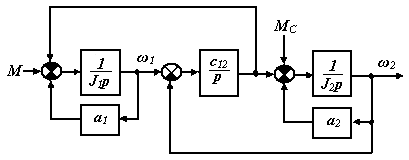
Рис.3.12 Структурная схема двухмассовой системы

с учетом сил внешнего вязкого трения

На структурной схеме (рис.3.12) с учетом этих сил сопротивления интегрирующие звенья масс охватываются жесткими отрицательными обратными связями, что приводит к потере интегрирующих свойств двухмассовой модели и появлению статической ошибки в системе. Установлено, что в технических системах влияние внешнего вязкого трения на динамические свойства системы незначительно и им можно пренебрегают.

На колебательную систему действуют кроме внешних демпфирующие внутренние силы вязкого трения. Влияние сил внутреннего вязкого трения в материале упругой связи выражают моментом сопротивления, пропорциональном разности скоростей ω₁ и ω₂:

M_вт = β_вт · (ω₁ – ω₂),

где β_вт – коэффициент пропорциональности.

Определим передаточную функцию замкнутой системы по скорости второй массы с учетом влияния внутреннего вязкого трения по структурной схеме, приведенной на рис.3.13.

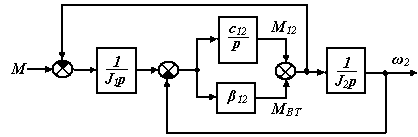
Рис.3.13 Структурная схема двухмассовой системы

с учетом влияния внутреннего вязкого трения

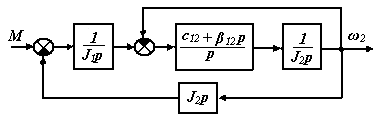
Рис.3.14 Преобразованная структурная схема системы

с учетом внутреннего вязкого трения

Преобразуя структурную схему, как показано на рис.3.14, получим:

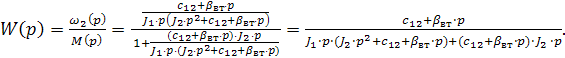(3.31)

Характеристическое уравнение системы из (3.31) будет:

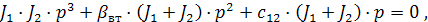
корни которого p₁=0, ,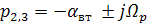

где 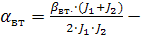коэффициент затухания,

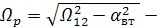резонансная частота.

Наличие комплексных сопряженных корней характеристического уравнения является показателем отсутствия незатухающих колебаний за счет демпфирования колебаний в механической системе силами внутреннего вязкого трения. Учет естественного демпфирования ограничивает резонансный пик ЛАЧХ конечными значениями и несколько сглаживает ЛФЧХ, показанные на рис.3.9а и 3.9б, как L'_ω1 θ'_ω1 L'_ω2 θ'_ω2 .

В реальных системах всегда имеются силы типа внутреннего вязкого трения, поэтому колебания скоростей со временем затухают. Однако, естественное затухание невелико и за время затухания совершается от 10 до 30 колебаний. C учетом вязкого трения, т.е. естественного демпфирования, скорости w₁ и w₂ и упругий момент в отличие от (3.28 - 3.30) изменяются по законам:

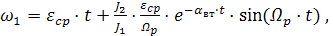
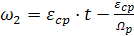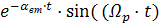· . (3.32)

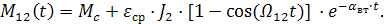
Динамические колебательные процессы в среднем не влияют на длительность переходных процессов, однако они во многих случаях отрицательно сказываются на точности работы установки, увеличивают динамические нагрузки и ускоряют его износ.