Напряжения на произвольной косой площадке

Зная напряжения на 3 ортогональных площадках, проходящих через одну точку, можно определить напряжения, действующие на любой другой плоскости, проходящей через эту точку.

Произвольная площадка характеризуется вектором нормали V,который раскладывается на компоненты по осям x,y,z. 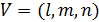. Эти компоненты являются косинусами углов между нормалью и осями координат.

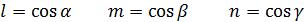- направляющие косинусы.

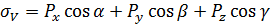- нормальное напряжение, действующее на произвольной площадке, равно сумме составляющих действующей силы по трем осям. (1)

Выразим через напряжения на трех ортогональных плоскостях через условия равновесия:

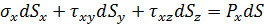
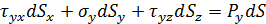
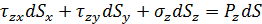
Подставим вместо

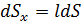
Сократим на dS и получим:

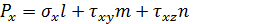
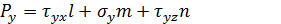
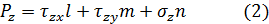
Подставим уравнение (2) в уравнение (1) получим:

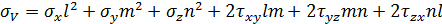
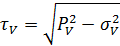
5. Главные площадки и главные напряжения. Инварианты напряженного состояния в точке. Тензор напряжений.

Главные площадки - площадки, на которых отсутствуют касательные напряжения. ()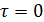

Главные напряжения - напряжения, действующие на главных площадках.

Пусть площадка главная, полное напряжение 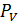совпадает с нормальными ()

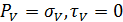Для главной площадки получим соотношение:

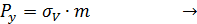
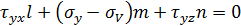
Неизвестными являются углы l,m,n. Дополнительным условием для нахождения этих соотношений является теорема косинусов.

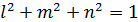
Из линейной алгебры следует, что система имеет решение если детерминант = 0.

Разворачиваем определитель, учитывая парность касательных напряжений:

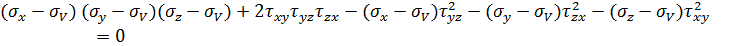
Путем сокращения получаем:

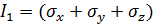
Корни полученного характеристического кубического уравнения напряженного состояния представляют собой величины главных напряжений 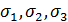. Для определения ориентации площадки, где действует в уравнение системы

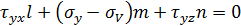
вносится значение вместо , далее определяются значения l,m,n с учетом теоремы косинусов, определяются l₁,m₁,n₁. Аналогично для 2 и 3.

Инварианты напряженного состояния в точке.

Расположение главных площадок и значение главных напряжений в точке тела зависит от действующих напряжений и не зависит от системы координат и ее изменения. Таким образом, коэффициенты характеристического уравнения напряженного состояния инвариантны к изменению системы координат. Инвариант - коэффициент характеристического уравнения напряженного состояния, не зависящий от системы координат.

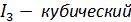
Тензор напряжений.

Напряженное состояние в точке тела описывают с помощью скалярных величин напряжений или 3 векторов, включающих 3 скалярные величины.

Величины, описываемые векторами, принято называть тензорами.

Тензор симметричен в силу парности касательных напряжений, что позволяет характеризовать его 6 скалярными величинами.

Date: 2015-08-15; view: 1179; Нарушение авторских прав