Технический оптимум при настройке регуляторов тока и скорости

Такая настройка применяется для систем второго порядка, ее называют также настройкой на технический оптимум. Термин обусловлен тем, что если характеристический полином системы второго порядка представить в канонической форме, т.е. в виде

(7.5) D (p)= T ₁² p ²+2ζ T ₁ p +1,то при 2ζ= 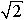обеспечивается переходный процесс, близкий к оптимальному, при котором будет небольшое перерегулирование и относительно высокое быстродействие.

Рассмотрим сначала простейшую систему, представленную в предыдущем пункте (двигатель питается от источника тока). В относительных единицах ее структурная схема представлена на рис. 7.3. Если коррекцию осуществлять путем подбора передаточной функции регулятора W _р(p), обеспечивающей оптимальный переходный процесс, то звенья с постоянными времени T _μ и T _о можно отнести к неизменной части системы, обозначив ее передаточную функцию через W _н(p). Учитывая введенное обозначение, запишем передаточную функцию разомкнутого контура

(7.6) W (p)= W _р(p) W _н(p),где

(7.7) ,

(7.8)

W _о(p) – передаточная функция объекта регулирования.В замкнутом состоянии привод будет описываться передаточной функцией

(7.9)

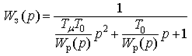Которая, в соответствии с нашим желанием обеспечить технический оптимум (7.5), за счет выбора передаточной функции регулятора W _р(p), должна быть приведена к следующему виду

(7.10)

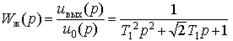Из условия тождественного равенства передаточных функций (7.9) и (7.10) справедливы соотношения для передаточной функции синтезируемого регулятора

(7.11) W _р(p)= T _μ T _о/ T ₁² и W _р(p)= T _о / ( 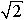T ₁),где T ₁ – свободная для выбора постоянная времени. Попробуем выбрать её так, чтобы компенсировать влияние большой постоянной времени T _о. Для этого введем подстановку T ₁= aT _μ и перепишем соотношения (7.11) в виде W _р(p)= T _о/(a ² T _μ) и W _р(p)= T _о / ( 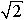aT _μ).

При a = 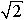, имеем

(7.12)

W _р(p)= T _о/(2 T _μ)= k _р.Такой регулятор называют пропорциональным (П-регулятором). Если прейти от относительных единиц к абсолютным, то согласно (7.3.в) получим

(7.13)

k _р= T _о/(2 T _μ k _п k _о k _ос).Таким образом, если передаточную функцию регулятора выбрать согласно (7.13), мы обеспечим настройку на оптимум по модулю и передаточная функция замкнутой системы, получит вид (7.10). Передаточную функцию настроенной на оптимум по модулю разомкнутой системы получим по выражению

(7.14)

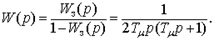Смысл термина настройки на оптимум по модулю в том, что при этом стремятся в широкой полосе частот сделать модуль частотной характеристики замкнутого контура близким к единице.Переходный процесс в системе при ступенчатом управляющем воздействии показан на рис. 7.5.а, кривая А. Выходная величина в первый раз достигает установившегося значения через время t =4.7 T _μ, перерегулирование составляет 4.3 %. Так как влияние постоянной времени объекта T _о было скомпенсировано коррекцией, длительность переходного процесса от нее не зависит, а определяется только малой постоянной времени T _μ.

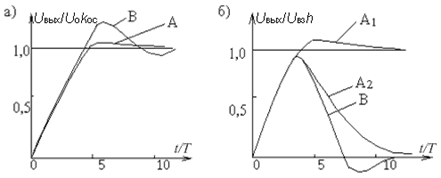
Рис. 7.5. Переходные процессы в приводе при различных настройках регулятора

Теперь предположим, что двигатель питается от преобразователя напряжения. В этом случае, в первом приближении, постоянную времени T _я можно не учитывать. Тогда передаточную функцию объекта по управлению можно представить в виде

(7.15) 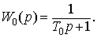Подставим W _о(p) из (7.15) в (7.7) и получим передаточную функцию разомкнутой системы

(7.16) 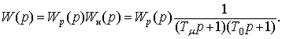Приравнивая правые части выражений (7.14) и (7.16), найдем передаточную функцию регулятора, при которой обеспечивается настройка системы на технический оптимум,

Учитывая полученное выше уравнение для оптимального передаточного коэффициента системы (7.13), представим полученную передаточную функцию стандартным пропорционально-интегральным звеном

(7.17) где τ_р= T _о, а k _р определяется по (7.13). Такой регулятор называют пропорционально-интегральным (ПИ-регулятор).Если двигатель питается от преобразователя напряжения, и мы учитываем постоянную времени якорной цепи, то согласно (2.35.а) передаточная функция объекта по управлению имеет вид

(7.18)

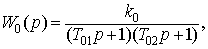где k _о=1/(K Φ), T _о1= T _м, T _о2= T _я.По аналогии с предыдущим случаем найдем

(7.19) 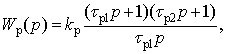где τ_р1= T _о1, τ_р2= T _о2, а k _р определяется по (7.13). Такой регулятор называют пропорционально интегрально дифференциальным (ПИД-регулятор).

Date: 2015-08-15; view: 6609; Нарушение авторских прав