
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Метод наименьших квадратов. При анализе результатов различных экспериментов очень часто возникает необходимость установить вид зависимости какой-либо величины y от величины х
|
|
При анализе результатов различных экспериментов очень часто возникает необходимость установить вид зависимости какой-либо величины y от величины х. Например, какова зависимость силы тока I в цепи от приложенного напряжения U или какова зависимость производительности труда работника от его заработной платы.
Чтобы установить вид функциональной зависимости y = f (x) производят ряд измерений искомой величины y для нескольких различных значений величины х.
Для наглядности результаты измерений, то есть экспериментальные точки с координатами (xi, yi), наносят на координатную плоскость OXY и пытаются подобрать функцию y = f (x), график которой наилучшим образом моделирует (отражает) реальную зависимость величины y от величины х. Этот метод называется аппроксимацией, а найденная приблѝженная к реальной функциональная зависимость – аппроксимирующей.
Существует множество методов нахождения аппроксимирующих зависимостей. Наиболее используемым является метод наименьших квадратов (МНК). Он базируется на следующих основных положениях:
1. Заранее на основании каких-либо предположений (например, на основании научных законов) выбирается общий вид зависимости y = f (x). Очень часто, и в естественных, и в социально-экономических науках в качестве аппроксимирующей выбирается линейнаязависимость у = ах + b.
Даже когда зависимость нелинейная (например, зависимость пути S от времени t при равноускоренном движении 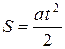 ), величины, откладываемые по координатным осям, выбирают таким образом, чтобы получить линейную зависимость. То есть, график пути S от времени t при равнопеременном движении строят в осях S = f (t 2). Тогда графиком является прямая линия, походящая через начало отсчёта.
), величины, откладываемые по координатным осям, выбирают таким образом, чтобы получить линейную зависимость. То есть, график пути S от времени t при равнопеременном движении строят в осях S = f (t 2). Тогда графиком является прямая линия, походящая через начало отсчёта.
2. Аппроксимирующая зависимость у = ах + b является оптимальной (наиболее приближенной к реальной), если сумма квадратов отклонений (расстояний) по вертикали от экспериментальных точек до кривой будет минимальной.
Для построения аппроксимирующей прямой y = ax + b необходимо найти значения углового коэффициента а и параметра b.
При выводе предположим, что погрешности содержат только величины yi (такое предположение часто оправдывается на практике), иначе вывод значительно усложнится. Пусть отклонение по вертикали экспериментального значения yi от аппроксимирующей прямой у = ах + b в i -ом (i = 1, 2, 3,..., n) измерении (при х = xi) равно
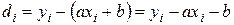 ,
,
тогда, согласно методу наименьших квадратов наилучшим приближением будет такая аппроксимирующая прямая, для которой сумма квадратов отклонений по вертикали от экспериментальных точек до прямой по всем n измерениям будет минимальной, т.е.
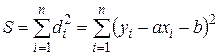 – минимальна.
– минимальна.
Для определения значений коэффициентов а и b аппроксимирующей прямой, при которых величина S будет минимальной, найдем частные производные  и
и 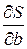 и приравняем их к нулю.
и приравняем их к нулю.
Составим систему уравнений:
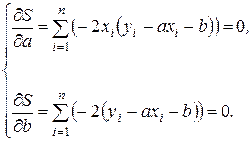 ; (3.2.1)
; (3.2.1)
Учитывая, что а = Const и b = Const, и, разделив каждое из уравнений системы (3.2.1) на 2, получим

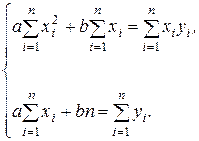 (3.2.2)
(3.2.2)
Коэффициенты а и b найдём решением системы уравнений (3.2.2).
Для нахождения коэффициента а, умножим первое уравнение системы (3.2.2) на n, а второе – на 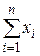 :
:
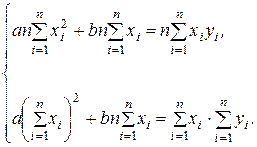 (3.2.3)
(3.2.3)
Вычтем второе уравнение системы (3.2.3) из первого и получим:
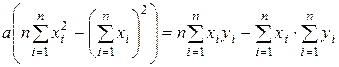 ,
,
откуда коэффициент а:
 . (3.2.4)
. (3.2.4)
Для нахождения коэффициента b, умножим первое уравнение системы (3.2.2) на 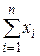 , а второе – на
, а второе – на 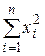 :
:
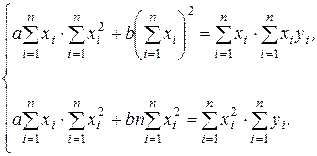 (3.2.5)
(3.2.5)
Вычтем первое уравнение системы (3.2.5) из второго и получим:
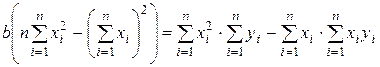 ,
,
откуда коэффициент b:
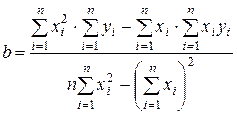 . (3.2.6)
. (3.2.6)
Очевидно, что ручная обработка результатов с помощью приведённых формул слишком трудоёмка. При построении графиков "вручную" метод наименьших квадратов используется интегрировано – прямая между экспериментальными точками проводится "на глаз".
3.2.2 Пример выполнения задания
Задача:
Экспериментально снята зависимость величины у от величины х (значения х и соответствующие им экспериментальные значения у приведены в таблице).
| x | ||||||||||
| y | 2,0 | 2,4 | 2,5 | 3,2 | 3,8 | 4,2 | 4,1 | 5,0 | 5,4 | 6,0 |
Методом наименьших квадратов определить коэффициенты а и b аппроксимирующей линейной зависимости у = ах + b. На системе координат OXY проставить экспериментальные точки и построить график аппроксимирующей зависимости.
Решение:
Коэффициенты а и b для построения аппроксимирующей линейной зависимости у = ax + b найдем методом наименьших квадратов, используя готовые формулы (3.2.4) и (3.2.6).
Для удобства вычислений заполним таблицу:
| i | 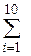
| 
| ||||||||||
| xi | ||||||||||||
| xi2 | – | |||||||||||
| yi | 2,0 | 2,4 | 2,5 | 3,2 | 3,8 | 4,2 | 4,1 | 5,0 | 5,4 | 6,0 | 38,8 | – |
| xiyi | 2,4 | 5,0 | 9,6 | 15,2 | 21,0 | 24,6 | 35,0 | 43,2 | 54,0 | – |
где
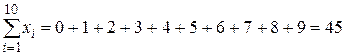 ;
;
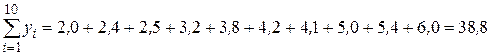 ;
;
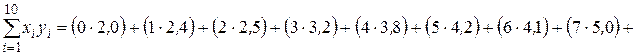
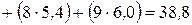 ;
;

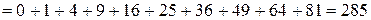 ;
;
 .
.
Тогда, учитывая, что число измерений n = 10, по формулам (3.2.4) и (3.2.6) найдём коэффициенты а и b аппроксимирующей линейной зависимости:
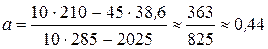 ;
;
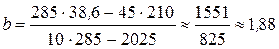 .
.
Следовательно, аппроксимирующая линейная зависимость имеет вид
у = 0,44 x + 1,88.
Для построения графика аппроксимирующей зависимости найдем координаты двух точек А и В, принадлежащих прямой:
| А | В | |
| x | ||
| y | 1,88 | 5,84 |
 На системе координат OXY проставим экспериментальные точки (обозначены символом «○») и построим график аппроксимирующей зависимости по точкам А и В (обозначены символом «*»).
На системе координат OXY проставим экспериментальные точки (обозначены символом «○») и построим график аппроксимирующей зависимости по точкам А и В (обозначены символом «*»).
Date: 2015-08-15; view: 1317; Нарушение авторских прав