Обработка результатов косвенных измерений

3.1.1 Краткие теоретические сведения

Косвенные измерения – это измерения, при которых искомая величина вычисляется по некоторой известной формуле на основе результатов прямых или косвенных измерений величин, связанных с искомой величиной определенной функциональной зависимостью и входящих формулу.

Алгоритм обработки результатов косвенных измерений

Пусть y - измеряемая величина, которая является функцией величин х ₁, х ₂, …, х_n, найденных в ходе n прямых измерений:

.

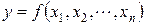Тогда для обработки результата косвенного измерения величины y необходимо:

1. Обработать результаты прямых измерений, задав некоторое значение доверительной вероятности α (например, α = 0,95) и представить их в виде доверительных интервалов:

х ₁ = (< х ₁> ± D х ₁);

х ₂ = (< х ₂> ± D х ₂);

…

х _n = (< х _n> ± D х_n).

2. Рассчитать среднее значение величины < y > как функцию величин < x ₁>, < x ₂>,..., < x_n >:

.

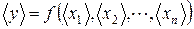3. Рассчитать полуширину доверительного интервала D y по формуле (число слагаемых в формуле равно числу переменных):

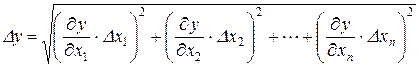, (3.1.1)

где 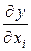- частная производная функции 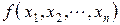по переменной х_i.

В формулу 3.1.1 подставляют значения частных производных, найденные при подстановке средних значений переменных .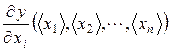

4. Записать результат измерений в виде доверительного интервала

y = (< y > ± D y) ед. изм., a = 0,95.

5. Указать относительную погрешность

.

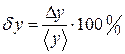3.1.2 Пример выполнения задания

Задача:

Проводник длиной ℓ = (60,0 ± 0,1) м и площадью сечения S = (0,34 ± 0,01) мм ² имеет сопротивление R = 3,0 Ом, определённое с относительной погрешностью δR = 2%. Определить (с учётом погрешности) удельное сопротивление проводника.

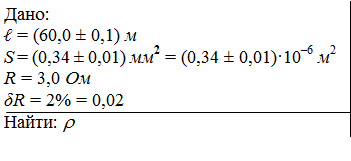Решение:

Удельное сопротивление проводника рассчитывается по формуле

,

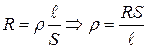т.е. измеряемая величина r является функцией трёх переменных R, S и ℓ

r = f (R, S, ℓ).

Для решения задачи воспользуемся алгоритмом обработки результатов косвенных измерений.

1. Обработаем результаты прямых измерений. Из условия задачи следует, что

< ℓ > = 60,0 м; D ℓ = 0,1 м;

< S > = 0,34·10^–6 м ²; D S = 0,01·10^–6 м ²;

<R> = 3,0 Ом; 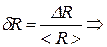D R = < R >· δR = 3,0 Ом ·0,02 = 0,06 Ом.

2. Найдем среднее значение величины < r > по формуле:

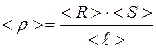
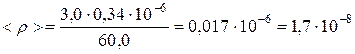(Ом·м).

3. Найдём полуширину доверительного интервала Δ r по формуле:

.

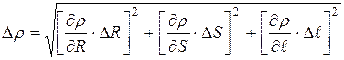Для этого найдём значения частных производных функции < r > при средних значениях величин <R>, < S >, < ℓ >:

; ; .

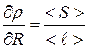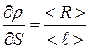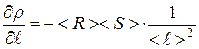Тогда

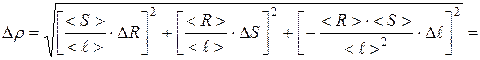
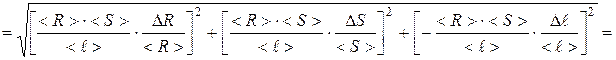
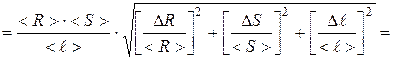
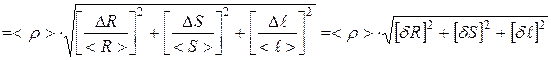
где d R, d S, d ℓ – относительные погрешности.

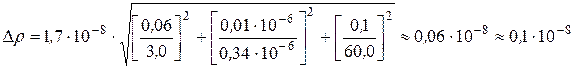(Ом·м).

4. Запишем результат измерения:

r = (1,7 ± 0,1)·10^–8 Ом·м, a = 0,95.

5. Укажем относительную погрешность

; .

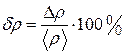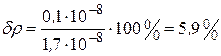Date: 2015-08-15; view: 7120; Нарушение авторских прав