Кинематические диаграммы движения ползуна

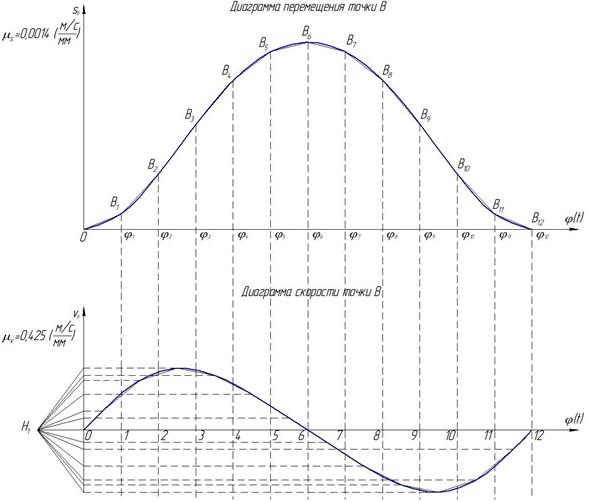
Сначала строим диаграмму перемещений ползуна 3. По оси ординат будем откладывать перемещения ползуна S, а по оси абсцисс – угол поворота кривошипа , или время t (рис. 6.26).

Рис.6.26. Диаграммы перемещений (а) и скоростей (б) см. ползуна

На оси абсцисс от начала координат откладываем отрезок длиной 225 мм, который соответствует углу полного оборота кривошипа и времени одного полного оборота кривошипа. Разбиваем этот отрезок на 12 равных частей и через полученные точки проводим вертикальные линии.

На планах положений механизма (см. рис. 6.22) за начальную точку отсчета перемещений ползуна берем точку В_о. Принимаем масштаб перемещений ползуна по оси ординат (рис. 6.26, а) равным по величине масштабу длин планов положений механизма: 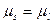=0,0014 ().

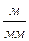Благодаря этому перемещения ползуна В₀В₁, В₀В₂, В₀В₃ и другие перемещения, измеренные на планах положений механизма, можно без изменений откладывать по вертикалям из точек 1, 2, 3 и так далее на оси абсцисс диаграммы перемещений ползуна (см. рис. 6.26,а). Обведя найденные точки плавной кривой, получаем искомую диаграмму.

Масштаб углов поворота кривошипа

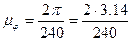=0,026 ().

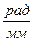Время одного полного оборота кривошипа

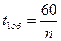= =0,0316 ().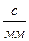

Масштаб времени

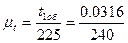=0,0001317 ().

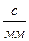Графически дифференцируя диаграмму перемещений ползуна методом хорд, получаем диаграмму скоростей ползуна (см. рис. 6.26). Для этого на диаграмме перемещений проводим хорды 0-В₁^', В₁^’- В₂ и так далее. Ось абсцисс диаграммы скоростей продолжаем от начала координат влево и откладываем от точки 0 полюсное расстояние H₁= 25 мм. Из полученной точки полюса проводим лучи, параллельные этим хордам. Каждую точку пересечения луча с осью скоростей переносим на вертикаль, проведенную через середину того интервала оси абсцисс, на котором проводилась соответствующая хорда диаграммы перемещений. Обведя найденные точки плавной кривой, получаем диаграмму скоростей ползуна.

Масштаб по оси ординат диаграммы скоростей:

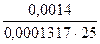= =0,425 ().

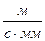Графически дифференцируя диаграмму скоростей ползуна (рис. 6.27, а) методом хорд, получаем диаграмму ускорений ползуна (рис. 6.27, б). Графическое дифференцирование выполняем в той же последовательности.

Принимаем полюсное расстояние H₂=25 мм. Масштаб по оси ординат диаграммы ускорений:

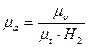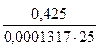= =129,11 ().

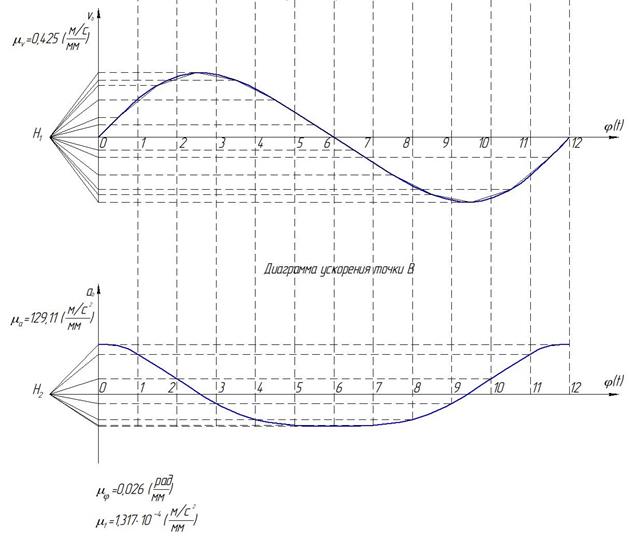
Рис. 6.27. Диаграммы скоростей (а) и ускорений (б) ползуна

Планы скоростей механизма

Строим 12 планов скоростей для каждого из 12 положений механизма.

Вычисляем угловую скорость входного звена 1:

().

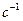Строим, например, план скоростей механизма (рис. 6.28, б) для положения механизма №4 (рис. 6.28, а).

Рис. 6.28. Кинематическая схема кривошипно-ползунного механизма

двигателя(а) и план скоростей (б)

Рассматриваем вначале скорости точек входного звена ОА. Скорость точки О равна нулю, так как эта точка неподвижна при работе механизма: 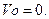Вектор скорости 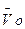на плане скоростей поэтому отсутствует; точка о на плане скоростей совпадает с полюсом р.

Для определения скорости точки А составляем векторное уравнение скоростей: 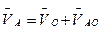. Так как 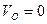, то .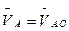

Определяем величину этой скорости:

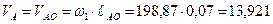
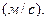
Вектор 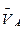(см. рис. 6.28, б) перпендикулярен линии АО звена на схеме механизма и направлен в сторону заданной угловой скорости этого звена. Задаемся длиной этого вектора и проводим этот вектор. Принимаем 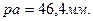Тогда масштаб плана скоростей будет

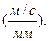
Для определения скорости точки В составляем систему двух векторных уравнений скоростей:

,

.

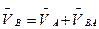Приравниваем правые части этих двух уравнений, так как левые части их равны:

.

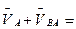
В уравнении точка В₆ - это неподвижная точка стойки 6, которая в рассматриваемое мгновение совпадает по положению с подвижной точкой В ползуна 3.

Так как 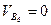, то полученное уравнение можно представить в виде

.

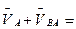
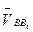В этом уравнении абсолютная скорость 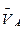уже известна, а скорости в относительном движении точек 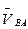и 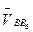известны только по направлению. Так как точки В и А принадлежат одному и тому же звену 2, то 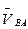перпендикулярна прямой линии ВА схемы механизма. Так как точки В и В₆ совпадают по положению и принадлежат разным звеньям, входящим в поступательную пару, то 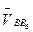параллельна направляющей относительного поступательного движения звеньев 3 и 6, то есть параллельна линии ОВ механизма (см. рис. 6.28, а).

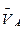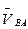В соответствии с уравнением из конца вектора скорости - точки (см. рис.6.28, б) - проводим линию вектора скорости перпендикулярно прямой линии ВА схемы механизма. Из точки 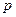полюса плана скоростей проводим линию вектора 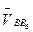параллельно направляющей относительного поступательного движения звеньев 3 и 6, то есть параллельно линии ОВ механизма. Находим точку пересечения этих двух линий. Это точка плана скоростей.

Для определения скорости точки С составляем систему двух векторных уравнений скоростей: ,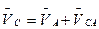

.

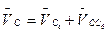Приравниваем правые части этих двух уравнений, так как левые части их равны:

.

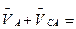
В уравнении точка С₆ - это неподвижная точка стойки 6, которая в рассматриваемое мгновение совпадает по положению с подвижной точкой С ползуна 5.

Так как , то полученное уравнение можно представить в виде

.

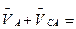
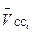В этом уравнении абсолютная скорость 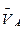уже известна, а скорости в относительном движении точек 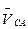и 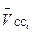известны только по направлению. Так как точки С и А принадлежат одному и тому же звену 4, то 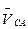перпендикулярна прямой линии СА схемы механизма. Так как точки С и С₆ совпадают по положению и принадлежат разным звеньям, входящим в поступательную пару, то 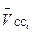параллельна направляющей относительного поступательного движения звеньев 5 и 6, то есть параллельна линии ОС механизма (см. рис. 6.28, а).

В соответствии с уравнением из конца вектора скорости 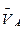- точки (см. рис. 6.28, б) - проводим линию вектора скорости 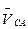перпендикулярно прямой линии СА схемы механизма. Из точки 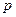полюса плана скоростей проводим линию вектора 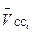параллельно направляющей относительного поступательного движения звеньев 5 и 6, то есть параллельно линии ОС механизма. Находим точку пересечения этих двух линий. Это точка 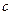плана скоростей.

Аналогично строятся планы скоростей для других положений механизма.

Планы ускорений механизма

Необходимо построить планы ускорений кривошипно-ползунного механизма лишь для двух цилиндров двигателя внутреннего сгорания (рис. 6.29, а).

Строим план ускорений для того положения механизма, для которого по заданию дано значение угла =120^о поворота кривошипа, то есть для четвертого положения механизма.

Рассматриваем вначале ускорения точек входного звена АО. Ускорение точки О равно нулю, так как эта точка неподвижна при работе механизма: 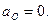На плане ускорений вектор 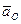поэтому отсутствует; точка на плане ускорений совпадает с полюсом (см. рис.6.29, б).

Рис. 6.29. Кинематическая схема кривошипно-ползунного механизма двигателя (а)

и план ускорений (б)

Для определения ускорения точки А составляем векторное уравнение ускорений:

.

Величину тангенциальной составляющей ускорения определяем по формуле

,

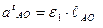где 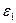– угловое ускорение звена 1, на котором расположены рассматриваемые точки, 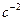; 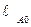– расстояние между точками А и О, м.

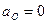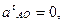По заданию вращение входного звена механизма (кривошипа АО) равномерное, поэтому тангенциальная составляющая ускорения точки А относительно точки О равна нулю. Так как и то .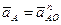

Величину этого ускорения определяем по формуле

.

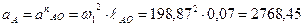
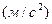Вектор 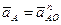(см. рис. 6.29, б) параллелен линии АО звена 1 на схеме механизма (см. рис. 6.29, а) и направлен от точки А, движение которой рассматривается, к точке О, принятой в качестве полюса. Задаемся длиной этого вектора и проводим этот вектор. Принимаем 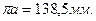Тогда масштаб плана ускорений будет

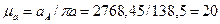
Рассматриваем далее точки структурной группы звеньев 2-3: А, В и В₆.

В поступательной кинематической паре соединения звеньев 3 и 6 взяты две точки: подвижная точка В, принадлежащая звену 3, и неподвижная точка В₆, принадлежащая звену 6 (стойке). Обе эти точки в рассматриваемое мгновение по положению совпадают.

Ускорение точки В необходимо определить. Ускорения же двух остальных точек известны: ускорение точки А найдено, и его вектор на плане ускорений уже проведен, ускорение же точки В₆ стойки равно нулю.

Составляем систему двух векторных уравнений ускорений:

;

.

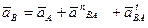Приравниваем правые части этих двух уравнений, так как левые части их равны:

.

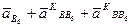Вычисляя кориолисово ускорение, видим, что оно равно нулю, так как ползун 3 и направляющая стойки 6, входящие в поступательную кинематическую пару, вращательного движения совершать не могут:

Так как 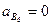и , то векторное уравнение для ускорений точек механизма можно представить в виде .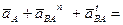

Определяем величину и направление нормальной составляющей ускорения :

,

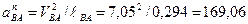
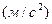где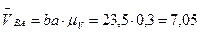

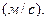
Вектор 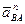(см. рис. 6.29, б) параллелен линии BА звена на схеме механизма и направлен от точки В, движение которой рассматривается, к точке А, принятой в качестве полюса.

Так как по уравнению эту составляющую необходимо прибавить к ускорению 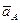, то на плане ускорений точка на конце вектора 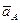будет началом вектора 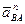. Определяем длину этого вектора с учетом принятого масштаба плана ускорений:

().

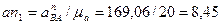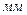Проводим этот вектор. По уравнению необходимо далее прибавить вектор тангенциальной составляющей ускорения 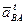, поэтому из точки 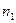плана ускорений (см. рис. 6.29, б) проводим линию вектора 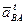. Направление этого вектора известно: он перпендикулярен прямой ВА схемы механизма, а величину вычислить не представляется возможным, так как угловое ускорение звена АВ неизвестно.

По уравнению на плане ускорений необходимо провести еще релятивное ускорение , направление которого известно: оно параллельно направляющей относительного поступательного движения звеньев 3 и 6, то есть параллельно линии ОВ механизма (см. рис. 6.29, а). Величина вектора неизвестна.

Из полюса плана ускорений (см. рис. 6.29, б) проводим линию вектора параллельно направляющей относительного поступательного движения звеньев 3 и 6, то есть параллельно линии ОВ механизма. Находим точку пересечения этой линии с линией вектора 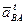. Это точка плана ускорений. В соответствии с уравнением обозначаем стрелки векторов ускорений на плане ускорений.

Находим положение точек s₂ и s₃ центров тяжести шатуна 2 и ползуна 3 на плане ускорений. Считаем, что точки В и S₃ у механизма совпадают. Аналогичные точки должны совпадать и на плане ускорений. По заданию имеем следующее соотношение размеров длин на схеме механизма:

AS₂/AB=0,26.

По теореме подобия для планов ускорений аналогичное соотношение соответствующих размеров должно быть и на плане ускорений. Отсюда

().

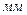Откладывая это расстояние на плане ускорений, получаем точку s₂. Соединяя точку полюса плана ускорений с найденной точкой s₂, получаем вектор ускорения точки S₂.

Ускорения центров тяжести шатуна и ползуна:

,

.

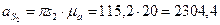
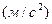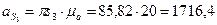
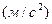Рассматриваем далее точки структурной группы звеньев 4-5: А, С и С₆. В поступательной кинематической паре соединения звеньев 5 и 6 взяты две точки: подвижная точка С, принадлежащая звену 5, и неподвижная точка С₆, принадлежащая звену 6 (стойке). Обе эти точки в рассматриваемое мгновение по положению совпадают.

Ускорение точки С необходимо определить. Ускорения же двух остальных точек известны: ускорение точки А найдено, и его вектор на плане ускорений уже проведен, ускорение же точки С₆ стойки равно нулю. Составляем систему двух векторных уравнений ускорений:

;

.

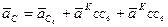Приравниваем правые части этих двух уравнений, так как левые части их равны:

.

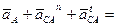
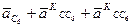Вычисляя кориолисово ускорение, видим, что оно равно нулю, так как ползун 5 и направляющая стойки 6, входящие в поступательную кинематическую пару, вращательного движения совершать не могут: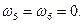

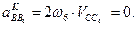
Так как 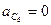и , то векторное уравнение для ускорений точек механизма можно представить в виде

.

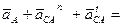
Определяем величину и направление нормальной составляющей ускорения : (),

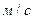где ().

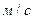Вектор (см. рис. 6.29, б) параллелен линии СА звена на схеме механизма (см. рис. 6.29, а) и направлен от точки С, движение которой рассматривается, к точке А, принятой в качестве полюса.

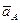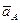Так как по уравнению эту составляющую необходимо прибавить к ускорению , то на плане ускорений точка на конце вектора будет началом вектора . Определяем длину этого вектора с учетом принятого масштаба плана ускорений:

().

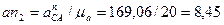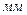Проводим этот вектор. По уравнению необходимо далее прибавить вектор тангенциальной составляющей ускорения 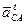, поэтому из точки плана ускорений (см. рис. 6.29,б) проводим линию вектора 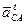. Направление этого вектора известно: он перпендикулярен прямой СА схемы механизма, а величину вычислить не представляется возможным, так как угловое ускорение звена АС неизвестно.

По уравнению на плане ускорений необходимо провести еще релятивное ускорение 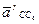, направление которого известно: оно параллельно направляющей относительного поступательного движения звеньев 5 и 6, то есть параллельно линии ОС механизма (см. рис. 6.29, б). Величина вектора неизвестна.

Из полюса плана ускорений проводим линию вектора параллельно направляющей относительного поступательного движения звеньев 5 и 6, то есть параллельно линии ОС механизма. Находим точку пересечения этой линии с линией вектора 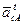. Это точка 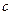плана ускорений. В соответствии с уравнением показываем стрелки векторов ускорений на плане ускорений.

Находим положение точек s₄ и s₅ центров тяжести шатуна 4 и ползуна 5 на плане ускорений. Считаем, что точки С и S₅ у механизма совпадают. Аналогичные точки должны совпадать и на плане ускорений. По заданию имеем следующее соотношение размеров:

AS₄/AС=0,26.

По теореме подобия для планов ускорений аналогичное соотношение соответствующих размеров должно быть и на плане ускорений. Отсюда

().

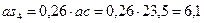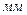Откладывая это расстояние на плане ускорений, получаем точку s₄. Соединяя точку полюса плана ускорений с найденной точкой s₄, получаем вектор ускорения точки S_4й.

Ускорения центров тяжести шатуна и ползуна:

,

.

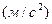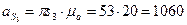
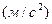На рис. П.6 приведен вид первого листа курсового проекта.

Date: 2015-08-15; view: 5404; Нарушение авторских прав