
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Цилиндрических зубчатых колес
|
|
Необходимо построить зацепление двух эвольвентных зубчатых колес. Даны числа зубьев двух колес и модуль: Z1= 16, Z2= 36, m=4,5.
Передаточное отношение этой передачи u12 = Z2 / Z1 = 36/16 = 2,25.
Для уменьшения габаритов зубчатых передач колеса следует проектировать с малым числом зубьев. Однако при числе зубьев меньшем 17 имеет место подрезание ножек зубьев зуборезным инструментом, что уменьшает эвольвентную часть профилей зубьев и ослабляет зубья в их опасных сечениях.
Чтобы не происходило подрезание, нарезание зубьев колес производят при положительном смещении инструмента по отношении к заготовке колеса. Инструмент отодвигают от центра заготовки колеса. Величины сдвига инструмента при нарезании первого и второго колеса зубчатой передачи не равны, зависят от сочетания числа зубьев колес и определяются значениями коэффициентов Х1 и Х2 смещения инструмента. Значения коэффициентов смещения инструмента Х1 и Х2, а также коэффициента обратного смещения 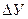 принимаются по таблицам 3.1, 3.2, 3.3, 3.4 или [3, табл. 3, 4, 5, 6] в зависимости от передаточного числа передачи u = Z2 / Z1.
принимаются по таблицам 3.1, 3.2, 3.3, 3.4 или [3, табл. 3, 4, 5, 6] в зависимости от передаточного числа передачи u = Z2 / Z1.
Таблица 3.1
Значения коэффициентов Х1 и Х2 для неравносмещенного внешнего
зацепления при 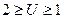
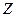 2 2
| Значения при 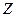 1 1
| |||||||||||
| Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | Х1 | Х2 | |
| 0,395 0,432 0,464 0,490 0,513 0,534 0,551 0,568 0,584 0,601 0,617 0,630 - - - - - - - - - - | 0,395 0,372 0,354 0,341 0,330 0,322 0,317 0,312 0,308 0,303 0,299 0,297 - - - - - - - - - - | - 0,444 0,479 0,515 0,543 0,566 0,589 0,609 0,626 0,646 0,663 0,679 0,693 0,706 - - - - - - - - | - 0,444 0,423 0,400 0,386 0,376 0,365 0,358 ,353 0,345 0,341 0,337 0,334 0,333 - - - - - - - - | - - 0,486 0,524 0,557 0,588 0,614 0,636 0,659 0,676 0,694 0,714 0,730 0,745 0,758 0,773 - - - - - - | - - 0,486 0,462 0,443 0,426 0,414 0,405 0,394 0,389 0,384 0,376 0,372 0,369 0,368 0,365 - - - - - - | -- - - 0,525 0,565 0,600 0,631 0,661 0,686 0,706 0,726 0,745 0,763 0,780 0,796 0,813 0,826 0,840 - - - - | -- - - 0,525 0,506 0,485 0,468 0,452 0,441 0,433 0,426 0,419 0,414 0,409 0,405 0,400 0,399 0,397 - - - - | -- - - - 0,571 0,609 0,644 0,677 0,706 0,731 0,754 0,775 0,792 0,813 0,830 0,848 0,862 0,881 0,894 0,908- - | - - - - 0,571 0,547 0,526 0,508 0,492 0,481 0,472 0,463 0,458 0,449 0,445 0,440 0,438 0,431 0,430 0,428 - - | -- - - - - 0,608 0,644 0,678 0,716 0,744 0,766 0,793 0,815 0,834 0,854 0,869 0,892 0,907 0,921 0,936 0,951 0,967 | - - - - - 0,608 0,586 0,566 0,542 0,528 0,519 0,507 0,497 0,491 0,483 0,480 0,470 0,4670,465 0,462 0,459 0,455 |
Таблица 3.2
Значения коэффициента 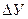 для неравносмещенного внешнего
для неравносмещенного внешнего
зацепления при 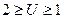
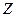 1 1
| ||||||
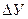
| 0,127 | 0,145 | 0,160 | 0,175 | 0,19 | 0,202 |
Таблица 3.3
Значения коэффициентов 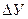 и Х1 для неравносмещенного внешнего
и Х1 для неравносмещенного внешнего
зацепления при 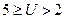
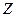 1 1
| ||||||
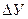 Х1
Х1
| 0,16 0,66 | 0,17 0,73 | 0,18 0,80 | 0,19 0,86 | 0,20 0,92 | 0,21 0,98 |
Таблица 3.4
Значения коэффициентов Х2 для неравносмещенного внешнего
зацепления при 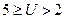
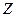 2 2
| Значение при 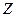 1 1
| |||||
| 0,442 0,501 0,556 0,610 0,661 0,709 0,754 - - - - - | 0,425 0,486 0,542 0,596 0,648 0,696 0,745 0,789 - - - - | - 0,471 0,528 0,582 0,635 0,685 0,734 0,782 0,822 - - - | - 0,463 0,522 0,577 0,632 0,684 0,732 0,780 0,825 0,866 - - | - - 0,518 0,575 0,628 0,682 0,731 0,779 0,826 0,870 0,909 - | - - 0,512 0,569 0,624 0,677 0,728 0,778 0,827 0,872 0,914 0,954 |
При курсовом проектировании расчет геометрических параметров неравносмещенной цилиндрической прямозубой передачи внешнего зацепления студенты выполняют на компьютере по программе, подготовленной на кафедре строительной техники и инженерной механики ВГАСУ.
Расчет начинают с определения через заданный модуль передачи шага 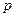 по формуле (3.3). Принимают согласно стандарту значение коэффициента высоты зуба
по формуле (3.3). Принимают согласно стандарту значение коэффициента высоты зуба 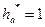 и значение коэффициента радиального зазора
и значение коэффициента радиального зазора 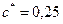 .
.
Остальные параметры передачи определяются следующим образом:
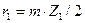 ; (3.22)
; (3.22)
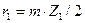 ; (3.23)
; (3.23)
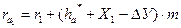 ; (3.24)
; (3.24)
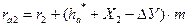 ; (3.25)
; (3.25)
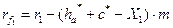 ; (3.26)
; (3.26)
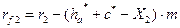 ; (3.27)
; (3.27)
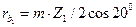 ; (3.28)
; (3.28)
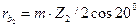 ; (3.29)
; (3.29)
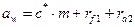 ; (3.30)
; (3.30)
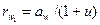 ; (3.31)
; (3.31)
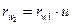 ; (3.32)
; (3.32)
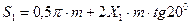 ; (3.33)
; (3.33)
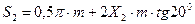 ; (3.34)
; (3.34)
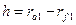 . (3.35)
. (3.35)
При построении зацепления зубчатых колес следует показать по три зуба каждого колеса. Высоту зуба на чертеже необходимо принять равной 50 мм. Тогда масштаб длин вычисляют следующим образом: 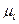 =
= 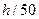
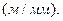
По табл. 3.3 и 3.4 при 5> u12 > 2 для неравносмещенного внешнего зацепления находим коэффициенты смещения инструмента X1 и X2, а также коэффициент обратного смещения 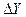 .
.
По табл. 3.3 при Z1= 16 имеем: X1= 0,98; 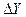 =0,21.
=0,21.
По табл. 3.4 при Z1= 16 имеем: для Z2= 35 X2=0,512, для Z2= 40 X2=0,569.
Вычисляем значение коэффициента смещения инструмента X2, соответствующего заданному значению числа зубьев колеса Z2= 36:
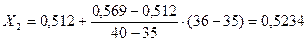 .
.
Геометрические параметры зубчатых колес вычисляем на компьютере по программе, подготовленной на кафедре строительной техники и инженерной механики Воронежского ГАСУ. Результаты расчета представлены на рис. 6.15.
Расчет выполнялся по формулам (3.22)….(3.31).
По программе расчета для построения зацепления зубчатых колес подобран такой масштаб длин, чтобы полная высота зубьев на картине зацепления была равна 50 мм. Для выполнения построения в этом масштабе 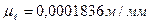 каждый параметр зубчатого зацепления поделен на выбранный масштаб длин (см. рис. 6.15).
каждый параметр зубчатого зацепления поделен на выбранный масштаб длин (см. рис. 6.15).
Откладываем вначале межцентровое расстояние О1О2 зацепления (рис. 6.16). Точка О2 выходит за пределы габаритных размеров чертежной бумаги, поэтому приходится приклеивать дополнительный листок бумаги необходимых размеров.
Проводим основные окружности колес радиусами rb1 и rb2 и общую касательную NN к этим окружностям. Эта линия NN является линией зацепления зубчатых колес, на которой располагаются точки касания зубьев. Находим теоретический участок КL линии зацепления, расположенный между точками касания этой линии с основными окружностями колес. Обозначаем точку P пересечения линии зацепления NN c линией межцентрового расстояния О1О2. Эта точка P называется полюсом зацепления.
Далее путем перекатывания без скольжения прямой NN по основной окружности первого колеса строим эвольвенту бокового профиля зуба этого колеса так, чтобы она проходила через полюс зацепления зубьев P (рис. 6.17).
Для этого отрезок РК делим на четыре равных интервала. От точки К по дуге основной окружности (см рис 6.17) откладываем хорды К-1’, 1’-2’,
2’-3’ и 3’-4’. Через полученные точки 1’, 2’, и 3’ проводим касательные к основной окружности зубчатого колеса. Эти касательные определяют положение прямой линии, перекатываемой без скольжения по основной окружности зубчатого колеса. Откладываем по касательным вправо: от точки 1’ – отрезок длиной в три интервала, от точки 2’ – отрезок длиной в два интервала и от точки 3’ – отрезок длиной в один интервал. Полученные точки являются точками эвольвентного бокового профиля зубчатого колеса. Эти точки обводим плавной кривой, называемой эвольвентой. Соединяем эти точки с полюсом Р и корнем эвольвенты – точкой 4.


Рис. 6.15. Результаты расчета на компьютере геометрических параметров неравносмещенной эвольвентной зубчатой передачи


Рис. 6.16. Построение линии зацепления эвольвентной зубчатой передачи
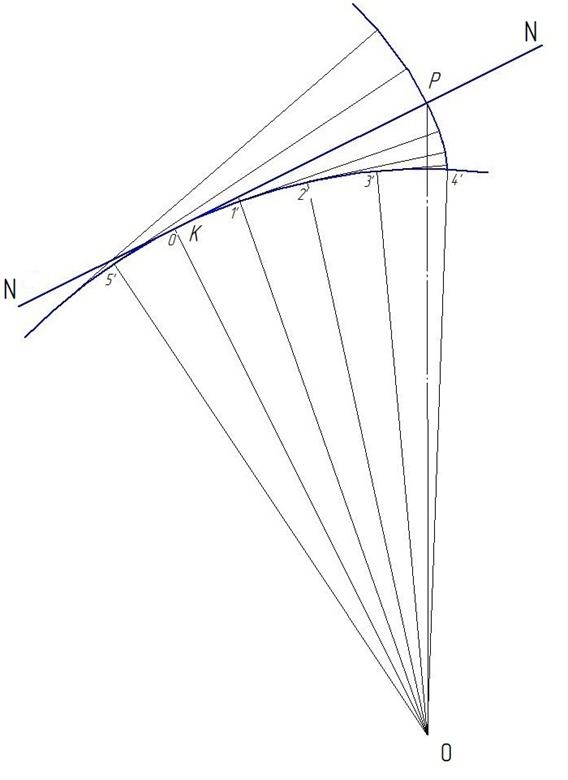
Рис. 6.17. Построение эвольвенты бокового профиля зуба колеса
Перекатывая прямую РК по основной окружности в противоположном направлении, строим эвольвенту зуба до окружности выступов колеса.
Проводим окружности выступов и впадин первого колеса радиусами ra1 и rf1 (рис. 6.18). У основания зуб имеет закругление радиусом
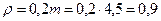
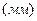
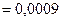
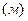 .
.

Рис. 6.18. Построение эвольвентного бокового профиля зуба первого колеса
Выполняем закругление у основания зуба радиусом, который с учетом масштаба построения равен
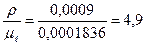
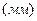 .
.
Проводим делительную окружность первого зубчатого колеса радиусом r1 (см. рис. 6.18). От точки пересечения делительной окружности с эвольвентой бокового профиля зуба откладываем влево половину толщины зуба по делительной окружности первого колеса S1/2. Через полученную точку проводим штрихпунктирной линией радиальную прямую, проходящую через центр колеса 1. Эта линия является осью симметрии зуба колеса 1.
Правая половина зуба уже построена. Для построения симметричной левой половины этого зуба изготавливаем шаблон: тонкий лист бумаги накладываем на построенную левую половину зуба, обводим просвечиваемый через бумагу контур половины зуба, затем вырезаем этот контур ножницами. Шаблон переворачиваем, совмещаем его прямолинейную часть с осевой штрихпунктирной линией зуба и обводим эвольвентный левый боковой профиль зуба (см. рис. 6.18).
Строим далее профили соседних зубьев колеса 1, расположенных слева и справа от построенного профиля зуба (рис. 6.19).

Рис. 6.19. Построение смежных левого и правого зубьев колеса
Для этого от точки построенного зуба, лежащей на пересечении оси симметрии зуба и делительной окружности, откладываем влево и вправо шаг 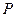 зубчатого зацепления по делительной окружности. Для повышения точности построения шаг откладываем как сумму трех одинаковых хорд. Через полученные точки проводим штрихпунктирными линиями оси симметрии смежных зубьев. Используя имеющийся шаблон, проводим боковые эвольвентные профили соседних зубьев.
зубчатого зацепления по делительной окружности. Для повышения точности построения шаг откладываем как сумму трех одинаковых хорд. Через полученные точки проводим штрихпунктирными линиями оси симметрии смежных зубьев. Используя имеющийся шаблон, проводим боковые эвольвентные профили соседних зубьев.
Профили трех зубьев зубчатого колеса 2 строим в аналогичной последовательности.
Находим точки А и В пересечения окружностей выступов колес с линией зацепления NN (рис. 6.20).
Участок АВ называется практическим участком линии зацепления.



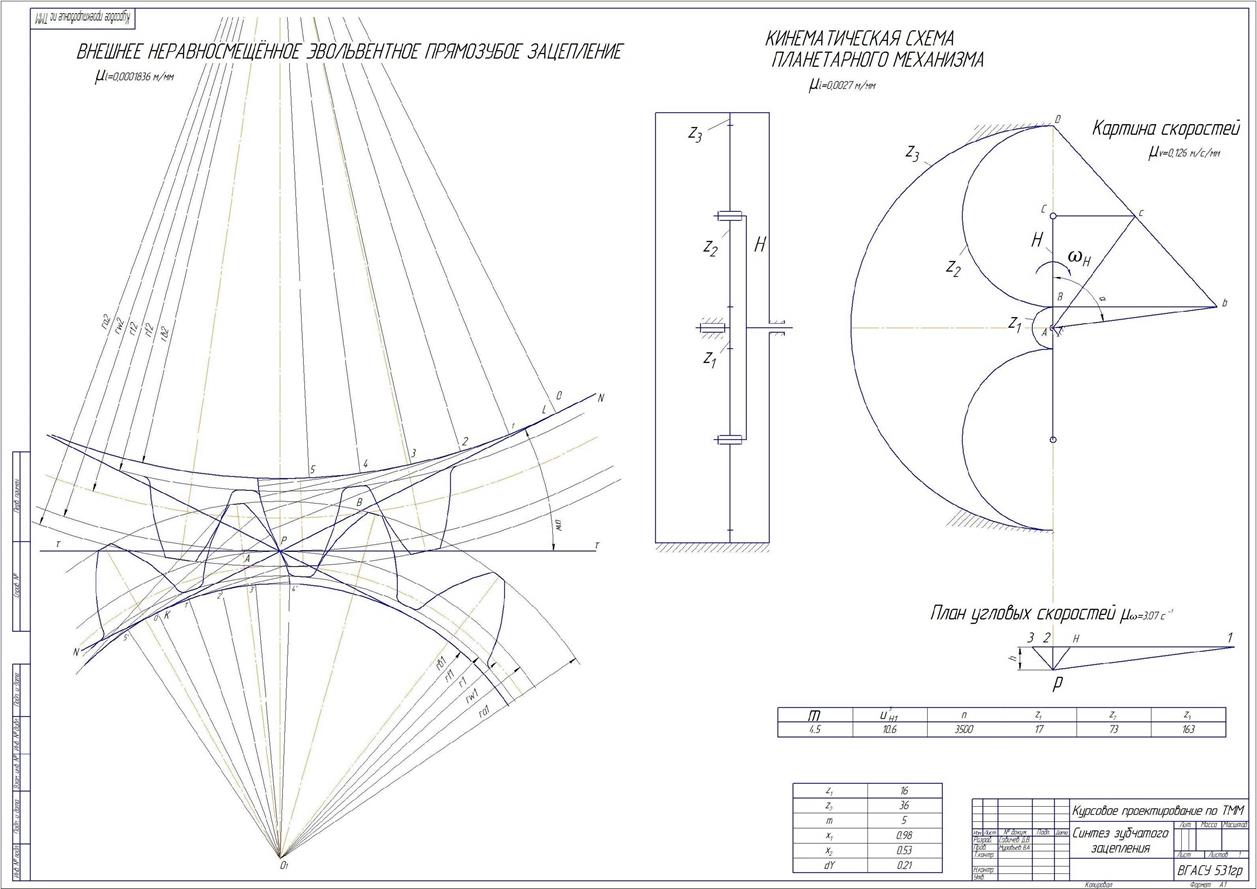
Рис. 6.20. Сопряжение зубьев колес внешней неравносмещенной прямозубой цилиндрической передачи
Для проектируемой планетарной зубчатой передачи общее передаточное отношение выражается через количество зубьев колес по формуле

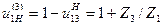 .
.
Находим отсюда число зубьев 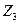 центрального неподвижного зубчатого колеса с внутренними зубьями:
центрального неподвижного зубчатого колеса с внутренними зубьями:
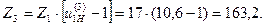
Проверяем, правильно ли выполнено построение зацепления зубьев колес: касание боковых профилей зубьев возможно лишь на практическом участке АВ линии зацепления. При вращении колес в противоположном направлении линия зацепления, являющаяся общей касательной к основным окружностям колес, будет располагаться симметрично обозначенной линии NN. Проводим эту линию (см. рис. 6.20).
Находим на этой линии участок симметричный практическому участку линии зацепления АВ. Касание боковых профилей зубьев возможно и на этом участке. Если имеется касание зубьев не на линиях зацепления, то необходимо вносить исправления в построении зацепления.
Синтез планетарной зубчатой передачи
Date: 2015-08-15; view: 619; Нарушение авторских прав