Методические указания по решению задач

Решать задачи с применением законов динамики целесообразно следующим образом.

1) Выбрать систему отсчета - инерциальную или неинерциальную.

2) Установить, каким моделям объектов и движений соответствует физическая ситуация, описанная в условии задачи. Сделать рисунок.

3) Назвать все силы, действующие на каждое тело, указывая их происхождение. Изобразить силы на рисунке. Записать законы сил.

4) Записать законы динамики в векторной форме.

5) Выбрать и изобразить на рисунке оси координат. Ось х удобно направить по вектору ускорения. Можно для всех тел указать общую систему координат, иногда удобно каждому телу сопоставить свою систему.

6) Записать систему динамических уравнений в проекциях на оси координат.

7) Установить уравнения кинематической связи.

8) Проверить, является ли система уравнений полной, решить ее в общем виде.

9) Проанализировать полученный результат.

Примечание: при решении некоторых задач выполняются не все пункты алгоритма.

Пример 1. При движении автомобиля с постоянным ускорением 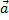, маятник (материальная точка подвешенная на нити) отклоняется от вертикали на угол 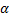(рис.8). Определим с каким ускорением движется автомобиль и натяжение нити.

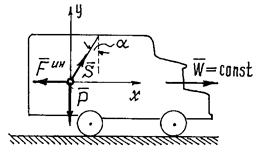
Рис.8

Рассмотрим «динамическое равновесие» точки. Его так называют потому, что на самом деле точка не находится в равновесии, она движется с ускорением.

На точку действуют силы: вес 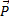и натяжение нити 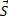, реакция нити. Приложим к точке ее силу инерции , направленную в сторону противоположную ускорению точки и автомобиля, и составим уравнение равновесия:

;

.

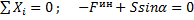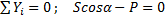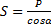
Из первого и .

Пример 2. Лифт весом Р (рис.9) начинает подниматься с ускоре­нием a. Определить натяжение троса.

Рис. 9

Рассматривая лифт как свободный, заменяем действие связи (троса) реакцией Т и, составляя уравнение в проекции на вертикаль, получаем:

Отсюда находим:

Если лифт начнёт опускаться с таким же ускорением, то натяжение троса будет равно:

Пример 3. Тело массой 300 кг лежит на полу кабины грузового подъемника, поднимающегося вверх (рис.10). Дано: m=300 кг, а=3 м/с² – ускорение кабины.

Определить силу давления тела на пол кабины Р.

Рис.10

Основной закон динамики для тела запишется в виде:

где 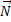- сила реакции опоры.

Рассмотрим два случая:

а) ускорение направлено вверх: m a =N₁–mg,

отсюда N₁=m a+ mg.

По третьему закону Ньютона Р₁=N₁, Р₁= m a+ mg, Р₁=3,84 кН.

б) ускорение направлено вниз: -m a =N₂ - mg,

следовательно N₁=mg–m a, т.е. Р₂=mg- m a, Р₂=2,04 кН.

Пример 4. К нити подвешен груз (рис.11) массой m=1 кг. Найти силу натяжения нити Т, если 1) нить с грузом покоится; 2) двигается вниз с ускорением a= 5 м/с²; 3) двигается вверх с ускорением a= 5 м/с².

Рис.11

На тело действуют две силы: сила тяжести 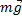и сила натяжения 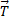. Уравнение движения тела (второй закон Ньютона) в данном случае имеет вид:

Выберем направление оси y вниз и спроецируем на нее векторы сил и ускорения:

1) 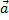=0 ⇒ 0=mg-T ⇒ T=mg=1∙9,8=9,8 Н.

2) 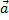направлено вниз ⇒ ma=mg-T ⇒ T=m∙(g-a)=1∙(9,8-5)=4,8 Н.

3) 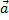направлено вверх ⇒ ma=mg-T ⇒ T=m∙(g+a)=1∙(9,8+5)=14,8 Н.

Пример 5. Груз массой 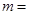50 кг перемещается по горизонтальной плоскости под действием силы F=300 Н, направленной под углом α=30° к горизонтали (рис.12). Коэффициент трения груза о плоскость μ=0,1. Определить ускорение, с которым движется груз.

Рис.12

Уравнение движения тела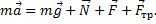

Выберем направления осей х и y и спроецируем на них силы и ускорение:

Поскольку F_тр=μN, а из второго уравнения N=mg-Fsinα, то F_тр=μ(mg-Fsinα). Тогда из первого уравнения ускорение

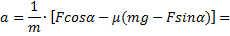
Пример 6. Санки массой m тянут по горизонтальной поверхности с силой F, направленной под углом α к горизонту (рис.12.1). Коэффициент трения между санками и горизонтальной поверхностью равен μ. Определить ускорение санок.

Рис.12.1

Date: 2015-08-15; view: 2486; Нарушение авторских прав