Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Если сумма действующих на тело сил равна нулю, то тело движется равномерно и прямолинейно или находится в покое
Движение, совершаемое точкой при отсутствии сил, называется движением по инерции.
Закон инерции отражает одно из основных свойств материи - пребывать неизменно в движении и устанавливает для материальных тел эквивалентность состояний покоя и движения по инерции. Из него следует, что если F =0, то точка покоится или движется с постоянной по модулю и направлению скоростью (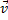
=const); ускорение точки при этом равно нулю: 
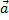= 0); если же движение точки не является равномерным и прямолинейным, то на точку действует сила.
Система отсчета, по отношению к которой выполняется закон инерции, называется инерциальной системой отсчета (иногда ее условно называют неподвижной). По данным опыта для нашей Солнечной системы инерциальной является система отсчета, начало которой находится в центре Солнца, а оси направлены на так называемые неподвижные звезды. При решении большинства технических задач инерциальной, с достаточной для практики точностью, можно считать систему отсчета, жестко связанную с Землей.
Системы отсчета, в которых не выполняется первый закон Ньютона, называются неинерциальными. Неинерциальными будут системы, движущиеся с ускорением, или вращающиеся.
Второй закон (основной закон динамики) гласит: произведение массы точки на ускорение, которое она получает под действием данной силы, равно по модулю этой силе, а направление ускорения совпадает с направлением силы (рис.1).
Рис.1
Математически этот закон выражается векторным равенством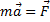 
.
При этом между модулями ускорения и силы имеет место зависимость ma = F.
Второй закон динамики, как и первый, имеет место только по отношению к инерциальной системе отсчета. Из этого закона непосредственно видно, что мерой инертности материальной точки является ее масса, так как две разные точки при действии одной и той же силы получают одинаковые ускорения только тогда, когда будут равны их массы; если же массы будут разные, то точка, масса которой больше (т. е. более инертная), получит меньшее ускорение, и наоборот.
Известно, что вес тела и ускорение его свободного падения пустоте существенно зависят от места земной поверхности. В данной точке земли ускорение свободного падения всех тел одинаково и обозначается буквой g. Экспериментально установлено, что отношение веса Р тела к ускорению его свободного падения g есть постоянная величина, не зависящая от места наблюдения. Это отношение m = P/g также определяет массу тела. Таким образом, различают тяжелую массу m1 = P/g и инертную массу m2 = F/a. В классической механике считается, что m1=m2=m.
Если на точку действует одновременно несколько сил, то они, как известно, будут эквивалентны одной силе, т.е. равнодействующей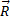 
, равной геометрической сумме этих сил. Уравнение, выражающее основной закон динамики, принимает в этом случае вид
или 
.
Существует и более формулировка второго закона Ньютона: скорость изменения импульса материальной точки равно действующей на нее силе: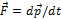 
. Данное выражение называется уравнением движения материальной точки.
В общем случае сила, действующая на тело, изменяется со временем и по величине, и по направлению. Но в течение элементарного промежутка времени dt мы можем считать, что 
=const. Векторная величина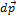 
, равная 
, называется элементарным импульсом (силы).
Второй закон Ньютона в дифференциальной форме:
в проекциях на оси:
Из второго закона также получим размерность силы: 1Н=1 кг∙1 м/с2.
Третий закон (закон равенства действия и противодействия) устанавливает характер механического взаимодействия между материальными телами. Для двух материальных точек он гласит: две материальные точки действуют друг на друга с силами, равными по модулю и направленными вдоль прямой, соединяющей эти точки, в противоположные стороны (рис.2).
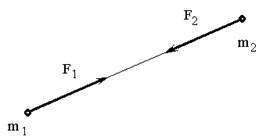
Рис.2
Заметим, что силы взаимодействия между свободными материальными точками (или телами), как приложенные к разным объектам, не образуют уравновешенной системы.
Проведём небольшой эксперимент. Попробуем перемещать тяжёлое тело по некоторой криволинейной траектории. Сразу обнаружим, что тело сопротивляется изменению направления движения, изменению скорости. Возникает сила со стороны тела, противодействующая силе 
, той, которую мы прикладываем к нему.
Эту силу, с которой материальная точка сопротивляется изменению своего движения, будем называть силой инерции этой точки - 
. По третьему закону она равна и противоположна действующей на точку силе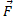 
, 
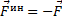. Но на основании второй аксиомы 
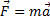. Поэтому 
.
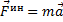Итак, сила инерции материальной точки по величине равна произведению её массы на ускорение
Fин=m a.
И направлена эта сила инерции в сторону противоположную вектору ускорения.
Например, при движении точки по кривой линии ускорение 
. Поэтому сила инерции
.
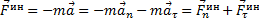То есть её можно находить как сумму двух сил: нормальной силы инерции и касательной силы инерции.
Рис.3
Причём
Необходимо заметить, что сила инерции материальной точки, как сила противодействия, приложена не к точке, а к тому телу, которое изменяет её движение. Это очень важно помнить.
Третий закон динамики, как устанавливающий характер взаимодействия материальных частиц, играет большую роль в динамике системы.
Четвертый закон (закон независимого действия сил). При одновременном действии на материальную точку нескольких сил ускорение точки относительно инерционной системы отсчета от действия каждой отдельной силы не зависит от наличия других, приложенных к точке, сил и полное ускорение равно векторной сумме ускорений от действия отдельных сил.
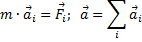
Законы Ньютона в классической механике применимы для описания движения: а) макротел; б) для тел постоянной массы; в) при скоростях, значительно меньших скорости света.
Date: 2015-08-15; view: 3280; Нарушение авторских прав; Помощь в написании работы --> СЮДА... |