А. Булевы операции с объемами понятия

Подобно тому, как в математике проводятся различные операции нзд числами, такие как сложение, вычитание, умножение, деление, воз­ведение в степень и т. д.. в логике также были сформулированы основ­ные принципы проведения операций над объемами понятий, т. е. клас­сами. Поскольку объемы понятий суть множества, над ними можно осу­ществлять те же операции, что и над множествами. Они названы 'Нулевыми в честь английского логика Дж.Буля, который построил осо-■^г)\10 алгебру логики. В числе этих операций пересечение классов, объе­динение классов, дополнение к классу, вычитание классов.

Допустим, даны два понятие хА(х) и хВ(х). таких что объем первого!0{-;ятия есть WxA(x), объем второго понятия есть WxB(x). Тогда опера­ции с объемами понятия будут т меть следующий пил.

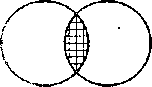
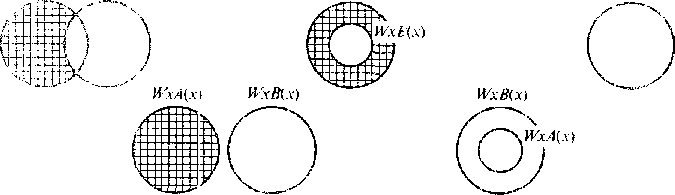
Пересечение двух объемов понятий. Это операция, в результате при­менения которой к объемам понятий WxA(x) и WxB(x) образуется класс И хА{х) г. WxB{x), элементами которого являются те и только те предме­ты, которые одновременно вхоаят как в класс WxA(x), так и в класс IVxBix). Эта операция обозначается знаком "\

Графически класс WxA(x) r\ WxB(x) выделяется при помощи за­штрихованных поверхностей. IV¹ о гут быть следующие случаи пересече­ния объемов понятий.

VVxAix) WxB(x) WxA(x) WxA(x); IVxBix) WxA(x) WxB(x)

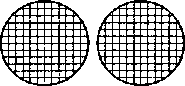
Объединение двух объемов понятий. Это операция, в результате при­менения которой к объемам понятий WxA(x) и WxB{x) образуется класс WxA(x) (\VxB{x), элементами которого являются те и только те предме­ты, которые одновременно входят, по крайней мере, в один из объемов этих понятий. Она обозначается знаком «и».

На схемах класс WxA{x) и {WxB{x) выделен заштрихованными по­верхностями.

WxA{x) IVxBix) iVxA(x) WxA(x); WxB{x) WxA{x) WxBix)

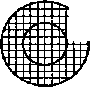WxBix)

Дополнение к объему понятия (взятие дополнения) — это операция, в результате применения которой к объему понятий WxA{x) образуется класс - WxA(x), элементами которого являются те и только те предметы из области значений переменной х, которые одновременно не входят в класс WxA{x). Она обозначается знаком «~».

Графически эта операция представлена в виде, где класс ~WxA(x) обозначен заштрихованной поверхностью.

WxA(x)

IVxB(x)

Университетская серия

Университетская серия

Ь 3. Операции с объемами понятия

■^■i'bHTJ^Hic поил г n'i — что операция, в г)е.?ультате применения кого-! кч,ем; -л пончтий 1УхЛ(х) м Н-'xBU) образуемся класс H'v4(x>\

■(.; ремонтами которого являются it и только гс элементы класса

с,! i'.-ropue одновременно не явдяют:я элементами класса WxB(x). c-o-)тачлечея знаком «\->.

' \:- -лсмач чласс ЛхА(х\\Ц'хВ{х) вы.^ел^н иштрихованными поверх-

it \-i\i Нл8{\) WxAu) IVxAix): WxB(x)

меньшим содержанием (например, понятие -роман, написанный не­мецким писателем» можно обобщить до понятия «роман, написанный европейским писателем»), ин^ми словами, это переход от видового по­нятия к родовому. Пределом обобщения для непустых понятий является универсальное понятие, объем которою совпадает с ролом.

Обратный переход от непустого понятия: данным объемом к более узкому по объему непустому понятию с большим содержанием называ­ют ограничением понятия (наг ример. в результате ограничения понятия «роман, написанный русски\ писателем» можно получить, например. понятие «роман, написанный немецким писателем в XX веке»). Преде­лом ограничения являются единичные понятия.

Операции обобщения и ограничения можно осуществлять посредст­вом модификации содержани 1 понятия, опираясь при этом на закон об­ратного отношения между содержаниями и объемами понятий: чтобы обобщить понятие, необходимо перейти к менее информативному, а чтобы ограничить — к более' информативному понятию.

Особенность применения к объемам понятий булевых операций — ik'hchtiientni, пересечения, разности множеств, взятия дополнения к мно­жеству — сое torn втом, что в результате получается множество, которое чючек'Я объемом нового, сложного понятия, образуемого из содержа-мчи исходных. Так, дополнением к объему понятия является объем отри-ч<числьного понятия. Объединение объемов понятий лае^-] обьем раздели­тельного понятия, пересечение их объемов — объем соединительного по-н■ ) т!!я. ре jy '1 ьтатом теоретико-множественного вычитания второго дйъгма и \ первого будет объем соединительного понятия.

Date: 2015-08-15; view: 725; Нарушение авторских прав