Описание установки. В данной работе измерение радиуса кривизны поверхностей линзы производят на сферометре ИЗС-7 (рис

В данной работе измерение радиуса кривизны поверхностей линзы производят на сферометре ИЗС-7 (рис. 4). Внутри корпуса сферометра расположен измерительный стержень с миллиметровой шкалой, который под действием груза стремится подняться вверх, тем самым обеспечивая контакт сферического наконечника 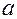с измеряемым изделием. В верхней части корпуса расположено измерительное кольцо 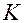(в данной работе из набора взято кольцо № 2 с радиусом шариков 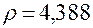мм, радиус кольца – радиус окружности, проходящей через центры шариков, равен 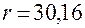мм).

Отсчет по миллиметровой шкале производят с помощью микроскопа 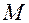со спиральным окулярным микрометром. Освещение шкалы осуществляется лампочкой 3,5 В от сети через трансформатор. Для отвода измерительного стержня служит рычаг – арретир (). Определение радиуса кривизны отдельной выпуклой (в данной работе) сферической поверхности сводится к измерению на сферометре высоты шарового сегмента и вычислению радиуса ее кривизны 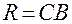по формуле (15):

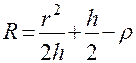. (15)

Вывод формулы (15). Пусть 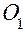и 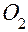– центры шариков кольца (рис.5), 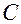– центр сферической поверхности. 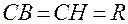(радиус). Из рисунка по известной теореме о перпендикуляре, опущенном из любой точки окружности на диаметр (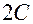), имеем

,

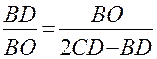но 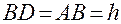, так как точка ниже 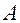, а точка 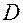– ниже точки 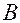на одну и ту же величину 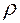. Тогда предыдущее равенство примет вид

,

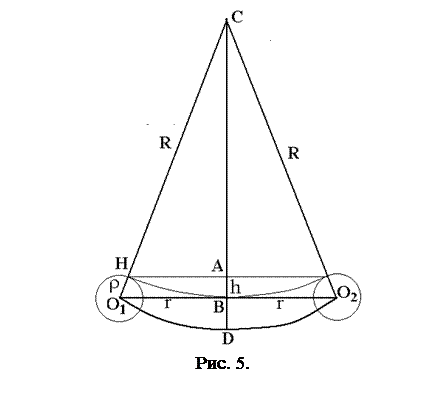
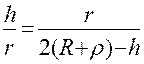откуда после очевидных преобразований получаем формулу (15).

Измерение высоты сферического сегмента () производится следующим образом. На измерительное колльцо осторожно накладывают плоскую стеклянную пластинку, предварительно с помощью рычага арретира () отведя измерительный стержень вниз. Рычаг опускают, и стержень, плавно поднимаясь, приходит в соприкосновение с пластиной. Затем с помощью микроскопа производят отсчет по шкале. Для повышения точности измерений их повторяют 5 раз и вычисляют среднее из полученных отсчетов .

Далее на кольцо помещают линзу сферической поверхностью. Аналогичным образом производят 5 измерений и по ним находят среднее значение 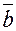. Разность двух средних значений ( 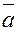- 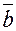) дает величину стрелки .

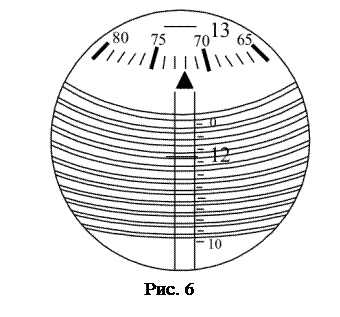
Далее по формуле (15) рассчитывается радиус кривизны линзы 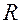. Значение 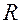в миллиметрах следует округлить до целых.

Отсчеты по шкале спирального окулярного микрометра делаются следующим образом. В поле зрения микроскопа одновременно видны: два-три штриха миллиметровой шкалы, обозначенные цифрами 12, 13,…, неподвижная вертикальная шкала десятых долей миллиметра от 0 до 10, круговая шкала для отсчета сотых и тысячных долей миллиметра и одиннадцать двойных витков спирали (рис. 6). Чтобы произвести отсчет, необходимо предварительно маховичком (рис. 4) подвести двойной виток спирали так, чтобы миллиметровый штрих, находящийся в зоне двойных витков, оказался точно посередине шкалы десятых долей миллиметра. В данном случае число десятых долей миллиметра будет обозначено цифрой 2. Это номер штриха вертикальной шкалы, стоящего перед миллиметровым штрихом 12. Сотые и тысячные доли миллиметра отсчитываются по круговой шкале, указателем отсчета по которой служит стрелка; цена деления круговой шкалы 0,001 мм. Окончательный отсчет будет 12,272 мм.

При измерениях рекомендуется придерживаться следующего порядка:

1. Отвести арретиром измерительный стержень вниз и положить на кольцо плоскую стеклянную пластинку.

2. Произвести по микроскопу 5 отсчетов и найти среднее .

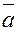3. Заменить пластинку линзой.

4. Произвести отсчеты 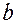для сферической поверхности и найти среднее .

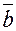5. По формуле (15) рассчитать радиус кривизны линзы 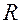, округлить его до миллиметров и занести в таблицу 2.

6. По данным таблиц 1 и 2 рассчитать с помощью формулы (13) показатель преломления стекла линзы.

7. По формуле

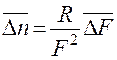(16)

найти ошибку измерения показателя преломления.

Записать ответ в виде .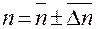

Таблица 1

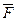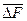№ Измерения	d, мм	f, мм	F, мм	, мм	ΔF, мм	, мм

Таблица 2

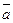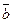№ Измерения	a, мм	, мм	b, мм	, мм	h, мм	r, мм	r, мм	R, мм
						30,16	4,388

Контрольные вопросы

1. В чем состоит основная задача геометрической оптики?

2. Какие закономерности оптических явлений лежат в основе геометрической оптики?

3. Какие лучи называются параксиальными?

4. Как определяется положение оптического центра линзы?

5. Сколько всего оптических осей у линзы? Сколько фокусов?

6. Чем отличается действительное изображение, даваемое линзой, от мнимого? Дать построение. Где получится изображение, если предмет расположить на расстоянии от линзы, равном фокусному?

7. Что называется оптической силой линзы и в каких единицах она измеряется?

8. Где оптическая сила линзы больше – в воздухе или в воде? Во сколько раз?

9. При каких условиях собирающая линза сделается рассеивающей?

10. Как вывести формулу (15)?

11. Почему при работе со сферометром не принимаются поправки на измерения?

12. Вывести формулу (16).

13. Какие правила техники безопасности следует соблюдать при выполнении данной работы?

Date: 2015-08-07; view: 1169; Нарушение авторских прав