Основы теории. Геометрическая оптика представляет собой простой метод построения изображений в оптических системах

Геометрическая оптика представляет собой простой метод построения изображений в оптических системах. Из каждой точки 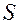светящегося предмета во все стороны расходится пучок лучей. Это может быть либо собственное излучение предмета, либо рассеянные лучи света, освещающего предмет. Часть лучей захватывается оптической системой и сводится в другую точку 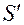, которая становится изображением точки 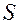. Совокупность изображений всех точек предмета представляет собой изображение этого предмета, полученное с помощью данной оптической системы. При построении изображений в геометрической оптике исходят из следующих соображений:

1. Свет в однородной среде распространяется прямолинейно.

2. Отдельные лучи распространяются независимо друг от друга.

3. При переходе луча из среды с показателем преломления 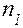в среду с показателем преломления на границе раздела выполняется соотношение между углом падения 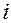и углом преломления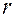

.

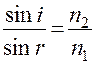4. В данной работе расчет ведется лишь для лучей, распространяющихся под столь малыми углами к оси симметрии оптической системы, что для них можно пользоваться соотношениями 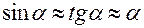. Такие лучи называются параксиальными.

Линзами называются прозрачные для видимого света тела, ограниченные сферическими поверхностями. Линзы являются основными элементами оптических приборов и применяются для получения изображений, преобразования световых пучков и управления ими.

Выведем формулу двояковыпуклой линзы, толщина которой мала по сравнению с радиусами кривизны сферических поверхностей. Такая линза называется тонкой.

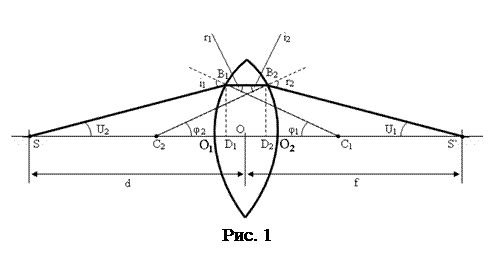
На рис. 1 линза изображена достаточно толстой, чтобы был виден ход лучей внутри нее. Пусть 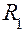и – радиусы кривизны. Обозначим: 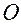– оптический центр линзы; 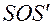- главная оптическая ось; 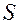– точка изображаемого предмета; 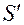- точка изображения; 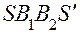- ход луча от точки предмета 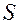до точки изображения 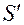. 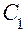– центр кривизны левой (первой) поверхности; 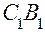– ее радиус кривизны; 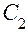– центр кривизны правой (второй) поверхности; 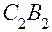– ее радиус кривизны; 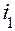и 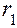– углы падения и преломления луча на левой поверхности линзы; 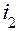и 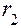– углы падения и преломления луча на правой поверхности линзы; 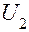и 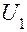– углы наклона предметного и изображающего лучей к главной оптической ос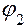и; и 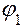– углы наклона радиусов кривизны левой (1) и правой (2) поверхностей.

Прямая, проходящая через оба центра кривизны 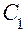и 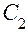, называется главной оптической осью линзы. На главной оптической оси лежит точка, называемая оптическим центром линзы. Наиболее важным свойством оптического центра является то, что любой луч, проходящий через эту точку, не преломляется, т.е. не изменяет своего направления в результате прохождения через линзу. Он только может испытывать параллельное смещение, тем большее, чем толще линза. Для тонких линз это смещение мало, и им обычно пренебрегают. Луч, проходящий через любую другую точку линзы, обязательно преломляется. Оптический центр линзы находят как точку пересечения главной оптической оси и прямой, соединяющей два малых элемента сферических поверхностей, находящихся на концах двух радиусов кривизны, параллельных друг другу (рис. 2).

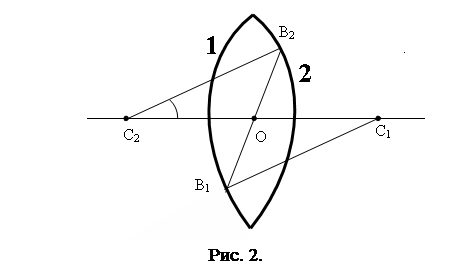
Нахождение оптического центра линзы. 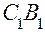и 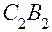– параллельные друг другу радиусы кривизны левой (1) и правой (2) поверхностей линзы. 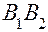– прямая, соединяющая точки пересечения радиусов кривизны с поверхностями линзы.

Вывод формулы линзы по рис.1.

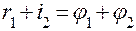(1)

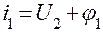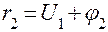, . (2)

Из закона преломления следует

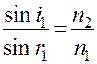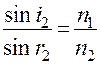и . (3)

Для параксиальных лучей

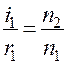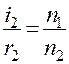и . (4)

Заменяя в (1) углы 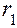и 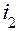равными им по (4), получим

, .

,

,

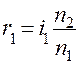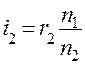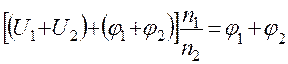отсюда

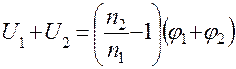, (5)

где – абсолютный показатель преломления стекла, 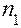- абсолютный показатель преломления среды, где находится линза.

Из рис.1 имеем

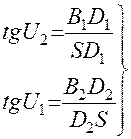; (6)

Для параксиальных лучей тангенсы можно заменить углами и для тонких линз принять, что центры сферических сегментов 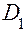и 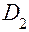сферических поверхностей совмещаются с оптическим центром . Отсюда следует, что можно принять

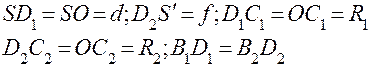. (7)

После замены величин в (5) соответствующими значениями из (6) и (7) и сокращения на 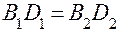получим

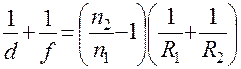. (8)

Показатель преломления воздуха (среда, где находится линза) 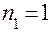; теперь можно записать без индекса, просто 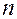. Тогда формула (8) примет вид

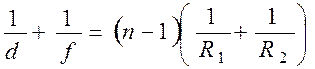. (9)

Полученное выражение представляет собой формулу тонкой двояковыпуклой линзы, находящейся в воздухе. Из школьного курса физики известно, что

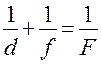, (10)

где 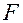– главное фокусное расстояние линзы. Объединяя (9) и (10), получим

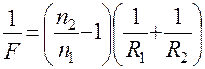. (11)

Величина, обратная фокусному расстоянию, называется оптической силой линзы и обозначается буквой 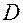: 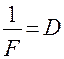Оптическая сила измеряется в диоптриях. 1 диоптрия – это оптическая сила такой линзы, фокусное расстояние которой равно одному метру. Для плосковыпуклой лиинзы 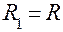, , 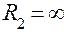и формула (11) примет вид

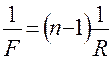, (12)

отсюда

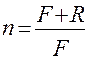. (13)

Следовательно, для определения показателя преломления стекла надо знать радиус кривизны поверхности линзы и главное фокусное расстояние линзы. Последнее можно определить из формулы (10)

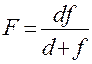, (14)

измерив расстояние от предмета до оптического центра линзы 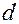и расстояние от оптического центра линзы до изображения 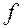. Радиус кривизны линзы измеряют при помощи сферометра.