Критерий Рэлея. Разрешающая способность оптических приборов

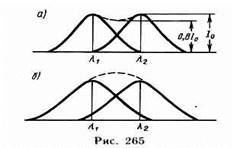
Согласно критерию Рэлея, изображе­ния двух близлежащих одинаковых точеч­ных источников или двух близлежащих спектральных линий с равными интенсивностями и одинаковыми симметричными контурами разрешимы (разделены для восприятия), если центральный максимум дифракционной картины от одного источ­ника (линии) совпадает с первым миниму­мом дифракционной картины от другого (рис. 265, а). При выполнении критерия Рэлея интенсивность «провала» между максимумами составляет 80% интенсив­ности в максимуме, что является достаточ­ным для разрешения линий l₁ и l₂. Если критерий Рэлея нарушен, то наблюдается одна линия (рис. 265, б).

1. Разрешающая способность объекти­ва. Если на объектив падает свет от двух удаленных точечных источников S ₁ и S ₂ (например, звезд) с некоторым угловым расстоянием dj, то вследствие дифракции световых волн на краях диафрагмы, огра­ничивающей объектив, в его фокальной плоскости вместо двух точек наблюдаются максимумы, окруженные чередующимися темными и светлыми кольцами:

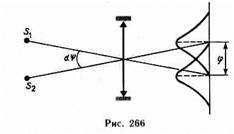уг­ловое расстояние между ними j>=l,22l/D, где Я — длина волны света, D — диаметр объектива.

Разрешающей способностью (разре­шающей силой) объектива называется ве­личина

R=1/dj, где dj — наименьшее угловое расстоя­ние между двумя точками, при котором они еще оптическим прибором разрешаются. Из рисунка следует, что при выполнении критерия Рэлея угловое расстояние между точками dj должно быть равно j, т. е. с учетом dj=j=1,22l/D. Следовательно, разрешающая способ­ность объектива R=1/dj=D/(l,22l), т. е. зависит от диаметра и длины волны света. для увеличения разрешающей способности оп­тических приборов нужно либо увеличить диаметр объектива, либо уменьшить длину волны. Разрешающей способностью спек­трального прибора называют безразмер­ную величину R=l/(dL), где dl — абсолютное значение минималь­ной разности длин волн двух соседних спектральных линий, при которой эти ли­нии регистрируются раздельно.

2. Разрешающая способность дифрак­ционной решетки. Пусть максимум m-го порядка для длины волны l₂ наблюдается под углом j, т.е., d sinj=ml₂. При переходе от максимума к соседнему минимуму разность хода ме­няется на l /N, где N — число щелей решетки. Следовательно, минимум l₁, наблюдаемый под углом j_min, удовлетворяет условию d sinj_min= ml₁+l₁ /N. По критерию Рэлея, j=j_тmin, т.е. ml 2=ml ₁ +l ₁ /N, или l₂/(l₂-l₁)= mN. Так как l₁ и l₂ близки между собой, т.е. l₂-l₁=dl, то, R_{диф.реш}= mN.

Date: 2015-08-06; view: 5747; Нарушение авторских прав