Дифракция света,принцип Гюйгенса-Френеля.Метод Френеля(зоны Ф.,дифрак. На отверстии и круглом диске

Дифракцией называется огибание волна­ми препятствий, встречающихся на их пу­ти, или в более широком смысле — любое отклонение распространения волн вблизи препятствий от законов геометрической оптики. Благодаря дифракции волны могут попадать в область геометрической тени, огибать препятствия, проникать через не­большие отверстия в экранах и т. д.

Дифракция света – это совокупность явлений, наблюдаемых при распространение света сквозь малые отверстия, вблизи границ непрозрачных тел, и т.д. Под дифракцией света обычно понимают отклонения от законов распространения света, описываемых геометрической оптикой. Согласно принципу Гюйгенса — Фре­неля, световая волна, возбуждаемая ка­ким-либо источником S, может быть пред­ставлена как результат суперпозиции ко­герентных вторичных волн, «излучаемых» фиктивными источниками. Такими источ­никами могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в ка­честве этой поверхности выбирают одну из волновых поверхностей, поэтому все фик­тивные источники действуют синфазно. Таким образом, волны, распространяющи­еся от источника, являются результатом интерференции всех когерентных вторич­ных волн. Учет амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду (интенсивность) резуль­тирующей волны в любой точке простран­ства, т. е. определить закономерности рас­пространения света Найдем в произвольной точке М ам­плитуду световой волны, распространяю­щейся в однородной среде из точечного источника S. Согласно принци­пу Гюйгенса — Френеля, заменим дейст­вие источника S действием воображаемых

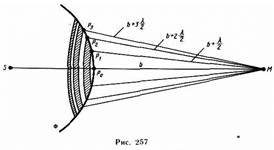
источников, расположенных на вспомога­тельной поверхности Ф, являющейся по­верхностью фронта волны, идущей из S (поверхность сферы с центром S). Фре­нель разбил волновую поверхность Ф на кольцевые зоны такого размера, чтобы расстояния от краев зоны до М отлича­лись на l/2, т. е. Р ₁ М-Р₀М=Р ₂ М -Р ₁ М=Р ₃ М-Р ₂ М=... =l/2. Подобное разбиение фронта волны на зоны можно выполнить, проведя с центром в точке М

сферы радиусами b+l/2, b+2l/2, b +3l/2, ..., b +ml/2. Так как колебания от сосед­них зон проходят до точки М расстояния, отличающиеся на l/2, то в точку М они приходят в противоположной фазе и при наложении эти колебания будут взаимно ослаблять друг друга. Поэтому амплитуда результирующего светового колебания в точке М А=А ₁ -А ₂ +А ₃ -А ₄ +... ±А_т,

где А ₁, А ₂,..., А_m — амплитуды колебаний, возбуждаемых 1-й, 2-й,..., m-й зонами.

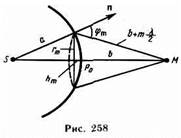
Для оценки амплитуд колебаний най­дем площади зон Френеля. Внешняя гра­ница m-й зоны выделяет на волновой по­верхности сферический сегмент высоты h_m. Обозначив площадь этого сег­мента через s_m, найдем, что площадь m-й зоны Френеля равна Ds_m=s_m-s_m-1 где s_m=1 — площадь сферического сегмен­та, выделяемого внешней границей (т- 1)-й зоны. Из рисунка следует, что

r²_m= а²-(а-h_m)²=(b+ml/2)²-(b+h_m)². После элементарных преобразований, учитывая,

что l<<а и l<<b, получим

h_m=bml/2(a+b). Площадь сферического сегмента s_m=2nph_m=pablm/(a+b), а площадь m-й зоны Френеля

Ds_m=s_m-s_m-1=pabl/(a+b). Выражени не зависит от m; сле­довательно, при не слишком больших m площади зон Френеля одинаковы. Та­ким образом, построение зон Френеля раз­бивает волновую поверхность сферической волны на равные зоны.

Сферическая волна, распространяющаяся из точечного источника 5, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 259). Экран параллелен плоскости отвер­стия и находится от него на расстоянии b. Разобьем открытую часть волновой по­верхности Ф на зоны Френеля. Вид диф­ракционной картины зависит от числа зон Френеля, укладывающихся в отверстии. Амплитуда результирующего колебания, возбуждаемого в точке В всеми зонами, А=А ₁ / 2 ±А_m/ 2,

где знак плюс соответствует нечетным т и минус — четным m Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интен­сивность) в точке В будет больше, чем при

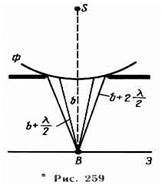свободном распространении волны, если четное, то амплитуда (интенсивность) бу­дет равна нулю. Таким образом, дифрак­ционная картина от круглого отверстия вблизи точки В будет иметь вид чередую­щихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если т нечетное — то светлое кольцо), причем интенсивность максимумов убывает с расстоянием от центра картины. Дифракция на диске. Сферическая волна, распространяющаяся от точечного источника 5, встречает на своем пути диск. Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S с центром диска (рис. 260). В данном случае закрытый диском участок фронта волны надо исклю­чить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает m первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна

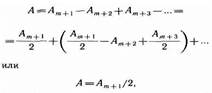
так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответствую­щий половине действия первой открытой зоны Френеля. Центральный максимум ок­ружен концентрическими с ним темными и светлыми кольцами, а интенсивность максимумов убывает с расстоянием от центра картины.

Date: 2015-08-06; view: 470; Нарушение авторских прав