Интерференция света. Методы наблюдения интерференции света. Расчет интерфер. от 2х источников света

Предположим, что две монохроматические световые волны, накладываясь друг на друга, возбуждают в определенной точке пространства колебания одинакового на­правления: x₁ =А ₁ cos (wt+j₁) и x₂= А ₂cos(wt+j₂). Под х понимают на­пряженность электрического Е или маг­нитного Н полей волны; векторы Е и Н ко­леблются во взаимно перпендикулярных плоскостях. Напряженности электрического и магнитного полей под­чиняются принципу суперпозиции. Амплитуда результирую­щего колебания в данной точке А ² =А ²₁ +A ²₂+2 A ₁ A ₂cos(j₂-j₁). Так как волны когерентны, то cos(j₂-j₁) имеет постоянное во времени (но свое для каждой точки пространства) значение, по­этому интенсивность результирующей во­лны (I~А²) I=I₁+I₂+2ÖI₁I₂cos(j₂-j₁).

В точках пространства, где cos(j₂-j₁)>0, интенсивность I>I₁+I₂, где cos(j₂-j₁)<0, интенсивность I<I₁+I₂.

Следовательно, при наложении двух (или нескольких) когерентных световых волн происходит пространственное перераспре­деление светового потока, в результате чего в одних местах возникают максиму­мы, а в других — минимумы интенсивно­сти. Это явление называется интерферен­цией света.

Произведение геометрической длины s пути световой во­лны в данной среде на показатель n пре­ломления этой среды называется оптиче­ской длиной пути L, а D= L ₂- L ₁ — раз­ность оптических длин проходимых во­лнами путей — называется оптической разностью хода.

Если оптическая разность хода равна целому числу волн в вакууме

D=±mlА₀ (m=0, 1, 2,...), (172.2)

то 6= ±2mp и колебания, возбуждаемые в точке М обеими волнами, будут про­исходить в одинаковой фазе. Следователь­но, (172.2) является условием интерферен­ционного максимума.

Если оптическая разность хода

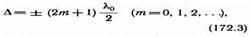то d=±(2m+1)p и колебания, возбуж­даемые в точке М обеими волнами, будут происходить в противофазе. Следователь­но, (172.3) является условием интерферен­ционного минимума.

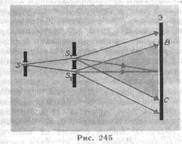
1. Метод Юнга. Источником света слу­жит ярко освещенная щель S (рис.245), от которой световая волна падает на две узкие равноудаленные щели S₁ и S₂, па­раллельные щели S. Таким образом, щели S₁ и S₂ играют роль когерентных источни­ков. Интерференционная картина (об­ласть ВС) наблюдается на экране (Э), расположенном на некотором расстоянии параллельно S₁ и S₂. Как уже указывалось (см. §171), Т. Юнгу принадлежит первое наблюдение явления интерференции.

3. Зеркала Френеля. Свет от источника S (рис. 246) падает расходящимся пучком на два плоских зеркала А ₁ О и A ₂ O, распо­ложенных относительно друг друга под углом, лишь немного отличающимся от 180° (угол j мал). Учитывая правила по­строения изображения в плоских зерка­лах, можно показать, что и источник, и его изображения S ₁ и S₂ (угловое расстояние

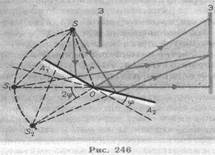
между которыми равно 2j) лежат на од­ной и той же окружности радиуса r с цент­ром в О (точка соприкосновения зеркал). Световые пучки, отразившиеся от обо­их зеркал, можно считать выходящими из

мнимых источников S₁ и S₂, являющихся

мнимыми изображениями S в зеркалах. Мнимые источники S₁ и S₂ взаимно коге­рентны, и исходящие из них световые пуч­ки, встречаясь друг с другом, интерфери­руют в области взаимного перекрывания (на рис. 246 она выполнена зеленым цве­том). Можно показать, что максимальный угол расхождения перекрывающихся пуч­ков не может быть больше 2j. Интерфе­ренционная картина наблюдается на экра­не (Э), защищенном от прямого попадания света заслонкой (3).

3. Бипризма Френеля. Она состоит из двух одинаковых, сложенных основаниями призм с малыми преломляющими углами. Свет от источника S (рис. 247) преломля­ется в обеих призмах, в результате чего за бипризмой распространяются световые лу­чи, как бы исходящие из мнимых источни-

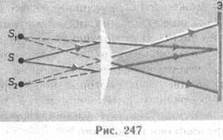ков S ₁ и S ₂, являющихся когерентными. Таким образом, на поверхности экрана (в области, выполненной в цвете) про­исходит наложение когерентных пучков и наблюдается интерференция.

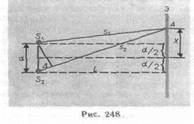
4. Расчет интерференционной картины от двух источников. Расчет интерференци­онной картины для рассмотренных выше методов наблюдения интерференции света можно провести используя две узкие па­раллельные щели, расположенные доста­точно близко друг к другу. Ще­ли S ₁ и S ₂ находятся на расстоянии d друг от друга и являются когерентными (реаль­ными или мнимыми изображениями источ­ника S в какой-то оптической системе) источниками света. Интерференция на­блюдается в произвольной точке А экрана, параллельного обеим щелям и располо­женного от них на расстоянии l, причем l>>d. Начало отсчета выбрано в точке О, симметричной относительно щелей. Интенсивность в любой точке А экра­на, лежащей на расстоянии х от О, опре­деляется оптической разностью хода D=s₂ - s ₁ (см. §172). Из рис. Имеем s ²₂ = l²+(x+d/2) ²; s²₁= l ²+(x-d/2)²,откуда s²₂- s ²₁ =2xd, или D=s₂ -s₁ =2xd/(s₁ +s₂).

Из условия l>>d следует, что s ₁ +s ₂ »2l, поэтому

D= xd/l. Подставив найденное значение D

полу­чим, что максимумы интенсивности будут наблюдаться при

х_max=±т(l/d)l ₀ (m = 0, 1, 2,...),

а минимумы — при x_min=±(m+1/2)(l/d)l₀ (m = 0, 1, 2,...).

Расстояние между двумя соседними максимумами (или минимумами), называ­емое шириной интерференционной полосы, равно

Dx= (l/d)l₀. Dx; не зависит от порядка интерференции (величины m) и является постоянной для данных l, d и l _0.

Date: 2015-08-06; view: 593; Нарушение авторских прав