Домашнее задание

1. Ле­ст­ни­ца дли­ной 4 м при­став­ле­на к глад­кой сте­не под уг­лом 60° к по­лу. На ка­кую мак­си­маль­ную вы­со­ту смо­жет под­нять­ся по ней че­ло­век мас­сой 60 кг, ес­ли мак­си­маль­ное зна­че­ние си­лы тре­ния ме­ж­ду лест­ни­цей и по­лом рав­но 200 Н? Мас­сой ле­ст­ни­цы пре­неб­речь.

(2 м)

2. Под ка­ким ми­ни­маль­ным уг­лом к глад­кой сте­не на­до при­ста­вить ле­ст­ни­цу мас­сой m, что­бы че­ло­век мас­сой M смог под­нять­ся по ней до­вер­ху? Ко­эф­фи­ци­ент тре­ния ме­ж­ду ле­ст­ни­цей и по­лом ра­вен μ.

(tgα = (2 M + m)/2μ(M + m))

3. Палка массой 4,8 кг, прислонённая к стенке под углом 45^о, перестаёт давить на стену, если её подпереть снизу в точке, лежащей посередине между центром тяжести и точкой касания о стену. С какой силой палка давит на пол?

(32 Н)

4. У стены стоит лестница. Коэффициент трения лестницы о землю равен 0,4, о стену 0,3. Какой наименьший угол с горизонтом лестница может образовать, не соскальзывая?

(48^о )

5. Кубик стоит у стены так, что одна из его граней образует угол α с полом. При каком минимальном значении коэффициента трения кубика о пол это возможно, если трением о стену пренебречь.

((cosα ─ sinα)/2sinα)

Се­ми­нар 5. Рав­но­ве­сие сис­те­мы тел

5.1. Однородный стержень массы m одним концом опирается на горизонтальную, другим – на наклонную плоскость (рис. 5.1). Угол между плоскостями a. Какую силу, направленную вдоль наклонной плоскости, надо приложить к одному из концов стержня, чтобы он находился в равновесии? Трением пренебречь.

((mg /2) sina)

5.2. В закреплённой полусфере свободно лежит палочка массы m так, что угол её с горизонтом равен a, а конец выходит за край полусферы (рис.5.2). С какими силами действует палочка на полусферу в точках соприкосновения? Трением пренебречь.

(mg tga, mg cos2a/cosa)

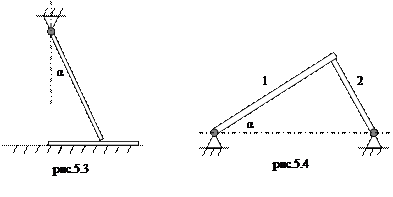
5.4. На гладком горизонтальном столе находится лист бумаги, прижатый однородным стержнем массы m, верхний конец которого шарнирно закреплён (рис. 5.3). Какую минимальную горизонтальную силу необходимо приложить к листу, чтобы вытащить его? Угол между стержнем и листом равен α, коэффициент трения между ними равен μ.

(μ mg /2(1 + μ tgα))

5.3. Лестница-стремянка состоит из двух одинаковых половинок массой m каждая, скреплённых сверху с помощью шарнира. Стремянку раскрывают на угол α и ставят на гладкий пол, а чтобы половинки лестницы не разъезжались, их снизу связывают верёвкой. Найдите силу натяжения верёвки.

(0,5 mg tg(α/2))

5.5. Две тон­кие па­лоч­ки мас­са­ми m ₁ и m ₂ об­ра­зу­ют сис­те­му, изо­бра­жен­ную на рис.5.4. Од­на па­лоч­ка ле­жит сво­им кон­цом на дру­гой палоч­ке, об­ра­зуя пря­мой угол. При ка­ком ми­ни­маль­ном зна­че­нии ко­эф­фи­ци­ен­та тре­ния ме­ж­ду па­лоч­ка­ми сис­те­ма на­хо­дит­ся в рав­но­ве­сии, ес­ли верх­няя па­лоч­ка об­ра­зу­ет с го­ри­зон­том угол α?

((m ₂/ m ₁) tgα)

5.6. На плос­ком ше­ро­хо­ва­том дне ча­ши на­хо­дит­ся шар (рис.5.5). Дно ча­ши на­кло­не­но под не­ко­то­рым уг­лом к го­ри­зон­ту. Шар удер­жи­ва­ет­ся в рав­нове­сии ни­тью, па­рал­лель­ной дну ча­ши. На ка­кой мак­си­маль­ный угол мож­но на­кло­нить дно ча­ши, что­бы шар все еще по­ко­ил­ся, ес­ли ко­эф­фи­ци­ент тре­ния ме­ж­ду ша­ром и дном ча­ши ра­вен μ?

(tgα =2μ)

5.7. На го­ри­зон­таль­ной по­верх­но­сти ле­жат вплот­ную два оди­на­ко­вых брев­на ци­лин­д­ри­че­ской фор­мы (рис.5.6). Свер­ху на них па­рал­лель­но брев­нам кла­дут третье та­кое же брев­но. При ка­ком ми­ни­маль­ном зна­че­нии коэф­фи­ци­ен­та тре­ния ме­ж­ду брев­на­ми они не рас­ка­тят­ся? Счи­тать, что по го­ри­зон­таль­ной по­верх­но­сти брев­на не сколь­зят.

(0,268)

5.8. Два оди­на­ко­вых ша­ра мас­сой m и ра­диу­сом r по­ло­же­ны в вер­ти­каль­ный ци­линдр ра­диу­сом R (R <2 r), от­кры­тый с обо­их кон­цов (рис.5.7). Сис­те­ма на­хо­дит­ся на го­ри­зон­таль­ной по­верх­но­сти. При ка­кой ми­ни­маль­ной мас­се ци­лин­д­ра он не оп­ро­ки­нет­ся?

(2 m (1─ r/R))

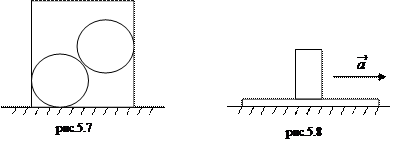
5.9. Тело, имеющее форму прямоугольного параллелепипеда с квадратным основанием со стороной b и высотой h, находится на горизонтальной доске (рис.5.8). Коэффициент трения между телом и доской μ. Доску начинают двигать в горизонтальном направлении с ускорением a. При каком ускорении тело и доска будут двигаться как одно целое?

(a < μg и a < bg / h)

5.10. Ве­ло­си­пе­дист дви­жет­ся по го­ри­зон­таль­ной по­верх­но­сти, по­во­ра­чи­вая по ду­ге ра­диу­сом 100 м с по­сто­ян­ной скор­ос­тью. Най­ди­те мак­си­маль­ную ско­рость ве­ло­си­пе­ди­ста и угол его от­кло­не­ния от вер­ти­ка­ли, что­бы он смог сде­лать та­кой по­во­рот, ес­ли ко­эф­фи­ци­ент тре­ния ме­ж­ду ши­на­ми ве­ло­си­пе­да и по­верх­но­стью ра­вен 0,2.

(14 м/с, 11° )

Date: 2015-08-06; view: 1899; Нарушение авторских прав