Домашнее задание. 1. Ка­туш­ка с на­мо­тан­ной на нее ни­тью ле­жит на го­ри­зон­таль­ных рей­ках и мо­жет дви­гать­ся по ним без сколь­же­ния (рис.18)

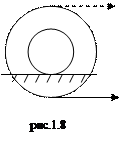1. Ка­туш­ка с на­мо­тан­ной на нее ни­тью ле­жит на го­ри­зон­таль­ных рей­ках и мо­жет дви­гать­ся по ним без сколь­же­ния (рис.18). С ка­кой ско­ро­стью и в ка­ком на­прав­ле­нии бу­дет пе­ре­ме­щать­ся ось ка­туш­ки, ес­ли ко­нец ни­ти тя­нуть го­ри­зон­тально со ско­ро­стью υ? Ра­ди­ус внут­рен­ней час­ти ка­туш­ки r, внеш­ней R. Рас­смот­реть слу­чаи, ко­гда нить на­хо­дит­ся сни­зу и свер­ху внут­рен­ней час­ти ка­туш­ки.

(υr / R – r, υr / R + r)

2. Ре­ши­те за­да­чу 1.7, ес­ли рей­ки дви­жут­ся в про­ти­во­по­лож­ные сто­роны.

(8 рад/с, 2 м/с)

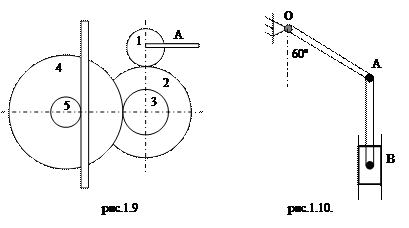
3. В механизме домкрата при вращении рукоятки А начи­на­ют вра­щать­ся шестерни 1, 2, 3, 4 и 5 с радиусами 6 см, 24 см, 8 см, 32 см и 4 см соответ­ственно, которые приводят в движение зубчатую рейку B (рис. 4.9). Найдите ско­рость рей­ки В, если ру­ко­ятку А вра­щают со скоростью 30 об/мин.

(π/4 см/с)

4. Кри­во­шип OA дли­ной 2 м вра­ща­ет­ся во­круг точ­ки O с уг­ло­вой ско­ро­стью 3 рад/с. Най­ди­те уг­ло­вую ско­рость ша­ту­на AB и ли­ней­ную ско­рость пол­зу­на B, ко­гда угол ме­ж­ду кри­во­ши­пом и вертикалью составляет 60^о, а ша­тун занимает вертикальное положение(рис. 4.10). Длина шатуна АВ равна 2 м.

(1,5 рад/с; 3√3 м/с)

Се­ми­нар 2. Рав­но­ве­сие ма­те­ри­аль­ной точ­ки

2.1. Фо­нарь мас­сой 20 кг под­ве­шен над ули­цей на оди­на­ко­вых тро­сах, угол ме­ж­ду ко­то­ры­ми ра­вен 120°. Най­ди­те си­лы на­тя­же­ния тро­сов.

(200 Н)

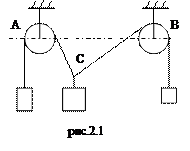
2.2. К кон­цам ни­ти, пе­ре­ки­ну­той че­рез не­под­виж­ные бло­ки A и B, под­ве­ше­ны гру­зы (рис.2.1). Ко­гда в точ­ке C ни­ти под­ве­си­ли тре­тий груз мас­сой 150 г, угол ABC стал ра­вен 30°, а угол BAC ра­вен уг­лу BCA. Най­ди­те мас­сы гру­зов.

(135 г, 41 г)

2.3. Ве­рев­ка при­вя­за­на к крюч­ку A и пе­ре­ки­ну­та че­рез не­под­виж­ный блок C (рис.2.2). К ве­рев­ке в точ­ке D при­кре­п­лен груз мас­сой 20 кг, при­чем точ­ка D не мо­жет пе­ре­ме­щать­ся по ве­рев­ке. Груз ка­кой мас­сы сле­ду­ет при­кре­пить к кон­цу ве­рев­ки в точке B, что­бы си­ла на­тя­же­ния ве­рев­ки на уча­ст­ке AD бы­ла вдвое боль­ше си­лы на­тя­же­ния в ос­таль­ной ее час­ти, а угол ADC был пря­мой?

(8,9 кг)

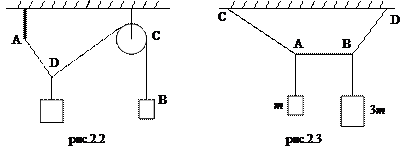
2.4. На тро­се, сред­няя часть ко­то­ро­го го­ри­зон­таль­на, под­ве­ше­ны два гру­за мас­са­ми m =1 кг и 3 m (рис.2.3). Най­ди­те си­лы на­тя­же­ния в ка­ж­дой час­ти тро­са, ес­ли уча­сток тро­са AC со­став­ля­ет с по­тол­ком угол 30°.

(20 Н, 17 Н, 34 Н)

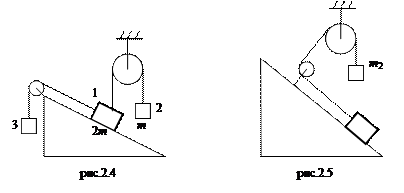
2.5. Сис­те­ма, изо­бра­жен­ная на рис.2.4, на­хо­дит­ся в рав­но­ве­сии. Най­ди­те мас­су гру­за 3 и си­лу дав­ле­ния, про­из­во­ди­мо­го гру­зом 1 на гладкую на­клон­ную плос­кость, со­став­ляю­щей с го­ри­зон­том угол α.

(m sinα, mg cosα)

2.6. Тело массой 1 кг находится на наклонной плоскости с углом 45^о к горизонту (рис.2.5). Груз какой массы m ₂ надо подвесить через систему блоков к первому телу, чтобы тела находились в покое? Коэффициент трения между телом и наклонной плоскостью равен 0,2.

(0,56 кг < m ₂ < 0,84 кг)

2.7. На крон­штей­не ви­сит груз мас­сой 100 кг (рис.2.6). Най­ди­те силы ре­ак­ции в стерж­нях AC и BC, ес­ли угол ACB ра­вен 60°. Стерж­ни крон­штей­на не­ве­со­мы.

(578 Н, 1156 Н)

2.8. К глад­кой вер­ти­каль­ной сте­не на тро­се дли­ной 4 м под­ве­шен шар мас­сой 300 кг и ра­диу­сом 2,5 м (рис.2.7). Най­ди­те си­лу дав­ле­ния шара на сте­ну и си­лу на­тя­же­ния тро­са.

(1250 Н, 3250 Н)

2.9. Шар мас­сой √3 кг на­хо­дит­ся внут­ри дву­гран­но­го уг­ла, об­ра­зо­ван­но­го вер­ти­каль­ной сте­ной и на­клон­ной плос­ко­стью, со­став­ляю­щей с го­ри­зон­том угол 30° (рис.2.8). Най­ди­те си­лы дав­ле­ния ша­ра на плос­ко­сти.

(10 Н, 20 Н)

2.10. В системе (рис.2.9), состоящей из куба массой m ₁ и призмы массой m ₂, найдите минимальное значение коэффициента трения между призмой и горизонтальной поверхностью, при котором система покоится. Трением между кубом и вертикальной стенкой, кубом и призмой пренебречь.

(m ₁/√3(m ₁ + m ₂))

2.11. Сис­те­ма, со­стоя­щая из гладкого ци­лин­д­ра мас­сой 2√3 кг и приз­мы мас­сой 1 кг, на­хо­дит­ся ме­ж­ду дву­мя на­клон­ны­ми плос­ко­стя­ми AB и BC, состав­ляю­щи­ми с го­ри­зон­том уг­лы 30° и 45° со­от­вет­ст­вен­но (рис.2.10). При ка­ком ми­ни­маль­ном зна­че­нии ко­эф­фи­ци­ен­та тре­ния ме­ж­ду приз­мой и на­клон­ной плос­ко­стью BC сис­те­ма бу­дет на­хо­дит­ся в рав­но­ве­сии?

(1/3)

Date: 2015-08-06; view: 1378; Нарушение авторских прав