Тепловое самовоздействие

Среди рассмотренных нелинейных оптических эффектов особое место занимает тепловое самовоздействие. Оно является наиболее низкопороговым и, вследствие этого, легко наблюдается при распространении в среде даже слабого лазерного излучения с мощностью не превышающей 10 ^{– 3} Вт.

Основные физические процессы, лежащие в основе данного эффекта, следующие:

1. Распространение монохроматического излучения в поглощающей среде сопровождается достаточно сильной диссипацией электромагнитной энергии (переходом ее в тепловую энергию движения частиц среды).

2. Диссипация энергии электромагнитного поля сопровождается сильным нагреванием среды, приводящим к повышению температуры в областях сильного поглощения.

3. Локальное повышение температуры приводит к изменению плотности среды. Изменение плотности среды с температурой при постоянном давлении можно представить так: 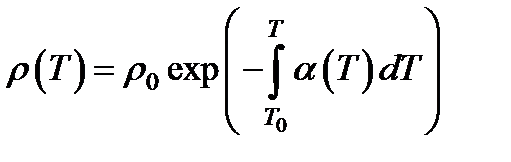, где r ₀ = r (T), 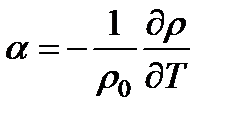- коэффициент теплового расширения, зависящий в общем случае от температуры. Если a = const, то при небольших изменениях температуры выражение можно упростить: ,

4. Локальное изменение плотности среды приводит к локальному изменению показателя преломления. Показатель преломления вещества определяется уравнением Клаузиуса-Мосотти: ,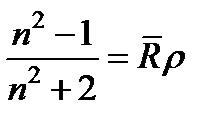

где 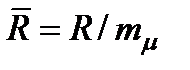- массовый показатель преломления (R - поляризуемость одного моля, m_m - молярная масса), не зависящий от температуры, r - плотность вещества. Тогда 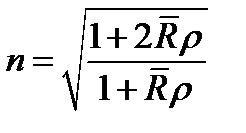. Подставив в полученное выражение значение плотности из, после преобразования получаем: n = n (T ₀) - c ₁ dT. Если учесть, что изменение температуры d T пропорционально поглощаемой, а следовательно, и падающей мощности или интенсивности, то закон изменения показателя преломления принимает следующий вид:, где c ₁, n ₂ - постоянные величины, зависящие от свойств среды. Таким образом тепловое самовоздействие излучения приводит к известному уже нелинейному закону изменения показателя преломления с отрицательной нелинейной поправкой.

Локальное изменение показателя преломления, возникающие на пути распространения светового излучения, приводит к отклонению направления его распространения от прямолинейного. Обычно в эксперименте используют пучки света конечного поперечного сечения, по которому плотность потока энергии распределена неравномерно, следовательно, и показатель преломления изменяется по сечению пучка. Для определенности положим сечение пучка круглым с эффективным радиусом a ₀, а распределение средней плотности потока энергии (интенсивности) - подчиняющимся закону Гаусса: ,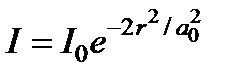

где I ₀ - интенсивность в центре пучка (r = 0). Как известно, в зависимости от характера нелинейности, знак нелинейной поправки к показателю преломления может быть как положительным, так и отрицательным.

Если нелинейная поправка положительна, то скорость распространения периферийных участков волны (v = c / n) больше, чем центральных, в результате первоначально плоский фронт выгибается в сторону распространения пучка и фокусируется на оси (рис. 8.10) - возникает явление самофокусировки, о котором уже шла речь

Рис. 8.10 Рис. 8.11

Если нелинейная поправка отрицательна, происходит расширение пучка, его дефокусировка, поскольку скорость распространения центральных участков пучка больше скорости периферийных (рис. 8.11). В этом случае выражение 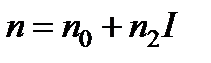с учетом принимает вид: ,

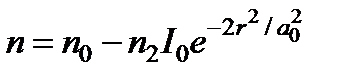Из анализа данного выражения следует, что на оси пучка (r = 0) показатель преломления минимален и равен n (0) = n ₀ + n ₂ I ₀, причем следует напомнить, что n ₂ I ₀ << n ₀, Графическое изображение показателя преломления в сечении пучка лазерного излучения с гауссовым распределением интенсивности имеет вид, представленный на рис. 8.12.

Рис. 8.12 Рис. 8.13

Сделаем оценку угла нелинейной расходимости q_l при прохождении им слоя вещества толщиной l (рис. 8.13). Рассмотрим луч света, падающий под небольшим углом a₀ на слой вещества толщиной l. Вследствие неоднородности показателя преломления вдоль радиуса падающего пучка, выходящий луч окажется отклоненным на угол q_l. Распределение показателя преломления как следует из, аксиально симметрично относительно оси Oz.

Закон преломления рассматриваемого луча на первой и второй границах слоя запишется в виде:

, .

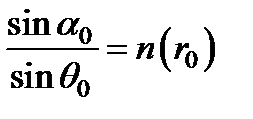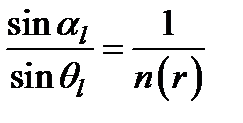Закон преломления в произвольной точке траектории луча (например, в точке P) можно представить так: 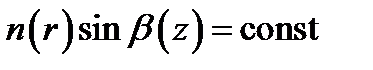. Тогда для интересующих нас углов q закон принимает вид: ,

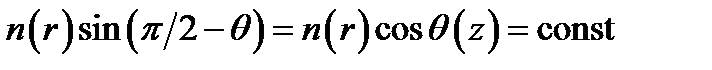Применим полученное выражение к первой граничной и к какой-либо параллельной ей произвольной поверхностям: ,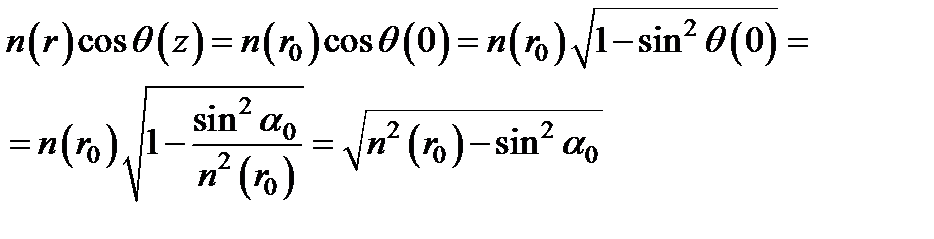

Отсюда выразим: ,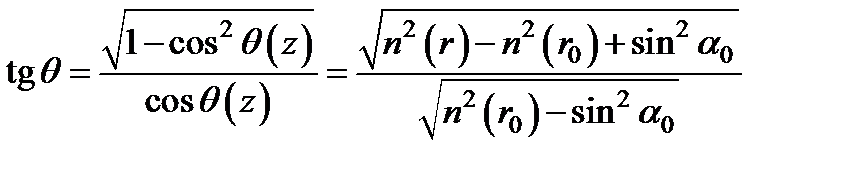

Вследствие относительно малого изменения показателя преломления вдоль толщины слоя, можно представить как 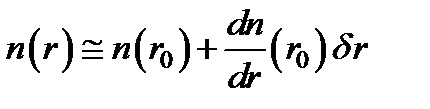, откуда: 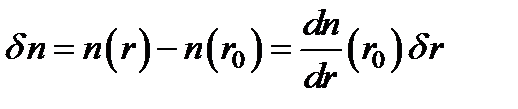.Тогда:

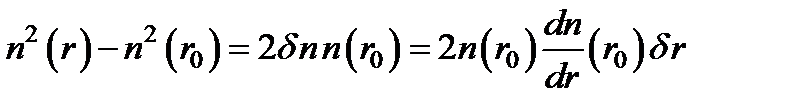. Полученное выражение подставим в:

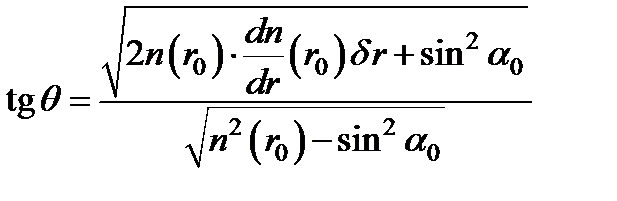. Угол падения луча на первую грань a₀ можно положить равным нулю (a ₀ = 0), тогда 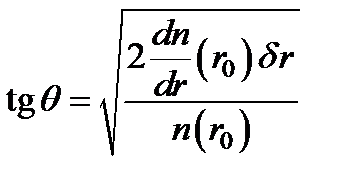. С другой стороны .

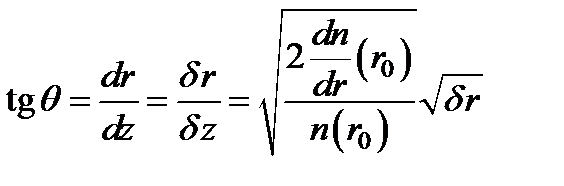Возводя это выражение в квадрат, определим 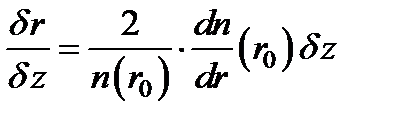. При этом искомое значение угла отклонения луча принимает вид: .

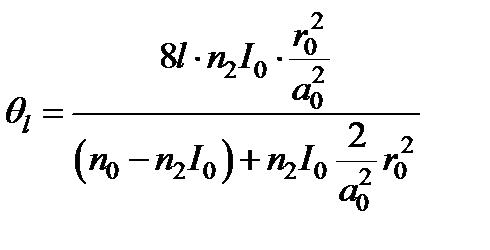Подставим в значение показателя преломления из, предварительно разложив его в ряд и ограничившись двумя первыми членами ,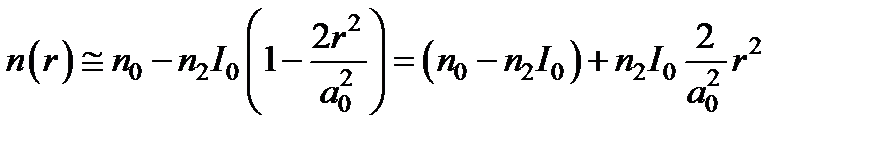

так что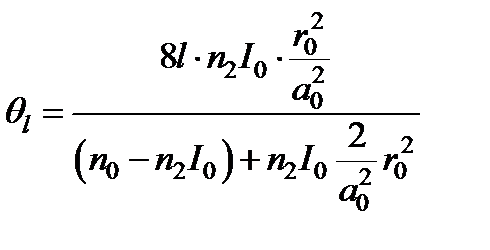

Из анализа выражения видно, что угол отклонения луча зависит от координат его точки падения (r ₀) на поверхность слоя. Луч, падающий вдоль оси Oz, не испытывает углового смещения, тогда как луч с координатой r ₀ = a ₀ испытывает максимальное угловое смещение

Качественный анализ полученного выражения позволяет нам сделать вывод о том, что увеличить угол расходимости пучка можно двумя способами: 1) увеличением интенсивности падающего пучка I ₀; 2) уменьшением a ₀, т.е. первоначальной фокусировкой падающего пучка.

· Основные свойства электромагнитных волн

· Электромагнитная природа света(1) Свойства электромагнитных волн(1)

· Волновое уравнение(1) Плоская волна(2) Плоская гармоническая волна(2-3) Сферическая волна(3) Сферическая гармоническая волна(4) Свойства плоской гармонической электромагнитной волны(4-5) Плотность потока энергии(5)

· Принцип суперпозиции(5-6) Биения(6-7) Стоячие волны(7-9) Опыты Винера(9)

· Поляризация электромагнитных волн(10)

· Эллиптическая поляризация(10-11) Правая и левая эллиптические поляризации(11-12) Линейная и круговая поляризации(12-13) Параметры Стокса(13-15) Сфера Пуанкаре(13-15)

· Фотометрия(15-22)

· Немонохроматическое излучение

· Спектральные разложения в оптике(23)

· Метод спектральных разложений(23) Периодические функции(23-24) Ряд Фурье(23-24) Дискретный спектр(23-24) Спектральные амплитуды и фазы(24) Непериодические функции(25) Интеграл Фурье(25) Сплошной спектр(25) Спектральная амплитуда и спектральная фаза(26) Комплексная запись(27) Примеры(27) Связь между длительностью импульса и шириной спектра(28) Полная и неполная спектральная информация(28-29) Спектральная плотность(28-29) Равенство Парсеваля(29)

· Классическая модель излучателя электромагнитных волн(29-30)

· Излучение диполя(30-31) Гармонические колебания диполя(31-32) Радиационное затухание(32-33) Естественная ширина линии излучения(34-35)

· Уширение спектральных линий(35-36)

· Доплеровское уширение(36-37) Форма составной линии излучения(37)

· Волновые пакеты(38)

· Волновой пакет, образованный двумя волнами(38) Групповая скорость(38-39) Суперпозиция колебаний с эквидистантными частотами(39-40)

· Модулированные волны(40)

· Модуляция амплитуды(40-41) Модуляция частоты и фазы(41-42) Спектр колебания с гармонической модуляцией частоты(42)

· Интерференция света

· Интерференция света(43)

· Интерференция монохроматического света(43-44) Общая интерференционная схема(44-45) Ширина интерференционной полосы(45) Распределение интенсивности(45)

· Когерентность(46-47)

· Длина когерентности(46-47) Ширина когерентности(47-48)

· Интерференционные схемы(48)

· Бипризма Френеля(48-49) Бизеркала Френеля(49-50) Билинза Бийе(50-51)

· Интерференция немонохроматического света(51-53)

· Понятие о временной когерентности(51-53)

· Интерференция от протяженного источника(54-55)

· Понятие о пространственной когерентности(54-55) Пространственная когерентность(56) Угол и ширина когерентности(56)

· Интерференция света в тонких пленках(57-59)

· Итерференционная картина, получаемая с помощью плоскопараллельной пластинки(57-59) Итерференционная картина, получаемая с помощью пластинки переменной толщины(60-62)

· Многолучевая интерференция(62-66)

· Интерферометр Фабри – Перо(66-69)

· Дифракция света

· Дифракция света(69-70) Принцип Гюйгенса – Френеля(69)

· Дифракционный интеграл Френеля(70-72)

· Дифракция Френеля на простейших препятствиях(72-44) Графический способ решения дифракционных задач(73-74) Спираль Френеля(72-73)

· Спираль Френеля(72-73) Дифракция на круглом отверстии(73-74) Дифракция на диске(75) Пятно Пуассона(75) Зонная пластинка(75-76)

· Дифракция Френеля на полуплоскости и щели(76-77) Спираль Корню(77-78)

· Дифракция от прямолинейного края полуплоскости(76-77) Спираль Корню(77-78) Дифракция от щели(78-79)

· Свободное распространение плоской волны и нормировка интеграла Гюйгенса – Френеля(79-82)

· Дифракция Фраунгофера(82-83)

· Дифракция Фраунгофера на щели(83-85) Дифракция на двух щелях(85-87) Дифракционная решетка(87-89)

· Дифракция Фраунгофера на отверстиях произвольной формы(90-92)

· Теория дифракции Кирхгофа(93)

· Уравнение Гельмгольца(93) Интегральная теорема Кирхгофа –Гельмгольца(93-95)

· Основные понятия Фурье-оптики(95-96)

· Спектральное описание пространственной структуры поля(96-97) Инварианты распространения светового пучка(97) Приближение Френеля(97-98) Дифракционная расходимость излучения(98) Линза, как элемент, выполняющий пространственное преобразование Фурье(98-99) Коэффициент передачи тонкой линзы(99-100) Распределение света в фокальной плоскости линзы(100-101) Формирование оптического изображения(101-102) Опыты Аббе – Портера(102-103) Метод темного поля(103) Метод фазового контраста(103-104) Разрешающая способность микроскопа и телескопа(104-105) Электронный микроскоп(105) Телескоп(105-106)

· Физические принципы голографии(106)

· Запись светового поля(107) Восстановление поля(107) Классификация голограмм(107-110) Практические приложения голографии(110-111) Свойства голограмм(111)

· Распространение света в изотропных средах

· Распространение световых волн в однородных изотропных средах(112)

· Классическая электронная теория дисперсии(113-117)

· Анализ дисперсионной формулы(117-120)

· Дисперсия в металлах(120-122) Поглощение света(123-124)

· Отражение и преломление световых волн на границе раздела двух диэлектриков(124-125)

· Законы отражения и преломления света(124-125)

· Формулы Френеля(126-127)

· Анализ формул Френеля(128)

· Фазовые соотношения(128) Отражательная и пропускательная способности(128-132) Поляризация при отражении и преломлении(128-132)

· Рассеяние света(132-135)

· Рэлеевское рассеяние света(136-137) Поляризация рассеянного света(137) Молекулярное рассеяние(138-139)

· Распространение света в анизотропных средах

· Анизотропные среды(140-141) Двойное лучепреломление(140-141)

· Плоские монохроматические волны в анизотропной среде(141-145) Одноосные кристаллы(141-145)

· Преломление на границе анизотропной среды(145-148) Построения Гюйгенса(145-148)

· Кристаллические фазовые пластинки(149-151)

· Прохождение света через поляризатор(151-152) Закон Малюса(152)

· Интерференция поляризованных волн при прохождении через кристаллы(153-154)

· Вращение плоскости поляризации(155-156)

· Естественное вращение плоскости поляризации(155-156) Феноменологическая теория вращения плоскости поляризации(156-158)

· Магнитное вращение плоскости поляризации(158-160)

· Применение явления вращения плоскости поляризации(160)

· Искусственная анизотропия(161)

· Анизотропия при деформации(161) Анизотропия, создаваемая в веществе электрическим полем(161-162) Анизотропия, создаваемая в веществе магнитным полем (явление Коттона-Мутона)(162) Эффект Поккельса(162-163)

· Геометрическая оптика

· Геометрическая оптика как предельный случай волновой оптики(163-168)

· Преломление на сферической поверхности(168-169)

· Изображение малых предметов(169-170) Увеличение(169-170)

· Общая формула линзы(170-172)

· Центрированная оптическая система и ее кардинальные элементы(172-174)

· Аберрации оптических систем(175-176) Источники аберраций(175-176)

· Элементы квантовой оптики

· Исследование равновесного теплового излучения(177-180)

· Формула Рэлея – Джинса(180) Формула Вина(180) Формула Планка(181) Закон Стефана – Больцмана(182) Закон смещения Вина(182)

· Усиление и генерация света(183)

· Спонтанные и вынужденные переходы(183) Коэффициенты Эйнштейна(183-184) Оптические усилители и генераторы(184-185) Условия усиления(185) Воздействие светового потока на заселенность уровней(185-186) Условия насыщения(186) Создание инверсной заселенности(186) Принципиальная схема лазера(187-189) Порог генерации(189) Условия стационарной генерации(190) Добротность(190) Непрерывные и импульсные лазеры(190) Метод модулированной добротности(191)

· Нелинейные явления в оптике(191)

· Взаимодействие света со средой(191-194) Поляризованность среды(191-194) Основные нелинейные эффекты(194-195)

· Первое приближение(195-198) Оптическое детектирование(195-198) Генерация второй гармоники(195-198)

· Второе приближение(198-200) Эффекты самовоздействия(198-200)

· Параметрическая генерация света(200-201) Тепловое самовоздействие(201-203)

Date: 2015-08-06; view: 527; Нарушение авторских прав