
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Второе приближение. Эффекты самовоздействия
|
|
Для нахождения второго приближения надо использовать вектор 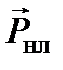 в первом приближении, т.е.
в первом приближении, т.е. 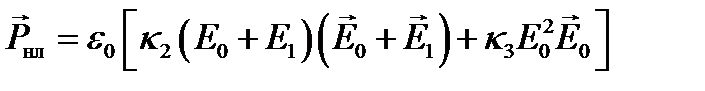 Если ограничиться только изотропными средами или кристаллами, обладающими центом симметрии, то как было сказано, k 2 = 0, и следовательно, в нужном приближении
Если ограничиться только изотропными средами или кристаллами, обладающими центом симметрии, то как было сказано, k 2 = 0, и следовательно, в нужном приближении 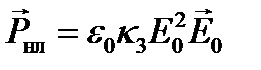 . Взяв в качестве нулевого приближения плоскую волну
. Взяв в качестве нулевого приближения плоскую волну 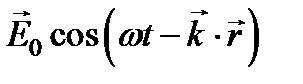 получим:
получим: 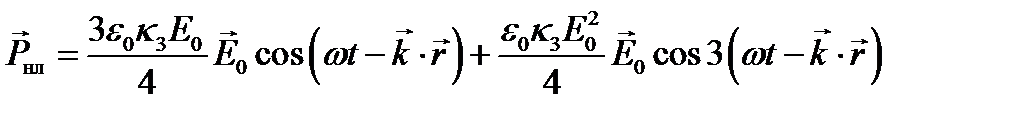 .
.
Слагаемое с тройной частотой w 3 = 3 w приводит, очевидно, к генерации третьей гармоники. Исходное излучение частотой w создает в нелинейной среде поляризованность, осциллирующую на утроенной частоте 3 w Элементарные вторичные волны третьей гармоники, испускаемые разными элементами среды, будут иметь всюду одинаковые фазовые соотношения с возбуждающей их волной поляризованности при совпадении показателей преломления на частотах w и 3 w. Дисперсия среды на интервале (w, 3 w) еще больше, чем в случае второй гармоники. Это ограничивает выбор кристаллов, в которых возможно выполнение условия пространственного синхронизма (n (3 w) = n (w)), так как двулучепреломление должно быть настолько большим, чтобы поверхности n 0(w) = ne (3 w) еще пересекались. Кроме того кубичная восприимчивость имеет малое значение, что вынуждает применять очень интенсивное исходное излучение. Мощное исходное излучение может привести к разрушению кристалла, но, несмотря на это, генерация третьей гармоники наблюдалась еще в 1962 г. группой американских ученых на кристалле исландского шпата при освещении его светом рубинового лазера.
Посмотрим теперь, какие явления связаны с первым слагаемым в выражении. Множитель 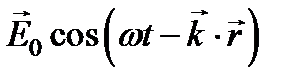 есть исходная падающая волна. В рассматриваемом приближении этот множитель можно заменить
есть исходная падающая волна. В рассматриваемом приближении этот множитель можно заменить 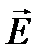 . Учитывая, что
. Учитывая, что 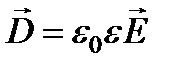 , формулу
, формулу 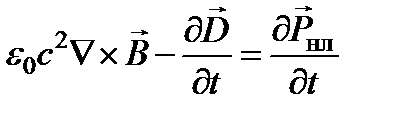 (2-е уравнение Максвелла с учетом нелинейной части поляризованности) после этого можно записать так:
(2-е уравнение Максвелла с учетом нелинейной части поляризованности) после этого можно записать так:
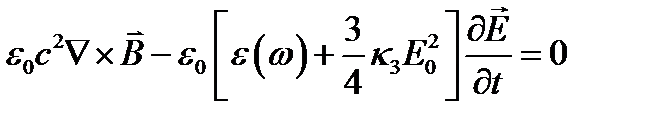 .
.
Отсюда видно, что влияние рассматриваемого слагаемого эквивалентно изменений диэлектрической проницаемости или показателя преломления среды. Учитывая малость поправки к e (w), для показателя преломления в поле интенсивной световой волны можно написать
 ,
, 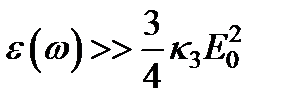 ,
,
где 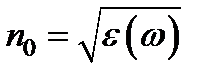 - значение показателя преломления среды в линейной оптике, а n 2 = 3 k 3/8 n 0 - некоторый коэффициент, зависящий от свойств среды. Этот коэффициент может быть и отрицательным, и положительным. Он особенно велик у нитробензола и имеет для него положительный знак.
- значение показателя преломления среды в линейной оптике, а n 2 = 3 k 3/8 n 0 - некоторый коэффициент, зависящий от свойств среды. Этот коэффициент может быть и отрицательным, и положительным. Он особенно велик у нитробензола и имеет для него положительный знак.
Согласно, чем больше интенсивность падающей волны, тем большее изменение показателя преломления она вызывает. За счет появления нелинейной добавки к диэлектрической проницаемости (показателю преломления) световая волна изменяет собственную скорость и коэффициент поглощения в среде, т.е. волна, изменяя характеристики среды, тем самым изменяет условия для своего распространения. Это приводит к эффектам самофокусировки, самодифракции, нелинейному расширению светового пучка и т.д. Такие оптические эффекты принято называть самовоздействием световой волны.

Р и с. 8.9
Чтобы представить сущность явления самофокусировки, предположим, что в однородную среду с показателем n 0 вступает плоскопараллельный пучок лучей кругового сечения с диаметром D (рис. 8.9). Допустим, что амплитуда пучка постоянна по всему сечению. Показатель преломления в пространстве, занятом пучком, станет равным 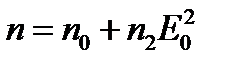 , причем предположим, что n 2 > 0. Из-за дифракции пучок должен расширяться, так что все направления лучей сосредоточатся в пределах конуса с углом при вершине 2 q диф, где q диф = 1,22 l / Dn 0, l - длина волны в вакууме. Так как показатель преломления в пространстве, занятом пучком, больше, чем в окружающей среде, то на границе этих сред возможно полное внутреннее отражение, предельный угол скольжения для полного отражения от боковой стенки цилиндра определяется соотношением cos q 0 = n 0/(n 0 + n 2 E 02).
, причем предположим, что n 2 > 0. Из-за дифракции пучок должен расширяться, так что все направления лучей сосредоточатся в пределах конуса с углом при вершине 2 q диф, где q диф = 1,22 l / Dn 0, l - длина волны в вакууме. Так как показатель преломления в пространстве, занятом пучком, больше, чем в окружающей среде, то на границе этих сред возможно полное внутреннее отражение, предельный угол скольжения для полного отражения от боковой стенки цилиндра определяется соотношением cos q 0 = n 0/(n 0 + n 2 E 02).
Ввиду малости нелинейной поправки к показателю преломления, этот угол будет мал, так что 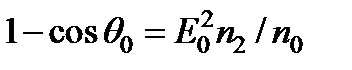 . При разложении функции cos q 0 в степенной ряд получим
. При разложении функции cos q 0 в степенной ряд получим 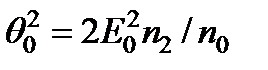 . Если q диф < q 0, то часть дифрагированных лучей будет выходить из цилиндра - пучок будет 'расширяться, при обратном соотношении q диф < q 0 все дифрагированные лучи будут испытывать полное отражение от боковой поверхности цилиндра. Так как в реальных световых пучках интенсивность света и показатель преломления возрастают к оси пучка, то из-за искривления лучей пучок начинает сжиматься и может стянуться в тонкий шнур. Это и есть самофокусировка. В промежуточном случае когда
. Если q диф < q 0, то часть дифрагированных лучей будет выходить из цилиндра - пучок будет 'расширяться, при обратном соотношении q диф < q 0 все дифрагированные лучи будут испытывать полное отражение от боковой поверхности цилиндра. Так как в реальных световых пучках интенсивность света и показатель преломления возрастают к оси пучка, то из-за искривления лучей пучок начинает сжиматься и может стянуться в тонкий шнур. Это и есть самофокусировка. В промежуточном случае когда 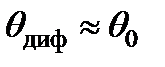 , пучок будет проходить через нелинейную среду практически без изменения поперечных размеров. Он создаст для себя как бы волновод, в котором и распространяется без рассеяния в стороны. Такой режим распространения называется самоканализацией светового пучка. Так как условие самоканализации имеет вид
, пучок будет проходить через нелинейную среду практически без изменения поперечных размеров. Он создаст для себя как бы волновод, в котором и распространяется без рассеяния в стороны. Такой режим распространения называется самоканализацией светового пучка. Так как условие самоканализации имеет вид 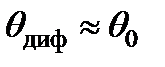 , то подставив сюда значения углов
, то подставив сюда значения углов 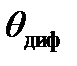 и
и 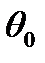 и выражение амплитуды через мощность пучка
и выражение амплитуды через мощность пучка 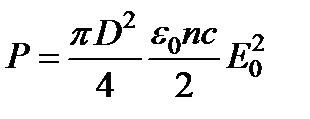 , получим так называемую пороговую мощность пучка
, получим так называемую пороговую мощность пучка 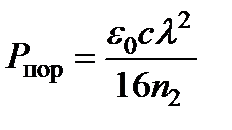 , выше которой и начинается сжатие пучка. Заметим, что для наблюдения любого нелинейного эффекта необходимы световые пучки с определенными пороговыми мощностями.
, выше которой и начинается сжатие пучка. Заметим, что для наблюдения любого нелинейного эффекта необходимы световые пучки с определенными пороговыми мощностями.
Помимо рассмотренной, как уже отмечалось, есть и другие причины изменения показателя преломления. Это и электрострикция, и высокочастотный эффект Керра, и нагревание среды, происходящее при поглощении световой волны. Во всех этих случаях изменение показателя преломления пропорционально квадрату амплитуды волны и может быть определено формулой 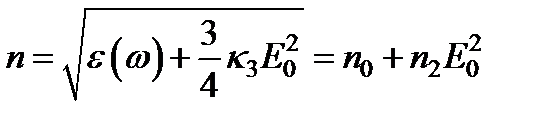 ;
; 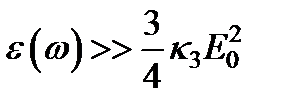 .
.
Date: 2015-08-06; view: 469; Нарушение авторских прав