Взаимодействие света со средой. Поляризованность среды

Оптические свойства среды в линейной оптике описываются такими не зависящими от интенсивности характеристиками, как коэффициент преломления n и коэффициент поглощения χ. Объяснение преломления и поглощения света и схема расчета величин n и χ хорошо известны. Обратимся сначала к классической лоренцевской модели гармонического осциллятора - одиночного атома, содержащего ядро и единственный электрон. Если к этому атому приложить электрическое поле, то расстояние между электроном и ядром изменится, у атома появится электрический дипольный момент - он поляризуется. Если электрическое поле изменяется, то и поляризация в модели Лоренца изменяется аналогичным образом; частота изменения равна частоте изменения приложенного поля. Другими словами, электрон в переменном электрическом поле колеблется около своего положения равновесия, образуя колеблющийся диполь. Этот диполь излучает электромагнитную волну, частота которой равна частоте колебаний диполя и следовательно частоте приложенного поля. Фаза волны также, как и фаза колебаний диполя, определяется возвращающей силой - силой взаимодействия электрона с ядром атома.

Предположение, что переизлученное поле зависит от времени точно также как и поле падающей на среду волны, справедливо для линейной оптики. Эти поля отличаются только фазами и амплитудами. Сдвиг фаз между падающим и переизлученным полями в каждом атоме является причиной отличия фазовой скорости света в среде от скорости света в вакууме. Этим объясняется отличие от единицы показателя преломления: 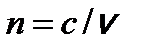. Потеря энергии при элементарном акте взаимодействия волны с атомом является причиной поглощения световой волны средой.

Дипольный момент, приобретенный атомом под действием световой волны, пропорционален напряженности поля волны при не слишком больших ее значениях: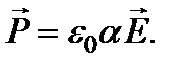

Коэффициент a называется линейной атомной восприимчивостью или коэффициентом поляризуемости. Вынужденное движение электронов среды в поле световой волны макроскопически проявляется в возникновении поляризованности среды, которая складывается из индуцированных электрическим полем волны дипольных моментов отдельных атомов, так что дипольный момент 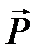, приобретенный 1м³ среды равен: ,

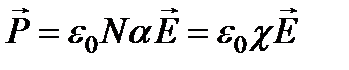где N - число атомов в единице объема, 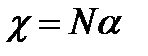- макроскопическая восприимчивость среды. Вводя вектор электрической индукции 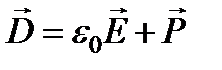, который связан с напряженностью 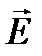электрического поля линейным материальным уравнением 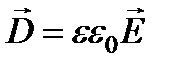, можно определить диэлектрическую проницаемость среды e, а, следовательно и показатель преломления немагнитной среды: , .

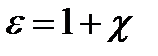Если отклик среды на световое поле определяется уравнением, т.е. пропорционален напряженности поля 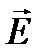, то поляризуемость атома и все оптические характеристики среды не зависят от интенсивности световой волны. Волны разных частот и направлений распространяются в среде независимо друг от друга, т.е. имеет место принцип суперпозиции.

В интенсивных лазерных пучках, напряженность электрического поля в которых сравнима с внутриатомными полями (E_а ~10¹¹ В/м), связь индуцированного дипольного момента уже не будет линейной, что проявится в зависимости оптических характеристик среды от интенсивности световой волны. В средах, свойства которых зависят от интенсивности или от напряженности поля нарушается принцип суперпозиции. Волны разных частот или разных направлений в нелинейной среде взаимодействуют между собой. Возникают и эффекты самовоздействия.

С нелинейными явлениями взаимодействия и самовоздействия все чаще приходится сталкиваться в современной лазерной оптике, акустике, физике плазмы. Нелинейные эффекты оказываются весьма существенными и при распространении мощных радиоволн в ионосфере.

Чтобы составить представление о линейной и нелинейной поляризуемости атома, запишем уравнение, которым описывается смещение из положения равновесия в поле световой волны. Для простоты речь идет об изотропной среде, где направление смещения электрона совпадает с направлением поля, ориентированного, например, вдоль оси Ox. В первом приближении, соответствующем линейной оптике, сила F, удерживающая электрон в положении равновесия, считается пропорциональной смещению электрона из положения равновесия, F = – kx, т.е. носит квазиупругий характер. Это соответствует квадратичной зависимости потенциальной энергии электрона от его смещения, U (x) = kx ²/2. В следующих приближениях нужно учесть члены более высокой степени в разложения U (x) в ряд по степеням смещения из равновесия

.

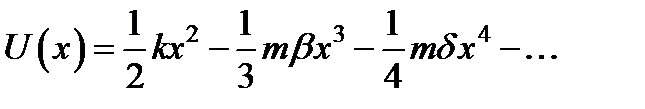Коэффициенты b, d определяются строением атома и обуславливают ангармонический характер движения (электрона) осциллятора. Нечетные степени в разложении U (x) могут быть только у систем без центра симметрии. В такой усовершенствованной модели уравнение движения электрона в пренебрежении затуханием принимает вид ,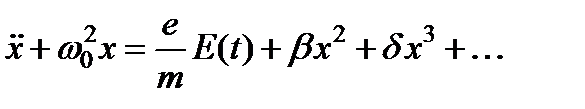

где - частота собственных колебаний при небольших амплитудах. Когда ангармонические члены bx ², dx ³, … имеют характер небольших поправок, уравнение можно решать методом последовательных приближений.

В нулевом приближении ангармонические члены отбрасываются и уравнение сводится к основному уравнению классической теории дисперсии линейной оптики, т.е. к уравнению движения линейного гармонического осциллятора: .

В монохроматическом поле 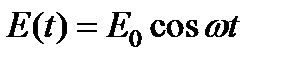его решение имеет вид: 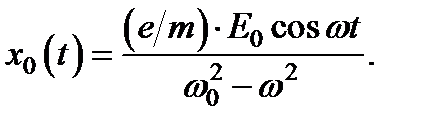Дипольный момент, приобретенный отдельным атомом под действием световой волны, пропорционален смещению электрона из положения равновесия (p = ex), что в сравнении с дает обычное выражение для линейной поляризуемости a ₀ = (e ²/ me ₀)/(w ₀² – w ²), не зависящее от напряженности электрического поля. Решение нулевого приближения x ₀(t) подставляется в ангармонические члены уравнения вместо x и в следующем приближении нужно решать линейное уравнение, в котором играющая роль вынуждающей силы правая часть содержит кроме cos wt гармонические составляющие на удвоенной и утроенной частотах: ,

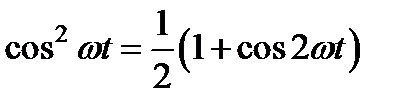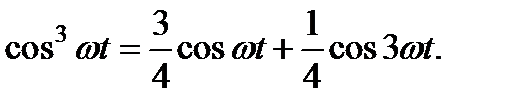
Поэтому и частное решение неоднородного уравнения, описывающее установившиеся колебания, кроме слагаемого x ₀(t) на основной частоте w содержит слагаемые с частотами 2 w, 3 w, …

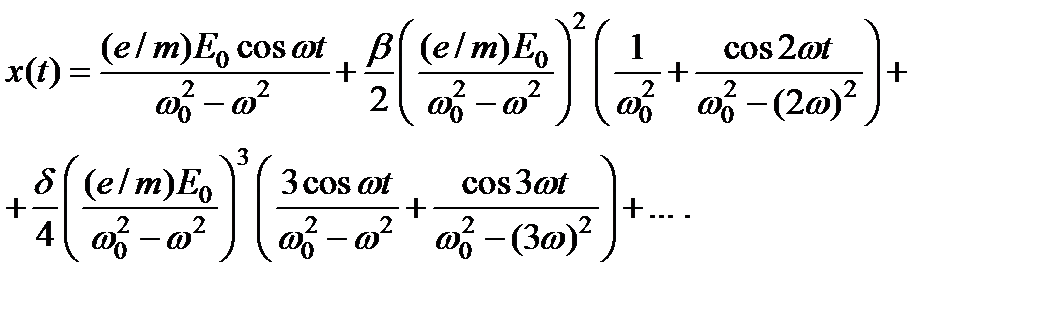
Следовательно, для ангармонических колебаний зависимость x (t) усложняется и становится нелинейной. Поэтому и поляризованность среды, которую можно представить в виде 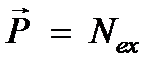, перестает быть линейной функцией от E. В сильных световых полях материальное уравнение, связывающее поляризованность среды с напряженностью электрического поля, становится нелинейным.

Для однородной анизотропной среды, без учета ее магнитных свойств и пространственной дисперсии, такое материальное уравнение в общем виде можно записать так:

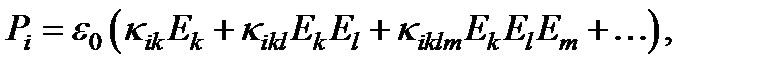
где в соответствии с общепризнанной символикой подразумевается, что по дважды повторяющимся индексам производится суммирование. i, k, l, m пробегают значения декартовых индексов. Тензор второго ранга k_ik представляет собой обычную (линейную) восприимчивость среды, а тензоры высших порядков k_ikl, k_iklm, … называются соответственно квадратичной, кубичной и т. д. Поле E в предполагается монохроматическим, а восприимчивости зависят от его частоты. Тензорный вид материального уравнения обусловлен тем, что для анизотропных сред направление вектора 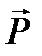в общем случае не совпадает с направлением вектора напряженности электрического поля 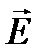. Если среда обладает центром симметрии, то все восприимчивости четных порядков обращаются в нуль (четность определяется числом индексов без первого). Так будет, например, в изотропной среде или кубических кристаллах. В таких средах невозможны эффекты, обусловленные восприимчивостями четных порядков.

При качественном описании нелинейных явлений можно воспользоваться упрощенной моделью среды, считая поляризованность параллельной напряженности поля и полагая в материальном уравнении восприимчивости всех рангов скалярами: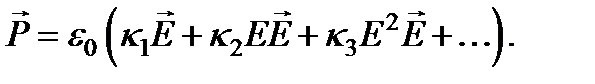

Надо только иметь в виду, что в кристаллах в выбранном направлении могут распространяться волны не всех, а только избранных поляризаций. Соотношение применимо к каждой из таких волн, причем для различных волн k ₁, k ₂, k ₃, … имеют различные значения.

Итак, на примере простой классической модели показано, что нелинейные восприимчивости появляются за счет ангармонических членов в потенциальной энергии оптического электрона. Электронный механизм появления нелинейности преобладает в твердых телах. Зависимость оптических характеристик среды от интенсивности световой волны может быть обусловлена не только влиянием поля волны на поляризуемость атома, но и воздействием на концентрацию и ориентацию атомов и молекул. В жидкостях эти факторы играют главную роль. Одна из причин локальных изменений концентрации молекул в световой волне связана с электрострикцией. Электрическое поле световой волны создает в среде всестороннее давление, пропорциональное квадрату напряженности поля. В результате сжатия возникают локальные изменения плотности среды (т.е. концентрации молекул), а следовательно, и показателя преломления.

Если молекулы среды анизотропны, т.е. поляризуемость молекул по разным направлениям различна, но при отсутствии внешнего поля все ориентации молекул равновероятны (что характерно для газов и жидкостей), то среда в целом будет изотропной. В сильных световых полях анизотропные молекулы ориентируются определенным образом относительно поля, и среда в оптическом отношении превращается в одноосный кристалл (так проявляется высокочастотный эффект Керра). Возникающая при этом нелинейность носит ориентационный характер.

Показатель преломления среды, кроме того, всегда изменяется из-за нагревания среды световой волной при ее поглощении. Во всех этих случаях проявляется зависимость оптических характеристик среды от интенсивности световой волны и все возможные механизмы возникновения нелинейности учитывает феноменологическое материальное уравнение.

Date: 2015-08-06; view: 1271; Нарушение авторских прав