Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Формулы Френеля
|
|
Рассчитаем амплитуды отраженной и преломленной волн. Предположим, что обе среды (однородные и изотропные) обладают нулевой проводимостью и, следовательно, совершенно прозрачны; их магнитные проницаемости фактически будут отличаться от единицы на пренебрежимо малые величины, и поэтому мы положим m 2 = m 1 = 1.
Пусть E 00 – амплитуда электрического вектора поля падающей волны, будем считать ее в общем случае комплексной величиной с фазой, равной постоянной части аргумента волновой функции. Переменная ее часть имеет вид:
,
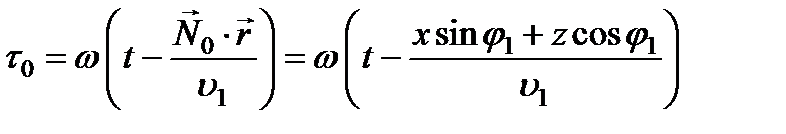где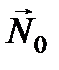 
- единичный вектор нормали к фронту волны.
Разложим каждый вектор на компоненты - параллельную (снабдим ее индексом ||) и перпендикулярную (индекс ^) плоскости падения. Выбор положительных направлений для параллельных компонент, указан на рис. 5.5. Перпендикулярные компоненты располагаются перпендикулярно к плоскости рисунка.
Тогда компоненты электрического вектора поля падающей волны запишутся в виде:
.
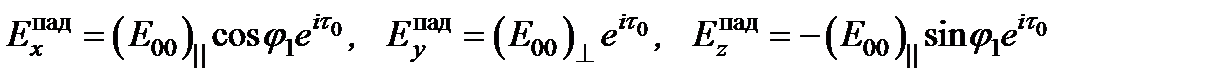Компоненты магнитного вектора сразу же получаются из соотношения (при m = 1)
.
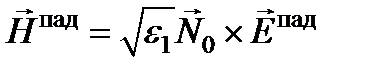Отсюда
,
,
.
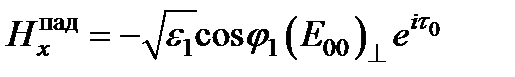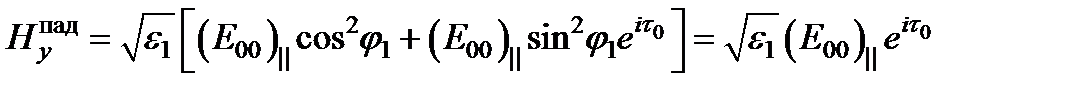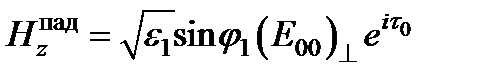Аналогично если E 20 и E 10 – комплексные амплитуды прошедшей и отраженной волн, то соответствующие компоненты электрического и магнитного векторов равны следующим величинам.
Поле волны отраженной:
; 
; 
; 
;
; 
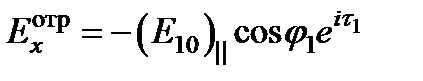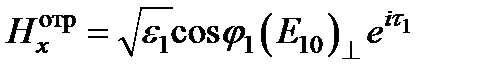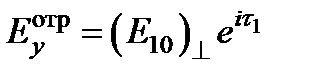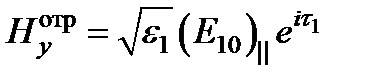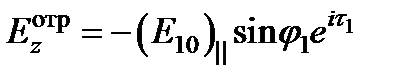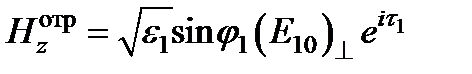,где
.
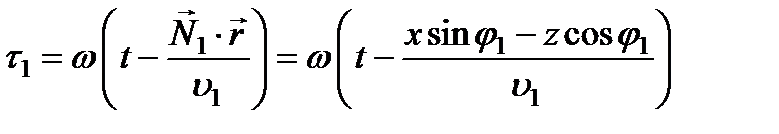Поле волны прошедшей: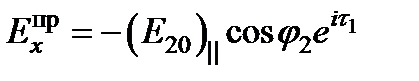 
; 
; 
; 
; 
; 
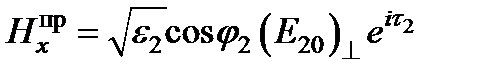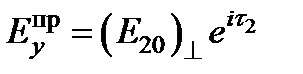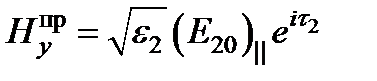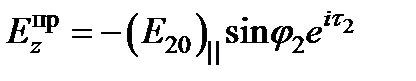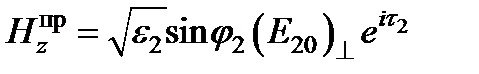,где
;
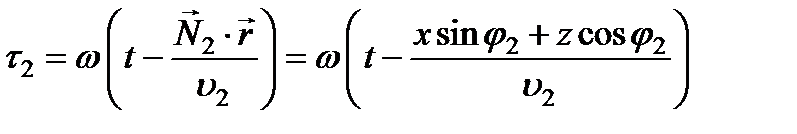Тангенциальные составляющие векторов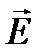 
и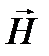 
должны быть непрерывны. Следовательно должны выполнятся соотношения: 
; 
; 
; 
.
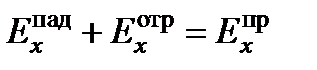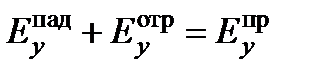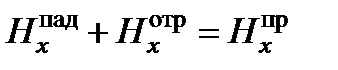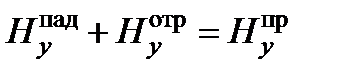При этом условия для нормальных компонент 
и 
будут удовлетворяться автоматически. Подставляя в значения всех компонент получим: (*)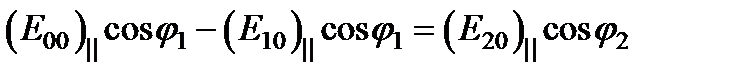 
; (**) 
; (**) 
; (*) 
.
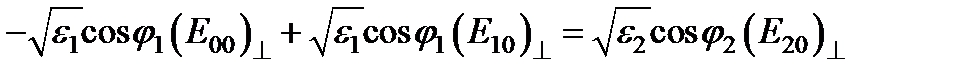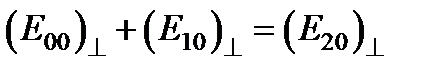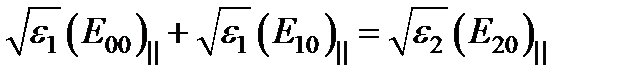Перепишем попарно формулы. В одной паре запишем только параллельные компоненты, а во второй – перпендикулярные:
(I)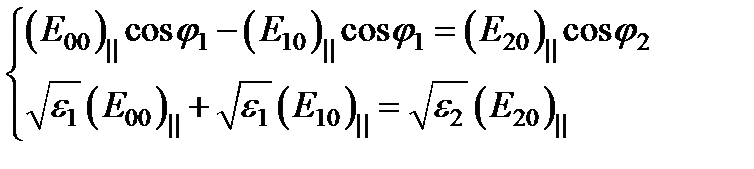 
;
(II)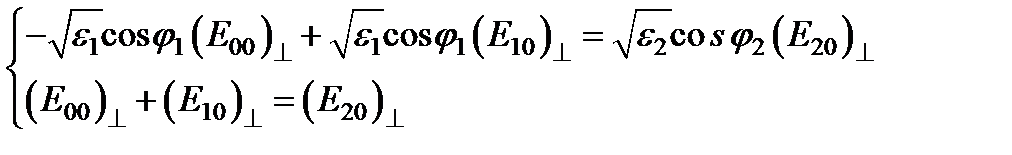 
.
Преобразуем пару (I):
(III)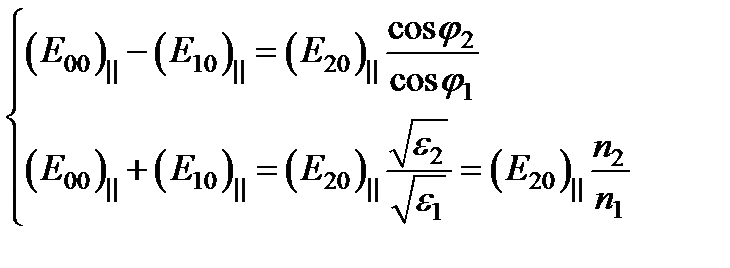 
.
Сначала сложим левые и правые части (III):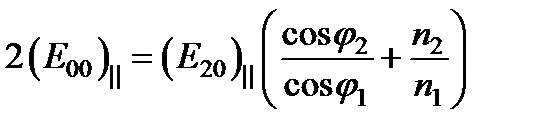 
.
Приведем к общему знаменателю и выразим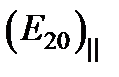 
: 
;
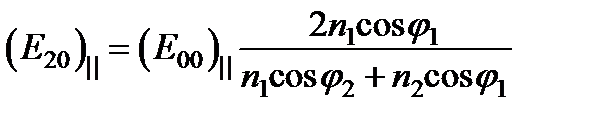- получили первую формулу Френеля.Теперь вычтем обе части (III):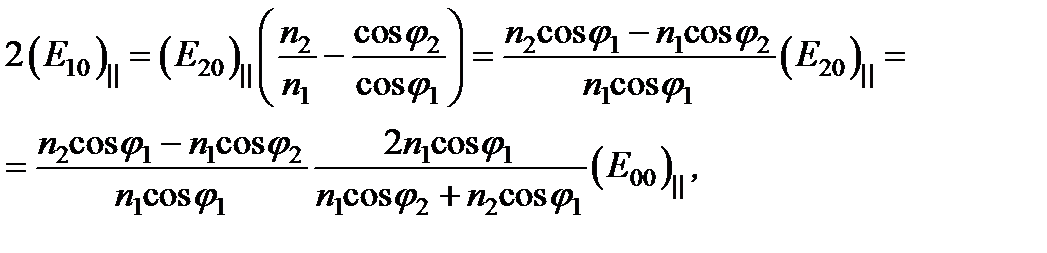 
откуда сразу же получаем вторую формулу Френеля: 
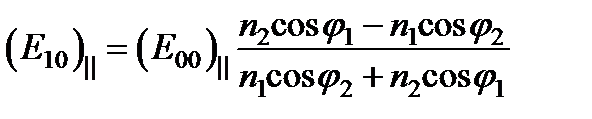. Эти соотношения пишутся обычно в другой форме, которую можно получить из и, используя закон преломления (5.48), а именно в форме 
; 
.
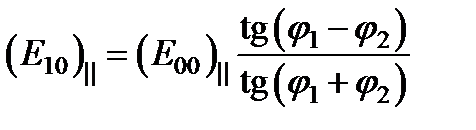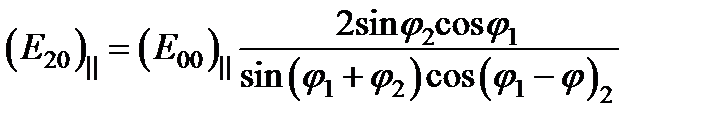Выполняя аналогичные преобразования со второй парой формул (11), содержащих перпендикулярные компоненты, получим еще две формулы Френеля
,
,
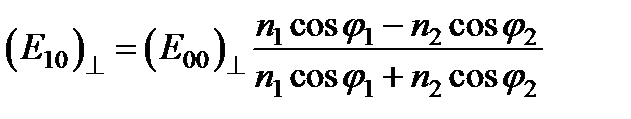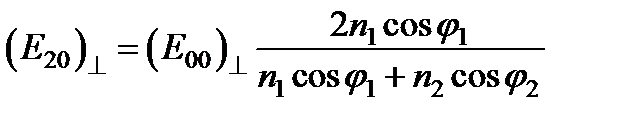которые могут быть записаны в другой форме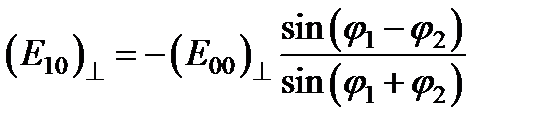 
, 
.
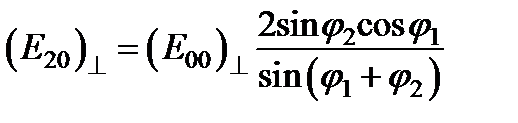Уравнения – называются уравнениями Френеля. Впервые они были введены Френелем в несколько менее общем виде в 1823 г. на основе его теории, рассматривавшей свет, как колебания упругой среды.
Date: 2015-08-06; view: 644; Нарушение авторских прав