
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

Анализ дисперсионной формулы
|
|
В изотропной однородной среде e (w), как и c (w),является скаляром и не зависит от пространственных координат. В случае комплексной восприимчивости c (w) диэлектрическая проницаемость также будет комплексной, что связано с учетом коэффициента затухания g. Тогда можно записать, что
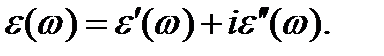
Введем комплексный показатель преломления по формуле  ,
,
где n - вещественный показатель преломления, c - показатель затухания.
Оба параметра зависят от частоты. Таким образом, получает принципиальное, хотя и формальное объяснение не только дисперсия (зависимость n (w)), но и поглощение, или абсорбция, света (зависимость c (w)).
Действительно, уравнение плоской монохроматической волны, распространяющейся, например, вдоль оси z в среде c комплексным показателем преломления может быть записано так:
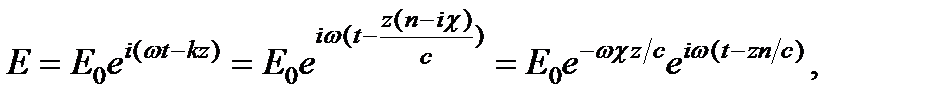
где 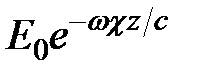 определяет амплитуду волны. Из полученного выражения следует, что действительная часть показателя преломления n, как и в случае прозрачной среды, определяет фазовую скорость волны: υ = c / n. Мнимая часть c характеризует ослабление волны по мере ее распространения (или убывание амплитуды). Так как интенсивность пропорциональна квадрату амплитуды световой волны, то в результате поглощения света интенсивность изменяется по закону:
определяет амплитуду волны. Из полученного выражения следует, что действительная часть показателя преломления n, как и в случае прозрачной среды, определяет фазовую скорость волны: υ = c / n. Мнимая часть c характеризует ослабление волны по мере ее распространения (или убывание амплитуды). Так как интенсивность пропорциональна квадрату амплитуды световой волны, то в результате поглощения света интенсивность изменяется по закону: 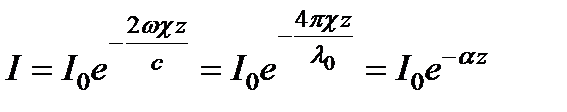 ,
,  .
.
Экспоненциальное уменьшение интенсивности по мере проникновения излучения в среду, выражаемое соотношением, называют законом Бугера. Величина a, называемая коэффициентом поглощения, характеризует быстроту этого уменьшения: на расстоянии h = 1/ a интенсивность уменьшается в e = 2,72 раза. В материалах, которые считают прозрачными, расстояние h (глубина проникновения) обычно много больше толщины образца.
Надо отметить, что если мнимая часть диэлектрической проницаемости отлична от нуля, то уменьшение интенсивности излучения обусловлено именно поглощением энергии и определяется paботой, совершаемой электрическим полем волны 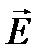 над поляризационными токами в веществе, плотность
над поляризационными токами в веществе, плотность 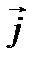 которых равна
которых равна 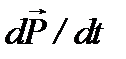 . Эта работа в единице объема за единицу времени равна
. Эта работа в единице объема за единицу времени равна 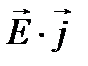 , и ее среднее значение отлично от нуля, когда мнимая часть восприимчивости c (и, следовательно, мнимая часть e) отлична от нуля.
, и ее среднее значение отлично от нуля, когда мнимая часть восприимчивости c (и, следовательно, мнимая часть e) отлична от нуля.
Затухание волны не обязательно должно быть связано с истинным поглощением электромагнитной энергии. Если диэлектрическая проницаемость вещественна, но отрицательна, то коэффициент c будет отличен от нуля. Фактически это означает, что излучение при e ²(w) = 0 и e ¢(w) < 0 не может проникнуть в вещество и на данной границе происходит полное отражение волны.
Возведем теперь выражение в квадрат и сравним действительные и мнимые части полученного соотношения и соотношения. Тогда получим: 
где для упрощения записи дальнейших формул введена константа wр согласно определению
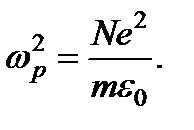
Она характеризует модель среды и имеет размерность частоты.
При частотах w, близких к собственной частоте w 0, в формулах возможны упрощения: при w = w 0 всюду, кроме (w 02 – w 2), можно заменить w на w 0, a (w 02 – w 2) преобразовать следующим образом:
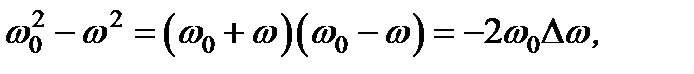
где D w = w – w 0. В результате формулы принимают вид:  ,
,  .
.
Попытка получить из формул зависимость n (w) и c (w) в явном виде приводит к очень громоздким выражениям. Сравнительно простые выражения для n (w) и c (w) получаются, если сделать еще одно упрощающее предположение. Будем считать среду настолько разреженной, что максимальное значение nc в, которое достигается при D w = 0, мало по сравнению с единицей, т.е.  . Тогда и максимальное значение второго слагаемого в выражении (
. Тогда и максимальное значение второго слагаемого в выражении (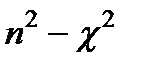 ) много меньше единицы. Пренебрегая членами, квадратичными по малому параметру wp 2/(4 w 0 g), из находим
) много меньше единицы. Пренебрегая членами, квадратичными по малому параметру wp 2/(4 w 0 g), из находим  ;
; 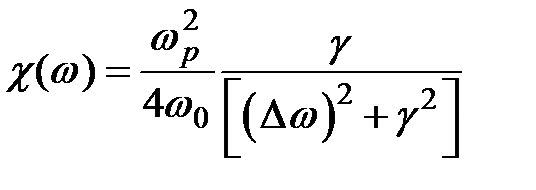 .
.
Благодаря простому виду этих формул можно проанализировать их физическое содержание. Такой анализ позволит и для общего случая составить качественное представление о характере зависимости от частоты показателей преломления и затухания вблизи линии поглощения.
Графики функций (n (w)-1) и χ (w) приведены на рис. 5.3.
| A |
| D |
| C |
| B |

Р и с. 5.3
Зависимость показателя преломления от частоты n (w) называют дисперсионной кривой. Зависимость показателя затухания от частоты χ (w) характеризует спектральный контур линии поглощения. В рассматриваемой модели среды, состоящей из неподвижных затухающих осцилляторов, зависимость χ (w) имеет максимум при D w = 0, т.е. при w = w 0. Ширина максимума на половине высоты равна 2 g и растет с увеличением постоянной затухания.
Показатель преломления сначала растет с увеличением частоты (отрезок АВ), достигая максимального значения при D w = – g, т.е. при w = w 0 – g. Затем n (w) убывает при возрастании частоты (отрезок ВС) и после перехода через центр линии поглощения становится меньше единицы. Минимум n (w) расположен при D w = g (т.е. при w = w 0 + g). При дальнейшем увеличении частоты показатель преломления возрастает (отрезок СD), асимптотически приближаясь к 1.
Уменьшение показателя преломления при увеличении частоты, которое происходит в пределах ширины спектрального контура линии поглощения, называют аномальной дисперсией. Она должна наблюдаться у всех веществ в тех областях спектра, где имеется сильное поглощение.
При частотах, далеких от собственной частоты w 0 атомных осцилляторов, где выполняется условие 2 wg << | w 02 – w 2|, мнимой частью в можно пренебречь. Тогда для зависимости показателя преломления от частоты получаем следующую приближенную формулу:
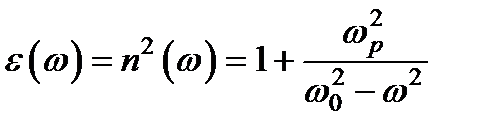 .
.
При тех значениях частоты, для которых эта формула применима, показатель преломления возрастает с увеличением частоты. Такой характер зависимости n (w) называют нормальной дисперсией.
Для низких частот (w < w 0) показатель преломления больше единицы, т.е. фазовая скорость c / n волны в среде меньше скорости света в вакууме. Это значит, что измененная средой волна отстает по фазе от падающей. Это условие выполняется, например, при распространении видимого излучения в прозрачных веществах (стекло, кварц). Собственные частоты атомных осцилляторов этих веществ лежат в ультрафиолетовой части спектра.
Если же частота излучения больше собственной частоты осциллятора (w > w 0), то n < 1 и фазовая скорость волны в среде (υ = c / n) оказывается больше скорости света в вакууме, т.е. измененная волна по фазе опережает падающую. Но никакого противоречия с теорией относительности здесь нет, так как теория относительности утверждает, что скорость материальных тел и скорость сигнала не могут превышать скорость света в вакууме. Понятия показателя преломления и фазовой скорости применимы к монохроматической волне, имеющей бесконечную протяженность в пространстве и во времени. Монохроматическая волна не может служить для передачи сигнала.
Приближение (w > w 0) можно использовать для описания дисперсии в стекле рентгеновского излучения, частота которого в несколько тысяч раз больше частоты видимого света. Очевидно, что здесь n < 1, хотя и мало отличается от 1, так как в данном случае частота w велика. Формально такой же результат получается и при описании совершенно иного явления: распространения радиоволн в ионосфере. Ионосфера представляет собой полностью ионизованный газ (плазму), в которой излучающие электроны не связаны внутриатомными силами. Можно положить w 0 = 0, и для таких "свободных" электронов условие w >> w 0 будет выполняться даже в области низкочастотных колебаний paдиодиапазона. Формула принимает в этом случае вид:
 .
.
Теоретические соображения, изложенные выше, справедливы не только для электронов, но и для ионов, и притом классические представления для них более обоснованы ввиду относительно больших масс ионов. Кроме того, во всех телах, даже в одноатомных газах с одним оптическим электроном, имеется не одна, а несколько полос поглощения. Чтобы учесть это, в классической модельной теории предполагается, что вещество построено из частиц различного типа - электронов и ионов, которые ведут себя как затухающие гармонические осцилляторы с различными собственными частотами и коэффициентами затухания. Пренебрегая в газах их взаимодействием, формулу для дисперсии можно представить так: 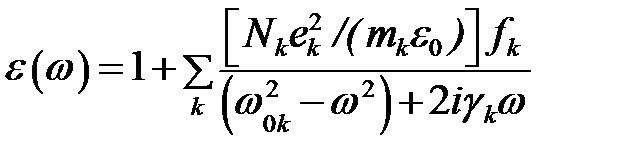 ,
,
где Nk, mk, ek, w 0 k, gk - концентрация, масса, заряд, собственная частота и коэффициент затухания осциллятора k -го типа. Каждой собственной частоте соответствует своя линия поглощения, вблизи которой показатель преломления меняется аномально. Общий ход показателя преломления в зависимости от частоты представлен схематически на рис. 5.4. Величина fk, входящая в формулу и называемая силой или эффективностью отдельных сортов осцилляторов, вводится для согласования с опытом, притом
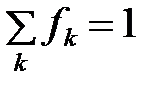 .
.
Классическая дисперсионная формула дли газов с большой точностью описывает фактически наблюдаемый ход показателя преломления вблизи отдельных линий поглощения w 0 k, но лишь при условии, что коэффициенты Nk, а также собственные частоты w 0 k и коэффициенты затухания gk рассматриваются как эмпирические постоянные, определяемые из самой кривой дисперсии и фактического положения спектральных линий в спектре излучения или поглощения вещества.

Р и с. 5.4
К такой же дисперсионной формуле приводит и квантовая теория, в которой, однако, параметры w 0 k и fk приобретают вполне определенный физический смысл. Согласно квантовым представлениям, атом при отсутствии внешних полей может находиться только во вполне определенных стационарных состояниях, в которых его энергия может принимать также вполне определенные дискретные значения E 1, E 2,... (уровни энергии). При переходе атома из одного состояние в другое происходит испускание (или поглощение) света c частотой, определяемой правилами Бора: 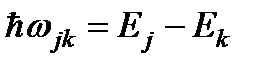 .
.
При переходе атома с высшего энергетического уровня на более низкий уровень происходит излучение света с испусканием кванта энергии. При обратном переходе атома с низшего энергетического уровня на более высокий уровень происходит возбуждение атома с поглощением кванта энергии. Т.о., в отличие от классического гармонического осциллятора, атом, даже если он одноэлектронный, излучает (или поглощает) не одну частоту w 0, а целый спектр частот wjk, которые в квантовой теории дисперсии и играют роль собственных частот атома.
Сила осциллятора в квантовой теории тоже приобретает ясный физический смысл; она оказывается пропорциональной вероятности перехода из k -го в j -ое состояние. Чем больше эта вероятность, тем большая часть из имеющихся в k -ом состоянии атомов перейдет за единицу времени в j -ое состояние, т.е. тем эффективнее данный переход участвует в явлении.
Date: 2015-08-06; view: 1198; Нарушение авторских прав