Классическая электронная теория дисперсии

В данной теме будет рассмотрено действие поля световой волны на движение связанных в атоме заряженных частиц. Решение этой задачи позволит понять разнообразные физические явления, истолкование которых было невозможно с позиций классической электромагнитной теории света.

Соединение электромагнитной теории света и электронных явлений является заслугой нидерландского ученого Лоренца Х. А. Появлению этой фундаментальной теории предшествовал ряд наблюдений, опытов и попыток их обобщения.

В первую очередь рассмотрим дисперсию вещества, т.е. зависимость показателя преломления от длины волны проходящего света (или зависимость от длины волны фазовой скорости распространения электромагнитных волн). Напомним, что еще Ньютон поставил опыт (разложил белый цвет в спектр), наглядно иллюстрирующий зависимость n = n (l) (рис. 5.1).

Р и с. 5.1 Р и с. 5.2

Впоследствии, изучая преломление света в призмах, наполненных молекулами красителя, было обнаружено, что эта зависимость принимала более сложный вид (рис. 5.2).

Существует интервал длин волн, где поведение n аномально. Отрезок AB и CD, где dn / dl < 0 соответствует нормальной дисперсии. Отрезок BC, где dn / dl > 0 – описывает аномальную дисперсию.

Для описания нормальной дисперсии, исходя из упругостной теории света, была предложена формула Коши: 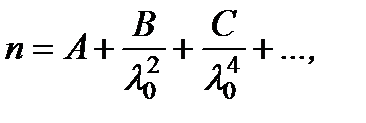где A, B, C и т.д. – постоянные, l ₀ – длина волны в вакууме.

Обычно ограничиваются первыми двумя членами, так что: 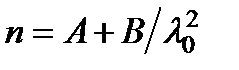. Скорость изменения показателя преломления с изменением длины волны (dn / dl) называют дисперсией вещества, которая характеризует свойства вещества. Все среды, за исключением абсолютного вакуума, обладают дисперсией.

Феноменологическая теория Максвелла, не содержащая никаких атомно-молекулярных констант, не давала объяснения дисперсии света. Для этого необходимы атомистические представления. Дисперсия света возникает в результате вынужденных колебаний заряженных частиц – электронов и ионов – под действием переменного поля электромагнитной волны. В классической теории Лоренца строение колеблющихся систем – атомов и молекул - и их колебания описываются на основе классических представлений о движении и законов Ньютона.

При распространении электромагнитных волн в среде электрическая составляющая поля волны вызывает колебательные движения электронов и ядер, входящих в состав атомов и молекул среды. Колеблющиеся электроны и ядра сами становятся источниками вторичных электромагнитных волн той же частоты. Эти вторичные волны налагаются друг на друга и вместе с падающей волной образуют полное результирующее поле в среде. Эффект сложения падающей волны с вторичными волнами эквивалентен изменению фазовой скорости волны в веществе. Отношение фазовой скорости распространения волны в вакууме к скорости распространения ее в данной среде определяет численное значение показателя преломления данной среды, который является одной из важнейших ее характеристик.

На возбуждение колебаний электронов и ядер электромагнитная волна затрачивает часть энергии. В идеальной однородной среде вторичные волны полностью отдают поглощенную долю энергии, которая была затрачена на возбуждение колебаний. В реальном веществе не вся энергия колеблющихся электронов и ядер испускается обратно в виде электромагнитных волн, а часть ее переходит в другие формы энергии и, главным образом, в тепловую. Потерю энергии световым пучком, проходящим сквозь вещество, вследствие превращения ее в различные формы внутренней энергии вещества называют поглощением света.

Рассмотрим более подробно процесс взаимодействия электромагнитного поля волны с веществом. Как известно, подобное рассмотрение может быть проведено как в классическом, так и в квантовом приближении. Мы остановимся лишь на классическом подходе к рассмотрению взаимодействия излучения с веществом.

Макроскопическая теория взаимодействия излучения с веществом исходит из некоторой идеализированной модели строения вещества. Наибольшей простотой отличается модель газообразной среды, так как для нее в первом приближении можно не учитывать взаимодействия атомов или молекул и, кроме того, можно считать, что действующее на отдельный атом поле совпадает со средним полем в веществе. В таких условиях для получения макроскопического материального уравнения достаточно рассмотреть действие поля волны на изолированный атом.

Входящие в состав атома электроны можно разделить на внешние, или оптические, и электроны внутренних оболочек. С излучением оптического диапазона взаимодействуют практически только внешние электроны, поэтому их называют оптическими электронами. Собственные частоты электронов внутренних оболочек столь велики, что поле световой волны на них практически не влияет и лишь для рентгеновского излучения внутренние электроны становятся существенными.

При возбуждении атома (или смещении электрона из положения равновесия) со стороны частей этого атома и окружающих атомов будет действовать сила, стремящаяся вернуть электрон в положение равновесия, так что электрон будет совершать гармонические собственные колебания с определенной частотой. Как показывает опыт, изолированные атомы всех веществ способны испускать практически монохроматические волны с характерными для каждого вещества частотами, поэтому можно предположить, что сила, удерживающая электрон в положении равновесия или сила связи оптического электрона с атомом носит характер упругой силы и зависимость ее от смещения электрона (при условии, что это смещение невелико) определена законом 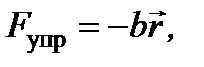где r - величина смещения электрона, b - соответствующая константа упругой связи.

Применяя к электрону в атоме законы классической механики, можно записать уравнение движения электрона (массы т), смещенного из положения равновесия и предоставленного действию этой внутриатомной силы, которая носит упругий характер 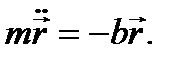Из уравнения следует, что

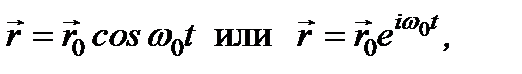
где r ₀ - амплитуда колебаний, w ₀² = b / m - круговая частота собственных колебаний электрона, причем w ₀ зависит от природы атома, определяющей величину константы b (значение w ₀ получено из уравнения после подстановки в него второй производной по времени от смещения электрона).

Собственная частота w ₀ атомного электрона может быть рассчитана только на основе квантовой теории атома. В рамках классической теории ее следует рассматривать как формально введенную постоянную.

Предположение о гармоническом характере колебаний электрона в атоме имеет лишь приближенный характер. В действительности же, электрон, приведенный в колебание, постепенно отдает свою энергию, и, следовательно, амплитуда колебания с течением времени уменьшается. Поэтому колебание атома не имеет строго гармонического характера и должно рассматриваться как затухающее. Даже в случае изолированного атома колебания будут затухающими, ибо энергия будет покидать атом, излучаясь во все стороны (радиационное затухание).

Кроме затухания, неизбежно связанного с излучением, могут иметь место и другие причины растраты колебательной энергии, связанные с взаимодействием атомов между собой, причем в этих случаях энергия колебания может переходить и в другие формы (например, в тепло) увеличивая среднюю кинетическую энергию хаотического движения атомов среды.

Затухание колебаний можно описать, вводя в уравнение движения излучающего заряда эффективную силу трения (сопротивления) 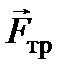таким образом, чтобы потеря энергии на излучение могла быть представлена как средняя работа этой силы, хотя никаких сил сопротивления в обычном смысле этого слова здесь нет.

Сила эта, как показывает опыт, обычно мало искажает собственные колебания атомов, так что растраченная за период энергия составляет лишь ничтожную часть колебательной энергии атома. При таких условиях можно учесть эту силу, положив ее пропорциональной скорости движения электрона:

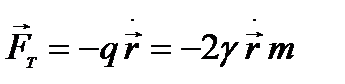, где коэффициент q зависит от природы вещества.

В классическом приближении ядро атома в паре с каждым оптическим электроном можно моделировать затухающим гармоническим осциллятором, характеризуемым определенной собственной частотой w ₀ и постоянной затухания g. А в целом, атом моделируется совокупностью гармонических осцилляторов с соответствующими собственными частотами и постоянными затухания.

Предполагаемая модель затухающего гармонического осциллятора, которая описывает поведение оптического электрона, выглядит чрезмерно упрощенной в свете современных представлений о строении атома. В атомных масштабах движение электрона подчиняется законам квантовой, а не классической физики. Никаких квазиупругих сил и сил трения, пропорциональных скорости, в атомах нет. Строение атомов и молекул определяется кулоновскими силами взаимодействия электронов и ядер. Но классическая физика оказалась не в состоянии объяснить на основе этих сил структуру и даже само существование атомов и молекул как устойчивых образований. Более точное описание атома дает только квантовая механика. Для описанной выше модели гармонического осциллятора квантовая теория некоторых явлений, в частности, дисперсии и поглощения света, приводит к тем же результатам, что и классическая, хотя и с некоторыми особенностями, которые мы отметим.

Пусть в среде распространяется монохроматическая световая волна, длина волны которой должна быть много больше среднего расстояния между атомами или молекулами среды. Заряженные частицы, входящие в состав атома, и в первую очередь, электроны испытывают воздействие со стороны электрического и магнитного поля этой волны. Это воздействие эквивалентно проявлению некоторой вынуждающей силы. Так как магнитное поле действует только на движущийся заряд, а скорость его пренебрежимо мала по сравнению со скоростью света, то магнитной силой можно пренебречь и ограничиться учетом действия лишь электрического поля волны, т.е. на электрон будет действовать вынуждающая сила 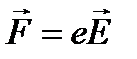, где 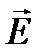- напряженность электрического поля.

В разреженных газах, где расстояние между молекулами среды велико и можно пренебречь действием окружающих молекул, поляризованных проходящей световой волной, действующее поле можно заменить полем световой волны. Уравнение движения электрона в поле световой волны, с учетом ранее оговоренных сил, имеет вид .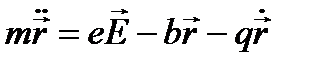

Оно представляет собой уравнение движения при вынужденных колебаниях. Разделив все члены выражения на массу электрона m и учитывая, что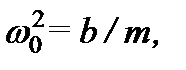

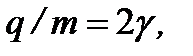
приведем предыдущее уравнение к виду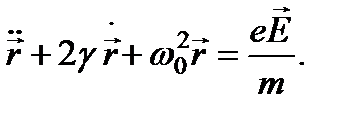

Зависимость напряженности электрического поля плоской монохроматической волны от координат и времени может быть записана так: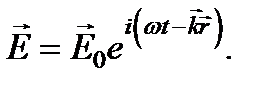

В пределах элемента объема, малого по сравнению с длиной волны, электрическое поле волны можно считать однородным и изменяющимся со временем по гармоническому закону:

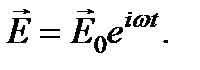
Нас будет интересовать не общее, а только частное решение уравнения, представляющее установившиеся вынужденные колебания электронов, частота которых совпадает с частотой вынуждающей силы. Поэтому решение уравнения для смещения электрона можно искать в виде: 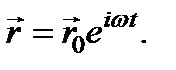Амплитуду вынужденных колебаний 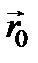найдем, подставляя r и его производные, а также действующее поле в уравнение. В результате получим: .

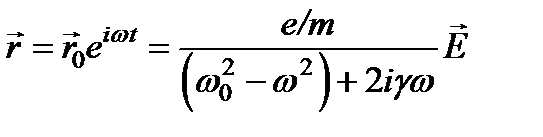Смещение электрона из положения равновесия в электрическом поле световой волны проявляется в том, что атом в электрическом поле приобретает дипольный момент, пропорциональный напряженности поля в случае изотропной среды: .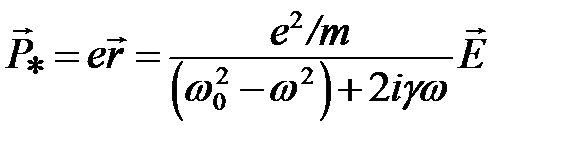

Зависящий от w коэффициент пропорциональности между 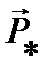и 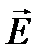в формуле называется атомной поляризуемостью a (w):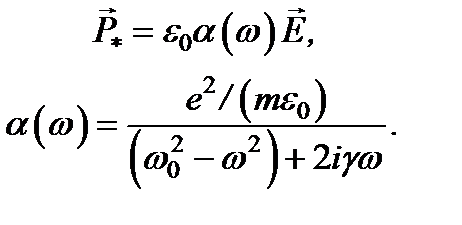

Если в единице объема среды находится N атомов одного сорта и в каждом из них способен смещаться только один электрон, то электрический момент 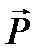единицы объема, или поляризованность вещества, будет равен 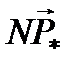или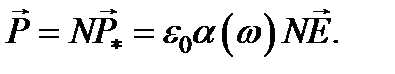

С другой стороны, если амплитуда 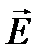напряженности поля волны много меньше напряженности внутриатомных электрических полей, то отклик вещества на поле можно считать линейным. Это значит, что поляризованность среды в пределах рассматриваемого элемента объема однородна и изменяется по гармоническому закону с частотой внешнего воздействия w и амплитудой, пропорциональной :

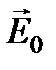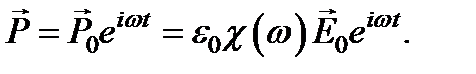
Направление вектора 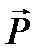в изотропной среде, где нет физически выделенных направлений, совпадает с направлением вектора 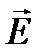. Коэффициент пропорци-ональности c (w) между 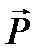и 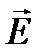, называемый диэлектрической восприимчи-востью, в изотропной среде является скаляром. Сравнивая выражения и видим, что .

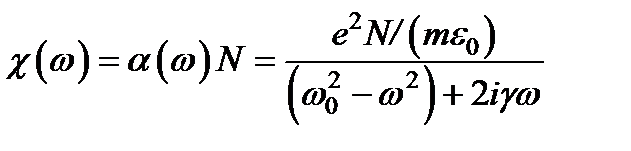При вынужденных колебаниях электронов вещества под действием электрического поля волны движение электронов, создающее поляризованность, в общем, происходит с отставанием по фазе от колебаний напряженности электрического поля. Это запаздывание по фазе проявляется в том, что восприимчивость c (w) – комплексная величина. Когда затуханием элементарных осцилляторов можно пренебречь, отставания по фазе не будет и восприимчивость выражается вещественной величиной. Так будет для частот, далеких от собственной частоты осцилляторов, т.е. в спектральной области прозрачности среды.

Восприимчивость, характеризующая распространение монохроматической волны, зависит от частоты волны w. Об этой зависимости говорят как о законе дисперсии восприимчивости. Вид функции c (w) определяется структурой вещества.

Если ввести вместо напряженности электрического поля 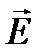, вектор электрической индукции согласно, то уравнениям Максвелла для электромагнитных волн в веществе можно формально придать такой же вид, как и для вакуума. Поскольку вектор 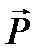из дальнейшего рассмотрения такой заменой исключается, то целесообразно вместо функции восприимчивости c (w), связы-вающе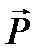й и 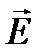, ввести диэлектрическую проницаемость e (w), связывающую век-торы и 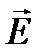в монохроматической волне:

.

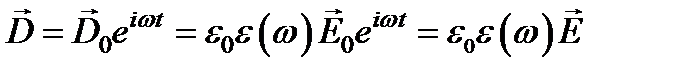Подставляя в значения 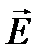и 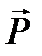, определяемые соответственно выражениями и, получим связь между e (w) и c (w): e (w) = 1 + c (w)

или с учетом выражения получим окончательное решение упрощенной задачи дисперсии и абсорбции (поглощение) света: .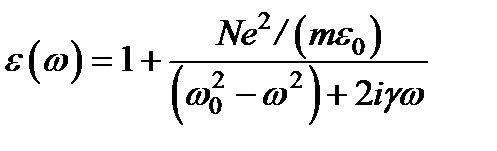

Date: 2015-08-06; view: 624; Нарушение авторских прав