Классификация голограмм

Голограмма отображает практически все характеристики волновых полей – амплитуду, фазу, спектральный состав, состояние поляризации, изменение волновых полей во времени, а также свойства волновых полей и сред, с которыми эти поля взаимодействуют.

Внутри голографии определился ряд различных направлений ее развития, каждое из которых соответствует определенной разновидности голограмм и её свойствам.

Свойства голограмм весьма разносторонни и вовсе не сводятся к одной только способности записывать и восстанавливать волновые поля.

В зависимости от геометрической конфигурации светочувствительной среды, в которой зарегистрирована интерференционная картина, различают двумерные и трехмерные голограммы (объёмные). В первом случае толщина фотоматериала h много меньше пространственного периода d регистрируемой интерференционной картины. Отображающие свойства двумерной голограммы ограничены. В частности, она неоднозначно восстанавливает волновое поле излучения объекта: кроме истинной объектной волны и соответствующего ей истинного изображения объекта в этом случае восстанавливается ложная, так называемая сопряженная волна и соответствующее ей ложное сопряженное изображение. Источник света, с помощью которого восстанавливается двумерная голограмма, должен быть строго монохроматичным, поскольку (в силу отсутствия селективных свойств) двумерная голограмма восстановит все соответствующие разным l изображения, и, как следствие этого, результирующее изображение будет сильно размыто. Двумерные голограммы используются при решении задач радио-, акустической и цифровой голографии, при голографическом распознавании образцов, а также в некоторых других случаях.

Трехмерная голограмма, у которой толщина h много больше d, представляет собой наиболее общий случай голографической записи. Она однозначно восстанавливает волновое поле объекта. Особенностью такой голограммы является также способность воспроизводить не только фазу и амплитуду записанного на ней излучения, но и его спектральный состав. Если такую голограмму восстановить источником излучения со сплошным спектром, то она сама выберет из сплошного спектра те составляющие, которые участвовали в ее записи. Трехмерность записи особенно выявляется в оптическом диапазоне спектра, когда длина волны регистрируемого на голограмме излучения, как правило, намного меньше толщины светочувствительного материала.

Чтобы показать, как геометрия получения голограммы влияет на её дифракционные свойства, рассмотрим интерференцию сферической волны, исходящей из точечного источника S, находящегося на определенном расстоянии от регистрирующей среды, и опорной плоской волны, распространяющейся сверху вниз, как показано на рис. 4.47. Точечный источник представляет собой элементарный объект, а сферическая волна, исходящая из него, – предметную волну. Заметим попутно, что более сложный объект можно рассматривать как совокупность элементарных точечных источников, свет от каждого из них интерферирует с опорной волной.

Р и с. 4.47

На рис. 4.47 представлено одно из поперечных сечений семейства поверхностей максимальной интенсивности, образующихся при интерференции плоской опорной волны и предметной волны от точечного источника. В нашем случае следами поверхностей являются параболы.

На рисунке обозначены некоторые характерные положения пластинки при регистрации голограммы. Габор, не имевший в своем распоряжении лазера и вынужденный максимально использовать свет от источников с низкой когерентностью при получении своих голограмм помещал пластинку в положение 1. Здесь направление света от точки S и направление опорной волны почти коллинеарны, поэтому полученные таким образом голограммы были названы голограммами с осевым опорным пучком, или осевыми голограммами. Разность хода предметной и опорной волн в этом случае минимальна, это позволяет использовать источники с низкой когерентностью. Относительно большое расстояние между соседними поверхностями максимумов снижает требования к разрешающей способности регистрирующей среды.

Лейт и Упатниекс получили внеосевые голограммы с таким взаимным расположением пучков, которое эквивалентно помещению голографической пластинки в положение 2.

Благодаря использованию лазерного света в их установке разность хода в предметном и опорном пучках могла иметь большую величину. Такое расположение позволяет преодолеть трудности, которые возникают при осевых голограммах, а большая когерентность лазерного света позволяет восстанавливать трехмерные изображения. Именно этот результат привлек внимание к голографии и способствовал ее возрождению.

В положении 2 среднее направление света от точечного источника образует острый угол с направлением опорной волны. Если толщина регистрирующей среды мала по сравнению с расстоянием между поверхностями максимумов, то голограмма, полученная в этом положении, действует как двумерная дифракционная решетка. Падающий луч может в этом случае взаимодействовать только с одной поверхностью при прохождении через среду. Следовательно, голограмма представляет собой систему линий на поверхности. То же самое справедливо и для габровских осевых голограмм.

Для голограмм получаемых в положении 3, угол между средним направлением света от точечного источника и направлением плоской волны составляет приблизительно 90° и расстояние между соседними поверхностями интерференционных максимумов имеет меньшую величину. Если толщина голограммы больше этого расстояния, то регистрирующую пластинку можно рассматривать как объемную дифракционную решетку. Такую решетку можно представить как ряд частично отражающих плоскостей, селективный отклик которых на падающий свет соответствует закону Брэгга. Голограммы, зарегистрированные в положении 3, получили название брэгговских. На рис. 4.48 показана (в разрезе) объемная дифракционная решетка, содержащая периодически расположенные рассеивающие (отражающие) плоскости, освещенные плоской волной. Р и с. 4.48

Интенсивность имеет максимальную величину в том направлении, в котором происходит синфазное сложение световых волн, рассеянных последовательными плоскостями. Условие образования главного максимума дифрагированной плоской волны, которое имеет вид ,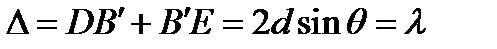

называется законом Брэгга по имени ученого, получившего его для случая дифракции рентгеновских лучей от атомных плоскостей в кристалле. Брэгг предположил, что дифракция в кристалле обусловлена отражением падающей волны от кристаллических плоскостей. Максимум дифракции возникает, когда углы, образованные падающим и отраженным лучами с кристаллической плоскостью равны, как показано на рис. 4.48, причем угол q удовлетворяет условию.

На рис. 4.49 представим в разрезе плоскую дифракционную решётку. Решётка может состоять из ряда периодически расположенных прозрачных и непрозрачных линий на экране. Для плоской волны, падающей на решетку, условие синфазности дифрагированных пучков, ведущее к их взаимному усилению, является уравнением решетки 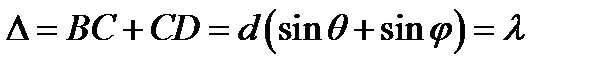, где d – постоянная решётки, q – угол падения и j – угол дифракции. При выполнении условия под углом j образуется главный максимум дифрагированной плоской волны. Р и с. 4.49

Сравнение выражений и показывает, что условие накладывает более жесткие условия на наблюдение максимума дифракции. Для объемной решетки выбор угла падения определяет и угол дифракции, и длину волны. Для плоских решеток это не так, поскольку уравнение допускает произвольный выбор и угла падения и длины волны.

Селективные свойства брэгговской дифракции дали возможность получить первые голограммы, дающие многоцветное изображение.

В положении 4 (рис. 4.47) плоская волна падает на голографическую пластинку с одной стороны, а сферическая – с другой. Период интерференционной картины составляет примерно l /2, и поверхности максимальной интенсивности почти параллельны поверхности голографической пластинки. Получение голограмм в этом положении впервые описал Денисюк. Если интерференционная картина регистрируется в галоидосеребряной эмульсии, то в ней образуется большое число близко расположенных частично отражающих серебряных плоскостей, которые действуют как отражательный интерференционный фильтр. Даже в эмульсии с толщиной лишь 12-15 мкм может образоваться около 50-100 серебряных слоев. Поскольку эти слои подобны слоям, образующимся в методе цветной фотографии Липмана, и, поскольку дифракция на них происходит в соответствии с законом Брэгга, такие голограммы называют голограммами Липпмана-Брэгга-Денисюка. Их еще называют отражательными. Селективность такой голограммы позволяет восстанавливать предметную волну в белом свете,

Заметим, что голограммы характеризуются не только углом, который составляет предметный и опорный пучки при их регистрации. Существуют голограммы Фурье, фраунгоферовские голограммы, голограммы сфокусированных изображений и другие разновидности голограмм.

Date: 2015-08-06; view: 1287; Нарушение авторских прав