Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?
Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника
Тонкие линзы
|
|
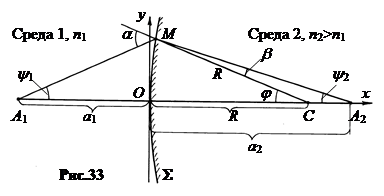
1. Преломление света на сферической поверхности. Пусть две среды с показателями преломления n 1 и n 2 разделяются сферической поверхностью S. Если из точки A 1, лежащей на главной оптической оси поверхности, выходит узкий гомоцентрический пучок лучей, то, преломившись на поверхности, он сходится в точке A 2 (полагаем n 2 > n 1). Найдем связь между расстоянием a 1 от предмета A 1 до вершины поверхности точки O, между расстоянием a 1 от вершины поверхности O до изображения A 2 и радиусом кривизны поверхности R.
Рассмотрим один луч A 1 MA 2, где M – точка на поверхности, в которой луч преломляется (рис.33). По теореме синусов в треугольниках A 1 MC и MCA 2 имеем:
, 
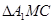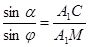, (6.1)
, 
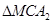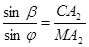, (6.2)
Разделим 1-е уравнение на 2-е.
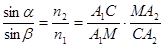. (6.3)
Полагаем пучок лучей параксиальным. В этом случае с учетом правила знаков A 1 M = A 1 O = -a 1, MA 2 = OA 2 = a 2, MC = OC = R, A 1 C = –a 1 + R, CA 2 = a 2- R. Уравнение (6.3) принимает вид: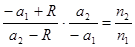 
. (6.4)
Избавившись от дробности и разделив на a 1 a 2 R, получаем: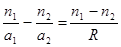 
. (6.5)
Это формула преломляющей сферической поверхности. Интересно, что при n 2 = - n 1 она переходит в формулу сферического зеркала.
Из формулы (6.5) следует, что любой луч, вышедший из точки A 1, при малых углах y 1 независимо от положения точки преломления M придет в одну и ту же точку A 2. Сферическая преломляющая поверхность преобразует один гомоцентрический пучок в другой.
2. Фокусы сферической преломляющей поверхности. Если на сферическую границу падает пучок лучей, параллельных главной оптической оси, например слева, то - a 1 = ∞. Отсюда находим a 2: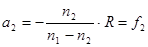 
. (6.6)
Если пучок падает справа, то a 2 = ∞, и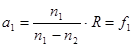 
. (6.7)
Величины f 1 и f 2 определяют расстояния от вершины поверхности O до точек F 1 и F 2, в которых сходятся параллельные пучки. Точки F 1 и F 2 – это фокусы преломляющей поверхности, а f 1 и f 2 – фокусные расстояния.
3. Тонкая линза. Оптически прозрачное тело, ограниченное двумя гладкими кривыми поверхностями, называется линзой. Бывают цилиндрические, сферические, конические и другие линзы. Рассмотрим сферическую линзу с радиусами кривизны поверхностей R 1 и R 2. Полагаем, слева по рис.34 от линзы находится среда 1 с показателем преломления n 1, справа от линзы – среда 2 с показателем преломления n 2. Вещество самой линзы имеет показатель преломления n.
Полагаем линзу тонкой, то есть считаем, что толщина ее O 1 O 2 мала по сравнению с радиусом кривизны поверхностей линзы R 1 и R 2. Это значит, что точки O 1 и O 2 совпадают с точкой O, называемой оптическим центром линзы.
Все лучи, проходящие через точку O, не меняют своего направления и называются осями линзы. Ось, проходящая через центры кривизны поверхностей точки c 1 и С 2, называется главной оптической осью линзы, остальные – побочными осями.
4. Формула тонкой линзы. Найдем связь между расстоянием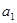 
от линзы до светящейся точки A 1, расстоянием a 2 от линзы до изображения этой точки A 2 и параметрами линзы R 1 и R 2 и сред n 1, n 2, n.
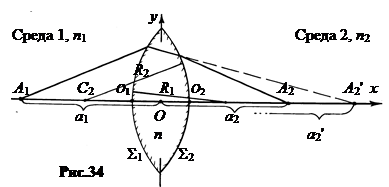Преломление лучей на первой сферической поверхности S1 создало бы без второй сферической поверхности S2 в сплошной среде с показателем преломления n изображение A 2' на расстоянии a 2' от вершины O. Так что из формулы (6.5) следует: 
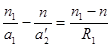.(6.8)
Для второй поверхности S2 изображение A 2' является мнимым источником света. Построение изображения этого источника A 2' после преломления на поверхности S2 дает точку A 2 на расстоянии a 2 от линзы. Так что можно записать:
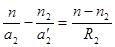. (6.9)
Просуммировав оба выражения, получаем формулу линзы.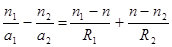 
. Общая формула линзы. (6.10)
5. Фокусы линзы. При падении параллельного пучка слева, когда a 1 = -∞, получаем фокусное расстояние справа от линзы f 2, а при падении пучка справа, когда a 2 = +∞, получаем фокусное расстояние f 1 слева от линзы.
, 
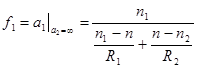. (6.11)
В подавляющем большинстве практических случаев линза находится в однородной среде с показателем преломления n 1. Тогда n 2 = n 1, и формула линзы упрощается. Так как обычно n > n 1, то формулу удобно записать так: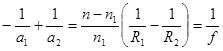 
. (6.12)
Здесь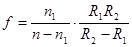 
- фокусное расстояние линзы. (6.13)
Если линза находится в однородной сфере, то фокусы линз слева и справа удалены на одинаковое расстояние f. Если n > n 1, то линза, более толстая в средине, называется собирающей. Ее фокусное расстояние положительно, f > 0, а фокус действительный (рис.35).
Линза, более толстая по краям, чем в середине, называется рассеивающей. Ее фокусное расстояние отрицательно, f < 0, а фокус мнимый (рис.36).
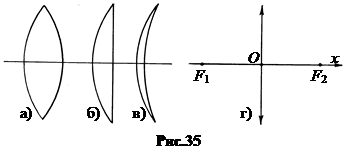На рис.35 показаны сечения разных типов собирающих линз: двояковыпуклая (а), плосковыпук-лая (б), мениск (в). На чертежах собирающие линзы изображаются отрезком со стрелками на концах и с точками главных фокусов (рис.35-г).
Типы рассеивающих линз пока-заны на рис.36: двояковогнутая (а), плосковогнутая (б), мениск (в). Схема-тическое изображение на рис.36-г.
Величина, обратная фокусному расстоянию линзы, называется ее оптической силой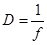 
. (6.14)
Единица измерений D называется диоптрия (дптр). Линза с фокусным рас-стоянием f = 1 м имеет оптическую силу D = 1 дптр, с f = 0,5 м – D = 2 дптр и так далее. У собирающих линз D > 0, у рассеивающих D < 0. Наиболее часто в диоптриях определяют оптическую силу очковых линз.
6. Построение изображений в собирающих линзах выполняется с помощью трех лучей: луча 1, проходящего через оптический центр не преломляясь, луча 2, идущего параллельно главной оптической оси, а после линзы – через задний фокус F 2, и луча 3, идущего через передний фокус F 1, а после линзы – параллельно главной оптической оси.
Различают 3 случая.
а. Предмет находится от линзы дальше двойного фокусного расстояния (рис.37). Изображение действительное, перевернутое, уменьшенное.
б. Предмет находится между двойным и главным фокусами линзы (рис.38). Изображение действительное, перевернутое, увеличенное. По сравнению с первым случаем предмет и изображение меняются местами.
в. Предмет находится между главным фокусом и линзой (рис.39). Изображение мнимое, прямое и увеличенное. Этот случай соответствует использованию линзы в качестве лупы.
7. 
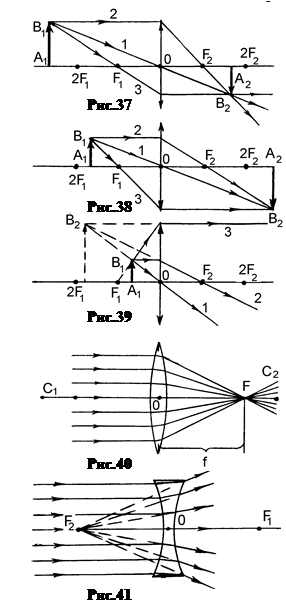Построение изображения в рассеивающих линзах. Пучок лучей, параллельных главной оптической оси, пройдя собирающую линзу, сходится в точке заднего главного фокуса F 2 (рис.40). Такой же пучок лучей, прошедший рассеивающую линзу, расходится. Через фокус рассеивающей линзы идут не сами лучи, а их продолжения, построенные в обратном ходу лучей направлении (рис.41). Поэтому если задний фокус F 2 собирающей линзы находится справа, то у рассеивающей линзы он находится слева. Справа находится передний фокус F 1.
Независимо от расстояния до предмета во всех случаях получается мнимое, уменьшенное, прямое изображение, расположенное между предметом и линзой (рис.42).
8. 
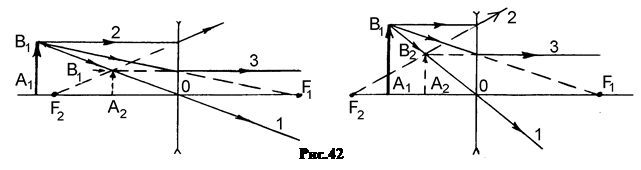Построение изображения точки A 1, лежащей на главной оптической оси, делается с помощью произвольного луча 1, вышедшего из точки A 1, вспомогательного параллельного луча 2, проходящего через оптический центр линзы не преломляясь. Этот вспомогательный луч 2 позволяет определить направление преломленного луча 1 после выхода из линзы.
 |
В собирающей линзе луч 1 идет так, чтобы пересечься со вспомогательным в фокальной плоскости заднего фокуса (рис.43), а в рассеивающей линзе так, чтобы со вспомогательным лучом в фокальной плоскости заднего фокуса пересеклось его продолжение (рис.44).
Пересечение самого луча 1 или его продолжения с главной оптической осью и дает изображение A 2. В первом случае действительное, во втором – мнимое.
9.
 |
Если показатель преломления вещества линзы меньше показателя преломления окружающей среды, n < n 1, то знаки фокусных расстояний меняются. Выпуклая линза становится рассеивающей (рис.45), а вогнутая – собирающей (рис.46).
Date: 2015-08-06; view: 1400; Нарушение авторских прав