Световые измерения. Энергетические величины

1. Энергетические величины. Поскольку свет есть объективный процесс переноса в пространстве энергии ЭМ поля, то он может характеризоваться величинами, не зависящими от свойств человеческого глаза. В основу таких величин положена энергия. Поэтому они называются энергетическими.

Различают энергетические характеристики световой волны, характеристики источника света, характеристики светящейся или освещенной поверхности.

2. Характеристики световой волны. Их две: интенсивность и поток энергии.

a. Интенсивность света I _s – это средняя за период энергия, переносимая ЭМ волной через единичную площадку, ориентированную нормально к направлению распространения волны. Иначе, это средняя за период мощность волны 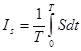. (2.1)

Здесь T – период волны, S – вектор Умова – Пойнтинга, t – время.

Найдем зависимость интенсивности от напряженности электрического поля волны. Так как S = W ₀ v, где W ₀ – плотность энергии ЭМ поля, а v – скорость волны, и приняв во внимание, что средние за период слагаемые в выражении W ₀ одинаковы получаем:

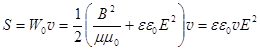. (2.2)

Но 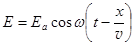. Интенсивность света измеряется в определенной точке пространства, где x = const. Полагаем для простоты x = 0. Получаем:

. (2.3)

Так как 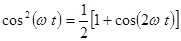, то (2.4)

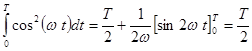. (2.5)

Отсюда, 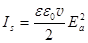. (2.6)

Интенсивность света пропорциональна квадрату амплитуды светового вектора.

Из формулы Максвелла 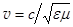, где c – скорость света в вакууме. Магнитная проницаемость m оптически прозрачных сред практически не отличается от единицы, m»1. Величина 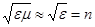(2.7)

называется абсолютным коэффициентом (показателем) преломления среды.

Скорость волны в среде v = cçn (2.8)

тем меньше, чем больше показатель преломления среды.

Подставив формулу (2.8) в выражение (2.6), получаем: . (2.9)

Единица измерения интенсивности Вт/м².

б. Поток энергии Ф – это энергия, переносимая ЭМ волной через произвольную поверхность 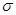за единицу времени. 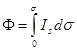. (2.10)

Единица измерения потока энергии Ф - ватт (Вт).

3. Плоские и телесные углы. Цель настоящего пункта - напомнить особенности этих геометрических понятий.

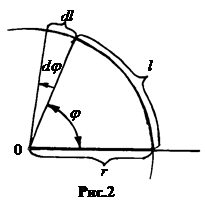
Плоский угол есть угловая мера двумерного плоского пространства. Угол j между двумя лучами, вышедшими из одной точки О (вершины угла) определяется отношением длины l дуги окружности с центром в точке O к радиусу окружности r (рис.2), j = lçr. (2.11)

Единица измерения плоского угла радиан (рад). Это угол, опирающийся на дугу, равную по длине радиусу. 1 рад = (l=r)çr. Внесистемная единица - градус, 1 рад = 57,3°. Полный плоский угол, опирающийся на всю длину окружности, включает 2 p = 6,26 радиан.

Телесный угол есть угловая мера трехмерного пространства. Величина телесного угла W определяется отношением поверхности S сегмента шара, заключенном в этом телесном угле, к квадрату радиуса r шара (рис.3-а), W = Sçr ². (2.12)

Единица телесного угла называется стерадианом (ср). Стерадиан – это угловое простран-ство конуса с вершиной в центре шара радиусом r, опирающегося на часть поверхности сферы площадью r ²: 1 ср = (S=r ² )çr ².

Полный телесный угол равен отношению площади поверх-ности шара к квадрату его радиуса, W_полн = 4 pr ² çr ² = 4 p = 12,57.

Координатные плоскости прямоугольной декартовой системы делят весь телесный угол на 8 частей (октантов), равных 4 p½ 8= p½ 2 = 1,57 ср.

В тех случаях, когда требуется интегрирование телесного угла, надо знать его элементарное выражение d W. По определению, d W = dSçr ², где dS - площадь элементарного сегмента сферы, на которую опирается телесный угол d W. Как видно из рис.3-б, эта площадь dS (на рисунке заштрихована) приближается к прямоугольнику и может быть представлена как произведение сторон. dS = AB×АC = [ r sin j× dq ]×[ r× dj ].

Здесь j – полярный угол, 0 ≤ j ≤ p, q – азимутальный угол, 0 ≤ q ≤ 2 p.

Отсюда .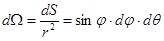

4. Характеристики точечного источника света. Таких характеристик всего одна. Она называется силой излучения.

Сила излучения I источника света определяется отношением потока энергии Ф, создаваемого источником в телесном угле W, к величине этого телесного угла. 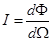.(2.13)

Численно сила излучения источника равняется потоку энергии, излучаемому источником в единичном телесном угле. Единица силы излучения [ I ] = Вт/ср.

Если известна сила излучения источника, то поток энергии, излучаемый источником в произвольном телесном угле, в общем случае найдется интегрированием.

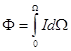. (2.14)

Если источник изотропный, то есть излучает по всем направлениям одинаково, то величина I выносится из-под знака интеграла. Тогда F = I W. (2.15)

В полном телесном угле поток энергии от такого источника составляет F = 4 p I. (2.16)

Найдем связь между силой излучения I точечного источника и интенсивностью I _s излучаемой им волны. Если источник изотропный, то полный поток энергии F = 4 pI. С другой стороны, этот же поток можно представить как произведение интенсивности волны I _s на расстоянии r от источника на поверхность сферы радиуса r.

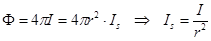. (2.17)

Интенсивность световой волны от точечного источника пропорциональна его силе излучения и обратно пропорциональна квадрату расстояния до источника.

5. Характеристики протяженного источника. Точечный источник – это идеализация. Реальные источники света имеют конечные размеры, которыми не всегда можно пренебречь. Источником излучения в этом случае является поверхность излучающего тела. Она характеризуется двумя величинами – энергетической яркостью и энергетической светимостью.

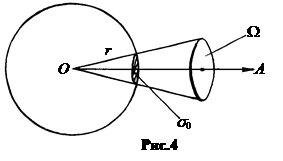
a. Энергетическая яркость поверхности B. Пусть излучающим телом является одинаково излучающий по всем направлениям шар радиуса r (рис.4). Поток энергии, создаваемый этим шаром, как и в случае точечного источника равен Ф = 4 pI. Но в отличие от точечного источника здесь I – сила излучения, создаваемая поверхностью s ₀ в направлении нормали OA. Отношение Içs ₀= B ₀ называется яркостью поверхности в направлении нормали.

Так как 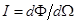, то 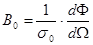. (2.18)

С увеличением радиуса r излучающего шара площадь излучающей поверхности s ₀ растет. Поэтому яркость поверхности B ₀ при F = const уменьшается.

В общем случае излучающая поверхность может быть расположена под произвольным углом j к направлению излучения (рис.5). В этом случае величина s ₀ определяется как проекция излучающей поверхности s на плоскость, нормальную к направлению излучения, s ₀ = s × cos j. Формула яркости в общем случае принимает вид:

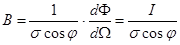. (2.19)

Энергетическая яркость поверхности B определяется численно величиной потока энергии, излучаемой единичной проекцией излучающей поверхности в данном направлении в пространстве единичного телесного угла.

Если излучение поверхности обусловлено нагретостью тел (спираль электрической лампы накаливания, поверхность Солнца, пламя), то в основном оно является диффузным. Яркость таких поверхностей не зависит от угла j. В честь основоположника фотометрии Иоганна Ламберта (1728 – 1787) такие светящиеся поверхности называют ламбертовыми.

Сила излучения диффузно светящейся поверхности с постоянной площадью s = const найдется из формулы (2.19).

I = Bs cos j= I ₀×cos j. Закон Ламберта, 1760. (2.20)

Здесь Bs = I ₀ – сила излучения площадки s в направлении нормали.

Уменьшение силы излучения диффузно излучающей поверхности постоянной площади s с ростом угла j обусловлено уменьшением проекции излучающей поверхности.

Если излучение поверхности обусловлено отражением света, то оно является часто селективным (избирательным). Например, зеркальные поверхности полированных металлов. А шероховатые поверхности таких диэлектриков как бумага, молочное стекло, порошки минералов и другие приближаются к ламбертовым поверхностям и в отраженном свете.

Единица измерения энергетической яркости 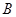- Вт ç (ср×м²).

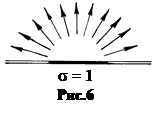б. Энергетическая светимость R численно равна потоку энергии, который излучается единичной поверхностью в пространстве телесного угла 2 p (рис.6).

Найдем связь между яркостью B ламбертовой поверхности и ее светимостью R.

Пусть произвольная площадка s с яркостью B излучает в направлении угла j в телесном угле d W, как следует из формулы (2.19), поток d F = Bs cos jd W. Поток во всем угловом полупространстве W = 2 p найдется интегрированием.

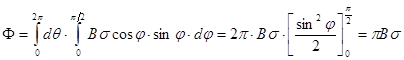. (2.21)

Здесь j – полярный угол, изменяется от 0 до p½ 2, q – азимутальный угол, 0 ≤ q ≤ 2 p.

Разделив на величину площадки s, получаем поток F, излучаемый единичной площадкой в угловом пространстве 2 p, то есть светимость.

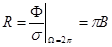. (2.22)

Единица измерения энергетической светимости Вт/м².

6. Освещенная поверхность характеризуется одной величиной – энергетической освещенностью.

Энергетическая освещенность E численно равна потоку энергии, падающему на единичную площадку освещаемой поверхности. 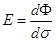. (2.23)

При освещении точечным источником поток d F, падающий на поверхность ds, есть d F = Id W где I – сила излучения источника. Тогда E = d F çds = I×d W çds. (2.24)

Телесный угол d W, в котором распространяется поток d F, равен отношению сегмента сферы ds ₀ к квадрату расстояния до источника r ² (рис.7), d W = ds ₀ çr ² = ds ×cos jçr ². Подставив d W çds = cos jçr ² в формулу (2.24), получаем закон освещенности от точечного источника: 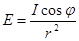. Закон освещенности. (2.25)

Освещенность поверхности пропорциональна силе излучения источника I, косинусу угла между направлением на источник и нормалью к площадке, и обратно пропорциональна квадрату расстояния до источника. Единица измерения энергетической освещенности Вт/м².

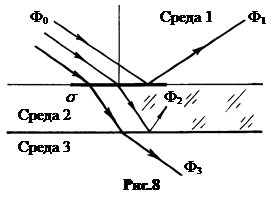
7. Коэффициенты отражения, поглощения и пропускания. Пусть на поверхность s толстой пластинки падает поток излучения F₀ (рис.8). В результате взаимодействия излучения с пластинкой часть энергии отразится (поток F₁), часть энергии поглощается (поток F₂) и часть энергии проходит сквозь пластинку (поток F₃). Отношение потоков называют:

F₁ ç F₀ = r (ро) – коэффициент отражения по интенсивности;

F₂ ç F₀ = a (альфа) – коэффициент поглощения по интенсивности;

F₃ ç F₀ = t (тау) – коэффициент пропускания по интенсивности.

Отношения потоков к поверхности есть:

F₀ ç s = E – энергетическая освещенность,

F₁ ç s = R ₁ – энергетическая светимость поверхности в среде 1,

F₃ ç s = R ₃ – энергетическая светимость поверхности в среде 3.

Date: 2015-08-06; view: 1258; Нарушение авторских прав