Зеркала

1. Зеркало – это гладкая поверхность, способная отражать падающие на нее лучи. В зависимости от формы поверхности различают плоские, сферические, цилиндрические, параболические и другие зеркала. Наиболее употребительны зеркала с плоской и сферической поверхностью.

2. Сферические вогнутые зеркала. Их важнейший геометрический параметр – радиус кривизны R.

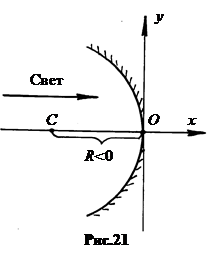
Для графического построения изображений сферическое зеркало (сегмент отражающей сферической поверхности) располагается в центре прямоугольной системы координат так, чтобы центр кривизны точка C находился на оси OX, а одна из точек поверхности – в начале системы координат в точке O (рис.21). Отражающая сторона зеркала располагается так, чтобы падающие на зеркало лучи шли в положительном направлении оси OX.

Поскольку отражающая поверхность обладает осевой симметрией относительно оси OX, то для построений достаточно сечения зеркала координатной плоскостью XOY.

Точка O, лежащая на отражающей поверхности зеркала на оси OX, называется вершиной зеркала, а ось, проходящая через вершину O и центр зеркала C – главной оптической осью зеркала. При таком расположении зеркала главной оптической осью является ось OX.

Все отрезки на оси OX, откладываемые вправо от точки O, имеют положительные значения. Аналогично, отрезки на оси OY положительны выше точки O и отрицательны ниже. Из этого правила знаков следует, что радиус кривизны вогнутого зеркала R - отрицательное число.

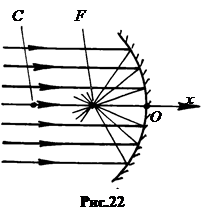
3. Фокус сферического зеркала. Пусть на вогнутое зеркало падает пучок лучей, параллельных главной оптической оси. Если пучок параксиальный (от греч. para’ – возле, axial – ось), то есть лучи идут близко к главной оптической оси, то после отражения от зеркала все лучи параксиального пучка пересекаются в одной точке F, лежащей на главной оптической оси (рис.22). Эта точка 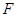называется главным фокусом зеркала.

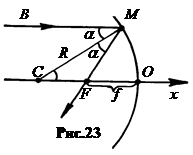
Найдем расстояние от вершины зеркала точки 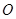до главного фокуса F. Для этого рассмотрим ход одного из лучей, параллельных оси OX (рис.23).

Пусть луч падает на зеркало в точку M. Угол a между падающим лучом и радиусом, проведенным в точку M, есть угол падения. По закону отражения угол FMC равен углу CMB.

Так как падающий луч по условию параллелен главной оптической оси OX, то углы BMC и MCF равны как накрест лежащие. Следовательно, в треугольнике FMC углы MCF и FMC одинаковы. Треугольник FMC равнобедренный. Стороны MF и FC одинаковы.

Если точку M устремить к главной оптической оси OX, то отрезок MF перейдет в пределе в отрезок OF. Отсюда следует, что отрезки OF и FC одинаковы.

Расстояние f от вершины зеркала O до главного фокуса F называют главным фокусным расстоянием зеркала. Так как отрезок OC = R есть радиус кривизны зеркала, то очевидно, что f = Rç 2. Поскольку радиус кривизны вогнутого зеркала R при таких знаковых условиях отрицательное число, то и его фокусное расстояние f так же отрицательное число, R < 0, f < 0.

4. Фокальная плоскость. Пучок параллельных лучей, падающих на зеркало под углом y к главной оптической оси, после отражения также собирается в одной точке F', которая находится несколько в стороне от главного фокуса F (рис.24). При небольших углах y эта точка лежит в фокальной плоскости. Так называется плоскость, перпендикулярная главной оптической оси OX и проходящая через главный фокус F.

Чтобы найти построением точку F', где соберется наклонный пучок, достаточно рассмотреть один луч, тот, что проходит через центр кривизны точку C. Тогда пересечение этого луча с фокальной плоскостью и есть точка F'.

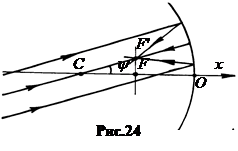
5. Формула сферического зеркала. Пусть на главной оптической оси вогнутого зеркала находится светящаяся точка A ₁. Лучи, испущенные точкой A ₁, отразившись от зер-кала, пересекутся в точке A ₂, находящейся на главной оптической оси (рис.25). Светящуюся точку A ₁ называют предметом, а точку A ₂– оптическим изображением точки A ₁.

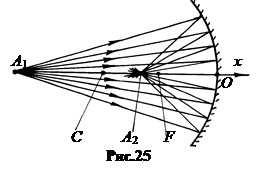Пучок лучей, расходящийся из одной точки или сходящийся в точку, называется гомоцентрическим (от греч. homo’s – общий). Сферическое зеркало преобразует один гомоцентрический пучок в другой.

Найдем связь между тремя отрезками: расстоянием a ₁ от вершины зеркала точки O до предмета A ₁, расстоянием a ₂ от вершины зеркала до изображения A ₂ и фокусным расстоянием f. Поскольку все три отрезка с учетом принятого правила – отрицательные числа, то при записи соотношений в треугольниках будем записывать их со знаком «минус».

Выделим один произвольный луч, идущий из точки предмета A ₁, и после отражения от зеркала в точке M приходящего в точку изображения A ₂ (рис.26).

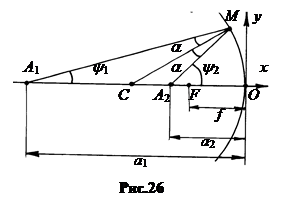Рассмотрим два треугольника A ₁ MC и CMA ₂. По теореме синусов для каждого из них запишем:

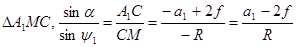, (5.1)

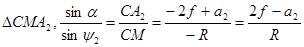, (5.2)

Разделим первое уравнение на второе.

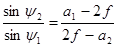(5.3)

Условие параксиальности лучей требует, чтобы углы y ₁ и y ₂ не превышали 5 - 7°. В этом случае с точностью до 3 знаков sin y ₁ = tg y ₁, sin y ₂ = tg y ₂, а точку отражения M можно полагать находящейся на оси OY. Если вертикальная координата точки M есть y, то sin y ₁ = tg y ₁ = yç-a ₁, sin y ₂ = tg y ₂ = yç-a ₂. Уравнение (5.1) принимает вид:

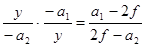, или fa ₂ + fa ₁ = a ₁ a ₂ (5.4)

Разделив на произведение a ₁ a ₂ f, получаем: 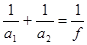. (5.5)

Это формула сферического зеркала, справедливая и с учетом правила знаков.

6. Построение изображений в вогнутом сферическом зеркале. Пусть точка предмета B ₁ не лежит на главной оптической оси. Для построения ее оптического изображения применяют обычно 3 луча. Они дают возможность построить изображение любой точки, пользуясь лишь линейкой.

Различают 3 случая: предмет находится от зеркала дальше центра кривизны точки C, предмет находится между центром кривизны точкой C и главным фокусом F и предмет находится между вершиной O и главным фокусом зеркала F.

a. Предмет A ₁ B ₁ находится от зеркала дальше центра кривизны точки C (иногда говорят, дальше двойного фокуса, рис.27-а).

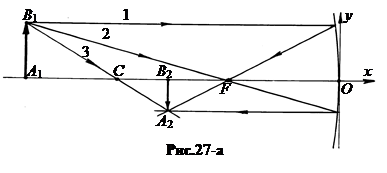Луч 1 идет параллельно главной оптической оси, после отражения от зеркала идет через главный фокус F.

Луч 2 идет вначале через главный фокус F, а после отражения идет параллельно главной оптической оси.

Луч 3 идет через центр кривизны C туда и обратно.

Изображение A ₂ B ₂ полу-чается действительным (каждая точка оптического изображения образуется пересечением лучей), перевернутым, уменьшенным.

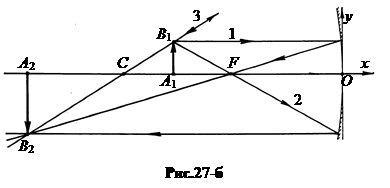
б. Предмет A ₁ B ₁ находится между главным фокусом F и центром кривизны C (рис.27-б). изображение A ₂ B ₂ получается действительным, перевернутым, увеличенным. По сравнению с первым случаем предмет и изображение меняются местами.

в. Предмет A ₁ B ₁ находится между вершиной зеркала O и главным фокусом F (рис.27-в). Все три луча, вышедшие из точки B ₁, после отражения от зеркала расхо-дятся и не могут нигде пересечься. Поэтому действительного изображе-ния точки они дать не могут.

Однако, если этот расходящийся пучок лучей попадает в глаз или объектив фотоаппарата, то любая оптическая система будет воспринимать этот пучок как бы вышедшим из некоторой точки B ₂, находящейся на продолжении отраженных лучей за зеркалом. Такое оптическое изображение, которое образовано продолжением отраженных лучей, называют мнимым. Изображение A ₂ B ₂ предмета в этом случае получается мнимым, прямым, увеличенным.

г. Построение изображения точки A ₁, лежащей на главной оптической оси, с помощью одной линейки невозможно, если пользоваться только вышедшими из этой точки лучами. Задача решается так.

Из точки предмета A ₁ строит-ся произвольный луч 1 до зеркала. Затем строится параллельный вспомогательный луч 2, идущий через центр кривизны C. Поскольку лучи параллельны, они пересекутся в фокальной плоскости. Следовательно, луч 1, отразившись от зеркала, пойдет так, что пересечется со вспомогательным лучом в фокальной плоскости (рис.28). Пересечение луча 1 с главной оптической осью дает изображение A ₂.

7. 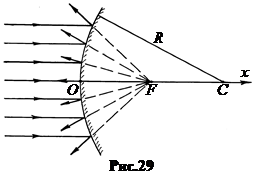Выпуклые сферические зеркала имеют положительный радиус кривизны R > 0 и мнимый фокус. Если на выпуклое зеркало падает пучок лучей, параллельных главной оптической оси, то после отражения пучок расходится, а продолжения отра-женных лучей сходятся в точке мнимого фокуса F (рис.29). Как и у вогнутого зеркала фокусное расстояние выпуклого зеркала равно f = Rç 2. Поскольку R > 0, то и f – положительное число.

Формула выпуклого зеркала та же, что и для вогнутого зеркала.

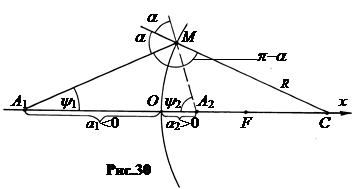Действительно, с учетом правила знаков по теореме синусов для треугольников A ₁ MC и CMA ₂ можно записать (рис.30):

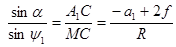, (5.5)

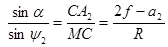, (5.6)

Разделив первое уравнение на второе, получаем:

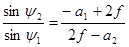. (5.7)

Из условий параксиальности лучей полагаем, что 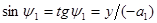, 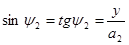. Тогда 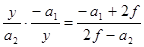. Отсюда 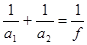. (5.8)

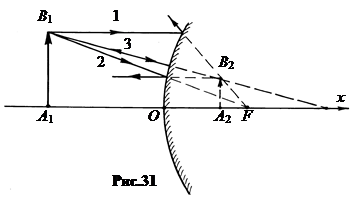При построении изображений в выпуклом зеркале при любом расстоянии от вершины до предмета реализуется только один случай. Изображение получается мнимым, прямым, уменьшенным (рис.31).

8. Плоское зеркало можно рассматривать как частный случай сферического зеркала при R ® ± ∞. В этом случае a ₂ = - a ₁. Изображение мнимое, прямое, натуральной величины.

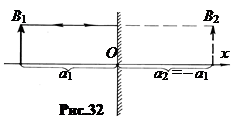Для построения изображения точки предмета достаточно одного луча, нормального зеркалу (рис.32).

Плоское зеркало – единственная оптическая система, дающая полностью не искаженное изображение при любых падающих на него лучах света. Поэтому плоские зеркала широко используются во многих оптических системах.

Date: 2015-08-06; view: 1890; Нарушение авторских прав