Глава 2. Геометрическая оптика

§4. Предмет геометрической оптики (ГО)

1. Предмет ГО. Раздел оптики, в котором изучаются законы распространения света на основе представлений о световых лучах, называется геометрической оптикой.

Физически луч – это направление распространения энергии ЭМ волны в пространстве. Однако в том случае, когда размеры неоднородностей в оптических средах много больше длины волны света l, а протяженность световых лучей такова, что дифракционные явления практически отсутствуют, понятие светового луча абстрагируется к прямой линии.

Таким образом, геометрическая оптика есть предельный случай реальной волновой оптики, соответствующий исчезающе малой длине световой волны по сравнению с размерами препятствий, отверстий, предметов и их изображений.

ГО не рассматривает вопрос о природе света. Ее задача состоит в математическом исследовании хода световых лучей в оптических средах с заданным коэффициентом преломления n. Законы ГО позволяют создать упрощенную, но практически достаточно точную теорию оптических систем. Она объясняет, в основном, образование оптических изображений, дает возможность вычислить аберрации оптических систем и разрабатывать методы их исправления.

Теория геометрической оптики была завершена в середине 17 века установлением принципа Ферма, из которого вытекали все известные к тому времени законы ГО.

2. Законы ГО. Они включают в себя 4 закона. Три первые из них были известны еще Евклиду (3 век до н.э.), а четвертый (закон преломления) был открыт в начале 17 века.

a. 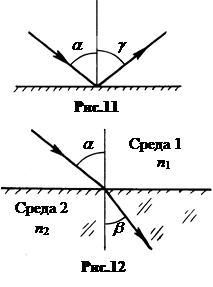Луч света в однородной среде есть прямая линия.

б. Пересекающиеся лучи не возмущают друг друга.

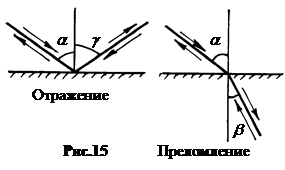
в. Угол отражения равен углу падения, а отраженный луч лежит в одной плоскости с падающим лучом и перпендикуляром, восстановленным в точку падения (закон отражения, рис.11), g = a.

г. Отношение синуса угла падения луча на границе двух прозрачных сред к синусу угла преломления обратно пропорционально отношению абсолютных показателей преломления этих сред. Преломленный луч лежит в одной плоскости с падающим лучом и перпендикуляром, восстановленным в точку падения (закон преломления, Виллеброрд Снель, 1620, Рене Декарт, 1637, рис.12).

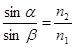. Закон преломления. (4.1)

3. Принцип Ферма. В 1660 году Пьер Ферма сформулировал в виде аксиомы следующий принцип: время распространения светового луча от одной точки пространства к другой должно быть экстремальным из времен, возможных в данных условиях, то есть максимальным, минимальным или стационарным (одинаковым во всех возможных случаях).

Из принципа Ферма вытекают все законы ГО.

a. Прямолинейность распространения света. Свет распространяется в однородной среде по прямой линии, так как это кратчайшее расстояние между двумя точками. Время прохождения светом прямой минимально.

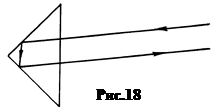
б. Закон отражения. Пусть свет, идущий из точки A, с координатами x ₁, y ₁, отражается от поверхности в произвольной точке O с координатами x, y и попадает в точку B с координатами x ₂, y ₂ (рис.13).

Вопрос: где должна находится точка O, чтобы время прохождения луча из точки A в точку B с однократным отражением от поверхности было экстремальным?

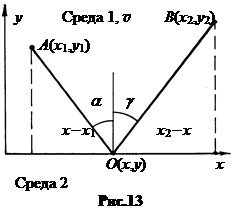Время движения луча от точки A к B есть t = (AO + OB) ½v, где v – скорость света в среде 1. Из условия экстремальности времени следует:

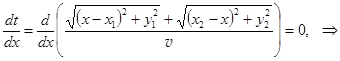
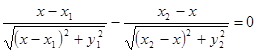. (4.2)

Или, sin a = sin g, a = g. (4.3)

Это закон отражения. Экстремальному, в данном случае минимальному времени t соответствует такое положение точки O, при котором угол отражения g равен углу падения a.

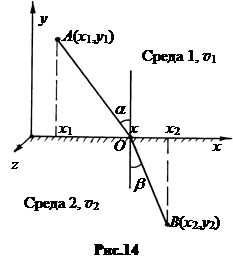в. Закон преломления. Пусть свет проходит из среды 1 в среду 2, пересекая границу раздела сред в точке O с координатами x, y (рис.14). Вопрос: где должна находится точка O, чтобы время прохождения луча от точки A до точки B было экстремальным?

Время распространения света в среде 1 есть t ₁ = AOçv ₁, в среде 2 есть t ₂ = OBçv ₂, где v ₁ и v ₂ – скорость света в соответствующих средах. Из условия экстремальности времени следует:

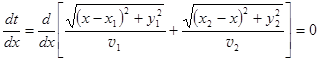. (4.4)

Отсюда ,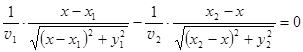

или . (4.5)

Если скорости света в средах v ₁ и v ₂ выразить через скорость света c в вакууме, v ₁ = cçn ₁, v ₂ = cçn ₂, где n ₁ и n ₂ – абсолютные показатели сред, то:

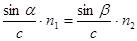, или 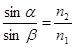. Это закон преломления Декарта-Снелля. (4.6)

Отношение n ₂ çn ₁ = v ₁ çv ₂ = n ₂₁ называют относительным показателем преломления среды 2 к среде 1. Это характеристика границы раздела двух сред. Абсолютные показатели преломления двух сред n ₁ и n ₂ характеризуют преломление света на границе их с вакуумом.

Луч падающий, луч отраженный и луч преломленный лежат в одной плоскости с перпендикуляром, восстановленным в границе раздела в точке падения. Последнее очевидно, поскольку смещение точки O вдоль оси z приводит к удлинению пути, а значит и времени.

4. Обратимость световых лучей. Во всех явлениях отражения и преломления соблюдается закон обратимости световых лучей. Суть его в том, что при изменении направления лучей на обратное их взаимное расположение не меняется (рис.15).

Принцип обратимости сохраняется при каком угодно числе отражений и преломлений, поскольку он соблюдается при каждом из них. Поэтому принцип обратимости справедлив во всех задачах, связанных с построением изображений.

5. Полное отражение света. Когда свет падает на поверхность среды с бόльшим коэффициентом преломления, какая-то его часть всегда проходит в эту более плотную среду. Если же свет падает на поверхность среды с меньшим коэффициентом преломления, то при некоторых углах падения весь свет будет отражаться обратно. Говорят, происходит полное отражение.

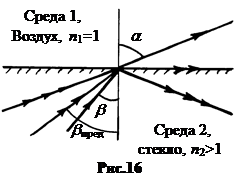Пусть изнутри стеклянного блока падает на его поверхность, граничащую с воздухом, луч света. Угол между нормалью и вышедшим из стекла лучом всегда больше, чем угол b внутри стекла (n ₁ < n ₂). Если увеличивать b, то при каком-то его определенном значении b _пред угол a достигнет 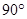(рис.16). При дальнейшем увеличении угла b > b _пред луч будет полностью отражаться обратно в стекло.

Предельный угол полного внутреннего отражения найдется из закона преломления.

. (4.7)

Таблица 4.1
Вещество		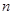b пред,˚
Алмаз	2,417
Вода	1,334
Глицерин	1,474
Лед	1,310
Орг. стекло	1,490
Сероуглерод	1,628
Спирт этиловый	1,361
Стекло разное	1,47 - 2,04	30 - 42
Эфир этиловый	1,354
Янтарь	1,532

В таблице 4.1 приведены значения показателей преломления некоторых веществ и значения предельных углов полного внутреннего отражения. С увеличением показателя преломления n предельный угол b _пред уменьшается.

Полное внутреннее отражение используется в оптических приборах для удлинения оптического пути без увеличения габаритов прибора (бинокли), для переворачивания изображений и так далее. Основным элементом здесь являются призмы полного внутреннего отражения.

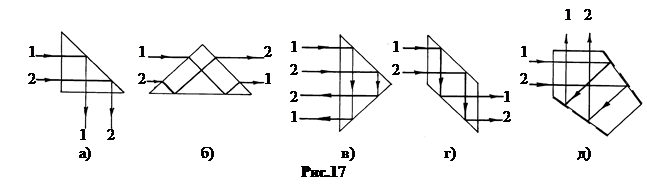На рис.17 показан ход лучей в призмах с одной отражающей гранью (а. Прямоугольная, б. Призма Дове) и ход лучей в призмах с двумя отражающими гранями (в. Прямоугольная, г. Призма – ромб, д. Пентапризма).

Существуют призмы с тремя отражающими гранями, а так же системы призм. Множество одинаково ориентированных трехмерных призм типа «в» с прямым углом при вершине образуют катафоты (рис.18). Это оптические системы, способные в определенных угловых пределах отражать свет так, что отраженный луч выходит параллельно падающему независимо от угла падения света на грань призмы. Катафоты широко используются в автомобильном транспорте, наносятся на дорожные знаки, даже на ранцы и одежду детей.

Полное внутреннее отражение используется в волоконных световодах, представляющий собой оптически прозрачный цилиндр радиуса R ₁, окруженный оболочкой радиуса R ₂. Так как показатель преломления внутреннего цилиндра n ₁ больше показателя преломления оболочки n ₂, то запущенный в торец световой луч идет вдоль волокна, многократно отражаясь от границы раздела диэлектриков (рис.19).

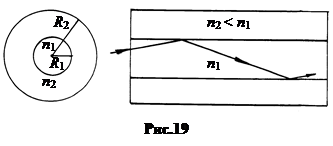В зависимости от назначения диаметр внутреннего волокна световода 2 R ₁ составляет от нескольких микрон до нескольких десятков микрон, а диаметр наружной оболочки – от нескольких десятков до сотен микрон. На основе волоконной оптики разрабатываются системы оптической связи, способные пропускать огромные потоки информации.

6. Преломление луча света, проходящего через призму. Пусть на одну грань призмы падает луч света, а из другой грани он выходит (рис.20). Угол между гранями e. Проходящий через призму луч в результате двукратного преломления на ее гранях отклоняется на угол j к основанию призмы. Угол отклонения j зависит от преломляющего угла призмы e и показателя преломления n вещества призмы.

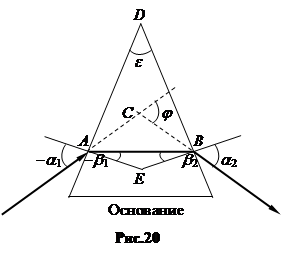Найдем связь между величинами j, e, n. Углы, отсчитываемые от нормали по часовой стрелке, считаем положительными, против часовой стрелки – отрицательными. Из D ACB имеем: j = (-a ₁ + b ₁) + (a ₂ - b ₂) = (a ₂ - a ₁) - (b ₂ - b ₁). Из фигуры ADBE следует, что e = b ₂ - b ₁. Подставив, получаем:

j = -a ₁ + a ₂ - e. (4.8)

Запишем закон преломления луча в точках A и B, полагая, что призма находится в воздухе с показателем преломления 1.

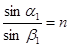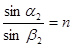, . (4.9)

Выразим отсюда a ₁ и a ₂ и подставим в формулу (4.8). Получаем:

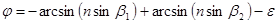. (4.10)

В формулу входят две неизвестные величины b ₁ и b ₂. Можно перейти к одной, подставив b ₂ = b ₁ - e.

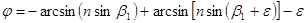. (4.11)

Исследуем j на экстремум, продифференцировав формулу (4.11) по b ₁ и приравняв производную к нулю, . (4.12)

Условие выполняется в двух случаях: b ₁ = b ₁ + e, - b ₁ = b ₁ + e. Первое условие лишено смысла, так как e ¹ 0. Остается второе, из которого следует: - b ₁ = eç 2. Так как e = b ₂ - b ₁, то b ₂ = - b ₁ = eç 2.

Можно показать, что экстремум соответствует минимуму j (вторая производная при - b ₁ = b ₂ положительна). Следовательно, при симметричном ходе луча, когда углы a ₁ и a ₂ одинаковы по модулю, угол отклонения луча 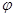минимален.

Подставив b ₁ = - eç 2, b ₂ = eç 2 в формулу (4.10), получаем:

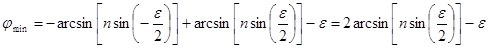. (4.13)

Или 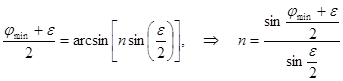. (4.14)

Поскольку показатель преломления вещества призмы n зависит от длины волны l, то прошедший сквозь призму пучок полихроматического света расщепляется в спектр. Поэтому используемые в таком качестве призмы называются спектральными или дисперсионными.

Date: 2015-08-06; view: 861; Нарушение авторских прав