Пример решения задач. Пример.1. Пучок естественного света падает на полированную поверхность стеклянной пластины, погруженной в жидкость

Пример. 1. Пучок естественного света падает на полированную поверхность стеклянной пластины, погруженной в жидкость. Отраженный от пластины пучок света составляет угол j = 97⁰ с падающим пучком (рис.1). Определить показатель преломления n жидкости, если отраженный свет полностью поляризован.

Рис. 1.

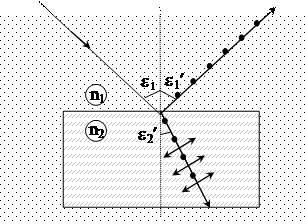Решение. Согласно закону Брюстера, свет, отраженный от диэлектрика, полностью поляризован в том случае, если:

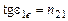tge_1в=n₂₁, (1)

где n₂₁- относительный показатель преломления второй среды (стекла) относительно первой (жидкости).

Относительный показатель преломления равен отношению абсолютных показателей преломления этих сред. Следовательно:

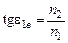tge_1в= n₂/ n₁. (2)

Согласно условию задачи, отраженный луч повернут на угол относительно падающего луча. Так как угол падения равен углу отражения, то:

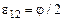e_1в=j/2 (3)

и, следовательно:

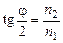tg(j/2)= n₂/ n₁, (4)

откуда:

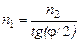n₁= n₂/[ tg(j/2)]. (5)

Cделав подстановку числовых значений, получим

n₁=1,33.

Контрольная работа № 5.

1. На горизонтальном дне бассейна глубиной h=1,5 м. лежит плоское зеркало. Луч света входит в воду под углом i₁=45⁰. Определить расстояние s от места вхождения луча в воду до места выхода его на поверхность воды после отражения от зеркала. Показатель преломления воды n=1,33.

2. Луч света падает на плоскую границу раздела двух сред, частично отражается и частично преломляется. Определить угол падения, при котором отраженный луч перпендикулярен преломленному лучу.

3. На плоскопараллельную стеклянную (n=1,5) пластинку толщиной d=5 см падает под углом i=30⁰ луч света. Определить величину бокового смещения луча, прошедшего сквозь эту пластинку.

4. Человек с лодки рассматривает предмет, лежащий на дне водоёма (n=1,33). Определить его глубину, если при определении «на глаз» по вертикальному направлению глубина водоёма кажется равной 1,5 м.

5. Человек с лодки рассматривает предмет, лежащий на дне. Глубина водоёма везде одинакова и равна H. Определить зависимость кажущейся глубины h предмета от угла i, образуемого лучом зрения с нормалью к поверхности воды.

6. Предельный угол полного отражения на границе стекло-жидкость i_пр=65⁰. Определить показатель преломления жидкости, если показатель преломления стекла n=1,5.

7. Луч света выходит из стекла в вакуум. Предельный угол полного отражения i_пр=42⁰. Определить скорость света в стекле.

8. На дне сосуда, наполненного водой (n=1,33) до высоты h=25 см, находится точечный источник света. На поверхности плавает непрозрачная пластинка так, что центр пластинки находится над источником света. Определить минимальный диаметр пластинки, при котором свет не пройдет через поверхность воды.

9. Длинное тонкое волокно, выполненное из прозрачного материала с показателем преломления n=1,35, образует световод. Определить максимальный угол к оси световода, под которым световой луч ещё может падать на торец, чтобы пройти световод без ослабления.

10. Определит на какой угол j отклоняется световой луч от своего первоначального направления при переходе из воздуха в воду, если угол падения i=75⁰.

11. Расстояние а от светящейся точки S до вогнутого сферического зеркала равно двум радиусам кривизны. Определить положение изображения точки и построить это изображение.

12. На рисунке показаны положения главной оптической оси MN сферического зеркала, светящейся точки S и её изображения S*. Определить построением положение центра сферического зеркала и его фокуса. Указать вид использованного зеркала.

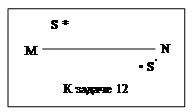
13. На рисунке показаны положения главной оптической оси MN сферического зеркала, светящейся точки S и её изображения S ^′. Определить построением положение центра сферического зеркала и его фокуса. Указать вид использованного зеркала.

14. Вогнутое сферическое зеркало даёт действительное изображение, которое в три раза больше предмета. Определить фокусное расстояние зеркала, если расстояние между предметом и изображением равно 20 см.

15. Выпуклое сферическое зеркало имеет радиус кривизны 60 см. На расстоянии 10 см от зеркала поставлен предмет высотой 2 см. Определить: 1) положение изображения; 2) высоту изображения, построить чертёж.

16. Построить изображение произвольной точки S, которая лежит на главной оптической оси собирающей линзы.

17. Построить изображение произвольной точки S, которая лежит на главной оптической оси рассеивающей линзы.

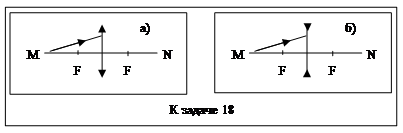
18. Определить построением ход луча после преломления его собирающей (рис. а)) и рассеивающей (рис. б)) линзами. На рисунках MN – положение главной оптической оси; F – фокусы линзы. Среды по обе стороны линзы одинаковы.

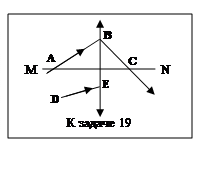
19. На рисунке показаны положения оптической оси MN тонкой собирающей линзы и ход одного луча АВС через эту линзу. Построить ход луча DE. Среды по обе стороны линзы одинаковы.

20. На рисунке показаны положения оптической оси MN тонкой рассеивающей линзы, ход луча 1, падающего на линзу и преломленного луча 2. Определить построением оптический центр и фокусное расстояние линзы. Среды по обе стороны линзы одинаковы.

21. Фокусное расстояние линзы, находящейся в воздухе, равно 5 см. Фокусное расстояние той же линзы, погруженной в некоторую жидкость, равно 35 см. Определить показатель преломления жидкости, если показатель преломления стекла 1,5.

22. Чему равен показатель преломления стекла, если при отражении от него света отраженный луч будет полностью поляризован при угле преломления 30^о?

23. Показать, что луч света, последовательно отразившийся от двух взаимно перпендикулярных плоских зеркал, изменит свое направление на противоположное.

24. На столе лежит лист бумаги. Луч света, падающий на бумагу под углом 30^о, дает на ней светлое пятно. На сколько сместится это пятно, если на бумагу положить плоскопараллельную стеклянную пластинку толщиной 5 см? (n = 1,5).

25. Луч падает под углом 60^о на стеклянную пластинку толщиной 30 мм. Определить боковое смещение луча после выхода из пластины.

26. Луч света проходит из среды с показателем преломления n₁ в среду с показателем преломления n₂ . Показать, что если угол между отраженным и преломленным лучами равен p/2, то выполняется условие tg e₁ = n₂ /n₁. (e₁ - угол падения).

27. Двояковыпуклая линза имеет одинаковые радиусы кривизны поверхности. При каком радиусе кривизны поверхностей линзы главное фокусное расстояние будет равно 20 см?

28. Линза с фокусным расстоянием 16 см дает резкое изображение предмета при двух положениях, расстояние между которыми 60 см. Найти расстояние от предмета до экрана.

29. Из стекла требуется изготовить плосковыпуклую линзу, оптическая сила которой равна 5 дптр. Определить радиус кривизны выпуклой поверхности линзы.

30. Определить радиус кривизны выпуклой поверхности линзы, если при отношении радиусов кривизны поверхностей линзы, равном 3, ее оптическая сила равна 8 дптр.

31. Расстояние между двумя щелями в опыте Юнга равно 1 мм, расстояние от щелей до экрана равно 3 м. Определить длину волны, испускаемой источником монохроматического света, если ширина полос интерференции на экране равна 1,5 мм.

32. На мыльную пленку (n = 1,3), находящуюся в воздухе, падает нормально пучок белого света. При какой наименьшей толщине пленки отраженный свет с длиной волны 0,55 мкм окажется максимально усиленным в результате интерференции?

33. Расстояние между пятым и двадцать пятым светлыми кольцами Ньютона равно 9 мм. Радиус кривизны линзы 15 м. Найти длину волны монохроматического света, падающего нормально на установку. Наблюдение проводится в отраженном свете.

34. Установка для получения колец Ньютона освещается светом от ртутной дуги, падающим нормально. Наблюдение производится в проходящем свете. Какое по порядку светлое кольцо, соответствующее линии 579,1 нм, совпадает со следующим светлым кольцом, соответствующим линии 577 нм?

35. Диаметры двух светлых колец Ньютона соответственно равны 4,0 и 4,8 мм. Порядковые номера колец не определялись, но известно, что между двумя измеренными кольцами расположено три светлых кольца. Кольца наблюдаются в отраженном свете (l = 500 нм). Найти радиус кривизны плосковыпуклой линзы, взятой для опыта.

36. На экране наблюдается интерференционная картина от двух когерентных источников света с длиной волны 480 нм. Когда на пути одного из пучков поместили тонкую пластинку из плавленого кварца с показателем преломления 1,46, то интерференционная картина сместилась на 69 полос. Определить толщину кварцевой пластинки.

37. Плоская световая волна (l = 0,5 мкм) падает нормально на диафрагму с круглым отверстием диаметром 1 см. На каком расстоянии от отверстия должна находиться точка наблюдения, чтобы отверстие открывало: 1) одну зону Френеля; 2) две зоны Френеля.

38. На мыльную пленку падает под углом 30^о параллельный пучок белых лучей. В отраженном свете пленка кажется красной (l = 700 нм). Какова наименьшая возможная толщина пленки?

39. На щель падает нормально параллельный пучок монохроматического света с длиной волны l. Ширина щели равна 6 l. Под каким углом будет наблюдаться третий дифракционный минимум света?

40. На дифракционную решетку нормально падает пучок света от разрядной трубки, наполненной гелием. На какую линию в спектре третьего порядка накладывается красная линия гелия (l = 6,7×10^-7м) спектра второго порядка?

41. Тонкая металлическая пластинка имеет круглое отверстие диаметром 4 мм. На пластинку падает нормально параллельный пучок лучей (l = 500 нм). На экране, удаленном на 1 м от пластинки, наблюдается дифракционная картина. Темное или светлое пятно находится в центре дифракционной картины?

42. Дифракционная решетка содержит 500 штрихов на 1 мм. На решетку падает нормально монохроматический свет (l = 600 нм). На какой угол от нормали к решетке нужно отклонить трубу спектрометра, чтобы навести её на спектральную линию третьего порядка? Четвертого порядка?

43. Постоянная кристаллической решетки каменной соли равна 28 нм. Определить длину волны рентгеновских лучей, падающих на кристалл, если дифракционный максимум первого порядка наблюдается, когда лучи падают под углом 17^о к поверхности кристалла.

44. На пластинку со щелью, ширина которой 0,05 мм, падает нормально монохроматический свет с длиной волны 0,7 мкм. Определить угол отклонения лучей, соответствующий первому дифракционному максимуму.

45. Дифракционная решетка, освещенная нормально падающим монохроматическим светом, отклоняет спектр третьего порядка на угол 30^о. На какой угол отклоняет она спектр четвертого порядка?

46. Дифракционная решетка содержит 200 штрихов на 1 мм. На решетку падает нормально монохроматический свет (l = 0,6 мкм). Максимум какого наибольшего порядка дает эта решетка?

47. На дифракционную решетку, содержащую 400 штрихов на 1 мм, падает нормально монохроматический свет (l = 0,6 мкм). Найти общее число дифракционных максимумов, которые дает эта решетка. Определить угол дифракции, соответствующий последнему максимуму.

48. В опыте Юнга по дифракции расстояние между щелями d=0,07мм, а расстояние L от двойной щели до экрана равно 2 м. При освещении зелёным светом расстояние между соседними светлыми дифракционными полосами оказалось равным Δx=16 мм. Определите по этим данным длину волны.

49. На дифракционную решетку, имеющую период =1,2·10^-3см, нормально падает монохроматическая волна. Оценить длину волны, если угол между спектрами второго и третьего порядка Δφ =2⁰30'.

50. Определить длину отрезка L₁, на котором укладывается столько же длин волн монохроматического света в вакууме, сколько их укладывается на отрезке L₂=5 мм в стекле. Показатель преломления стекла n₂=1,5.

51. В опыте Юнга расстояние между щелями d=1мм, а расстояние L от щелей до экрана равно 3 м. Определить: 1) положение первой светлой полосы; 2) положение третьей темной полосы, если щели освещать монохроматическим светом с длиной волны λ=0,5 мкм.

52. В опыте с зеркалами Френеля расстояние d между мнимыми изображениями источника света равно 0,5 мм, расстояние L от них до экрана равно 5 м. В желтом свете ширина интерференционных полос равна 6 мм. Определить длину волны желтого света.

53. Расстояние между двумя щелями в опыте Юнга равно d=0,5 мм (λ=0,6 мкм). Определить расстояние L от щелей до экрана, если ширина интерференционных полос равна 1,2 мм.

54. В опыте Юнга расстояние L от щелей до экрана равно 3 м. Определить угловое расстояние между соседними светлыми полосами, если третья светлая полоса на экране отстоит от центра интерференционной картины на расстоянии 4,5 мм.

55. Если в опыте Юнга на пути одного из интерферирующих лучей поместить перпендикулярно этому лучу тонкую стеклянную пластинку (n=1,5), то центральная светлая полоса смещается в положение, первоначально занимаемое пятой светлой полосой. Длина волны λ=0,5 мкм. Определить толщину пластинки.

56. Определить, во сколько раз изменится ширина интерференционных полос на экране в опыте с зеркалами Френеля, если фиолетовый светофильтр (0,4мкм) заменить красным (0,7 мкм).

57. Расстояние от бипризмы Френеля до узкой щели и экрана соответственно равны а=30 см и в=1,5 м. Бипризма стеклянная (n=1,5) с преломляющим углом θ=20^'. Определить длину волны света, если ширина интерференционных полос Δx =0,65 мм.

58. Расстояние от бипризмы Френеля до узкой щели и экрана соответственно равны а=48 см и в=6 м. Бипризма стеклянная (n=1,5) с преломляющим углом θ=10^'. Определить максимальное число полос, наблюдаемых на экране, если λ=600нм.

59. На плоскопараллельную плёнку с показателем преломления n=1,33 под углом i=45⁰ падает параллельный пучок белого света. Определить при какой наименьшей толщине пленки зеркально отраженный свет наиболее сильно окрасится в жёлтый цвет (λ=0,6 мкм).

60. Точечный источник света (λ=0,5 мкм) расположен на расстоянии а=1м перед диафрагмой с круглым отверстием диаметра d=2 мм. Определить расстояние b от диафрагмы до точки наблюдения, если отверстие открывает три зоны Френеля.

61. Определить радиус третьей зоны Френеля, если расстояния от точечного источника света (λ=0,6 мкм) до волновой поверхности и от волновой поверхности до точки наблюдения равны 1,5 м.

62. На диафрагму с круглым отверстием диаметром d=5 мм падает нормально параллельный пучок света с длиной волны λ=0,6 мкм. Определить расстояние от точки наблюдения до отверстия, если отверстие открывает: 1) две зоны Френеля; 2) три зоны Френеля.

63. Определить радиус третьей зоны Френеля для случая плоской волны. Расстояние от волновой поверхности до точки наблюдения равно 1,5 м. Длина волны λ=0,6 мкм.

64. Определить радиус четвертой зоны Френеля, если радиус второй зоны Френеля для плоского волнового фронта равен 2 мм.

65. Определить радиус первой зоны Френеля, если расстояния от точечного источника света (λ=0,5 мкм) до зонной пластинки и от пластинки до места наблюдения a=b=1м.

66. На зонную пластинку падает плоская монохроматическая волна (λ=0,5 мкм). Определить радиус первой зоны Френеля, если расстояние от зонной пластинки до места наблюдения b=1м.

67. Зонная пластинка дает изображение источника, удалённого от неё на 2 м, на расстоянии 1 м от своей поверхности. Где получится изображение источника, если его удалить в бесконечность?

68. Дифракция наблюдается на расстоянии 1 м от точечного источника монохроматического света (λ=0,5 мкм). Посередине между источником света и экраном находится диафрагма с круглым отверстием. Определить радиус отверстия, при котором центр дифракционных колец на экране является наиболее тёмным.

69. На экран с круглым отверстием радиусом =1,2 мм нормально падает параллельный пучок монохроматического света с диной волны λ=0,6 мкм. Определить максимальное расстояние от отверстия на его оси, где ещё можно наблюдать наиболее тёмное пятно.

70. Угол максимальной поляризации при отражении света от поверхности алмаза равен 67,5^о. Определить скорость света в алмазе.

71. В начальном положении плоскости колебаний поляризатора и анализатора совпадают. На какой угол следует повернуть анализатор, чтобы в три раза уменьшить интенсивность света, приходящего к нему от поляризатора?

72. Угол поворота плоскости поляризации желтого света при прохождении через трубку с раствором сахара равен 20^о. Длина трубки 12 см. Определить концентрацию сахара в растворе, если удельное вращение сахара равно 66,5^о на 1 дм при концентрации 1 г/см³.

73. Пластинку кварца толщиной 2 мм, вырезанную перпендикулярно оптической оси, поместили между параллельными николями, в результате чего плоскость поляризации света повернулась на угол 53^о. Определить толщину пластинки, при которой данный монохроматический свет не проходит через анализатор.

74. Коэффициент поглощения красного света (l = 0,77 мкм) в воде равен 2,4×10^-3 мм^-1. Какой толщины слой воды должен пройти параллельный пучок красных лучей, чтобы интенсивность света уменьшилась в два раза?

75. Луч света переходит из глицерина в стекло так, что луч, отраженный от границы раздела этих сред, оказывается максимально поляризованным. Определить угол между падающим и преломленным лучами.

76. Угол между главными плоскостями поляризатора и анализатора составляет 30⁰. Определить изменение интенсивности прошедшего через них света, если угол между главными плоскостями равен 45⁰.

77. Интенсивность естественного света, прошедшего через два николя, уменьшилась в 8 раз. Пренебрегая поглощением света, определить угол между главным плоскостями николей.

78. Определить во сколько раз ослабится интенсивность света, прошедшего через два николя, расположенные так, что угол между их главными плоскостями α=60⁰, а в каждом из николей теряется 8% интенсивности падающего света.

79. Определить во сколько раз ослабится интенсивность света, прошедшего через два николя, расположенные так, что угол между их главными плоскостями α=60⁰, если каждый из николей как поглощает, так и отражает 5% падающего на них света.

80. Определить толщину кварцевой пластинки, для которой угол поворота плоскости поляризации монохроматического света определённой длины волны φ=180⁰. Удельное вращение в кварце для данной длины волны α=0,52 рад/мм.

81. Пластинка кварца толщиной d₁=2 мм, вырезанная перпендикулярно оптической оси кристалла, поворачивает плоскость поляризации монохроматического света определённой длины волны на угол φ₁=30⁰. Определить толщину кварцевой пластинки d₂, помещённой между параллельными николями, чтобы данный монохроматический свет гасился полностью.

82. Определить массовую концентрацию С сахарного раствора, если при прохождении света через трубку длиной L=20 см с этим раствором плоскость поляризации света поворачивается на угол φ=10⁰. Удельное вращение сахара [α] равно 1.17·10^-2 рад·м²/кг.

83. Раствор глюкозы с массовой концентрацией С₁=0,21 г/см³, находящийся в стеклянной трубке, поворачивает плоскость поляризации монохроматического света, проходящего через раствор, на угол φ₁=24⁰. Определить массовую концентрацию С₂ глюкозы в другом растворе в трубке той же длины, если он поворачивает плоскость поляризации на угол φ₂=18⁰.

84. Частица движется со скоростью, равной 0,6 скорости света. Найти отношение кинетической энергии частицы к ее массе покоя.

85. При какой скорости (в долях скорости света и в км/с) кинетическая энергия частицы равна ее энергии покоя.

86. Электрон движется со скоростью, равной 0,8 скорости света. Определить кинетическую энергию электрона: 1) по классической формуле; 2) по релятивистской. Сравнить результаты.

87. Электрон прошел ускоряющую разность потенциалов 10⁶ В. Определить скорость электрона: 1) по классической формуле; 2) по релятивистской. Сравнить результаты.

88. На сколько процентов увеличится суммарная мощность излучения абсолютно черного тела, если температура тела увеличится на 1%?

89. Максимум энергии в спектре абсолютно черного тела приходится на длину волны 2×10^-6 м. На какую длину волны он сместится, если температура тела увеличится на 250 К?

90. Температура абсолютно черного тела равна 2000 К. Определить: 1) длину волны, на которую приходится максимум испускательной способности абсолютно черного тела; 2) максимальную испускательную способность; 3) суммарную мощность излучения.

91. Определить максимальную испускательную способность абсолютно черного тела при температуре 2000 К и мощность, излучаемую с 1 см² волнами, заключенными в узкой полосе спектра от 0,9 до 1,1 l_max.

92. Красная граница фотоэффекта для рубидия равна 810 нм. Определить работу выхода электрона из этого металла.

93. Работа выхода электронов из меди равна 4,5 эВ. Будет ли иметь место фотоэффект, если на медь направить ультрафиолетовые лучи с длиной волны в 300 нм?

94. Какова максимальная скорость фотоэлектронов, вылетающих из цинка при освещении его лучами с длиной волны 230 нм, если работа выхода равна 4 эВ?

95. Какая доля энергии фотона расходуется на работу вырывания электрона, если красная граница фотоэффекта 307 нм и кинетическая энергия электрона 1 эВ?

96. На слой калия в фотоэлементе падает свет с длиной волны 400 нм. Какую наименьшую задерживающую разность потенциалов нужно приложить к фотоэлементу, чтобы фототок прекратился, если работа выхода электрона из калия равна 2 эВ?

97. Мощность солнечного излучения, падающего на площадку в 1 см², расположенную на границе земной атмосферы перпендикулярно лучам Солнца, равна 0,14 Вт. Вычислить световое давление на эту площадку, если она полностью поглощает все лучи.

98. Монохроматический свет (l = 0,6 мкм) падает нормально на зеркальную поверхность. Сколько фотонов падает в 1 с на 1 см², если световое давление равно 5,5×10^-11Н/см²?

99. Фотон энергией 1МэВ испытал соударение со свободным электроном и рассеялся под углом 180^о. Определить энергию фотона, образовавшегося в результате рассеяния, и кинетическую энергию, полученную электроном.

100. При соударении со свободным электроном фотон (l = 10^-10 м) испытал комптоновское рассеяние под углом 60^о. Сколько процентов своей энергии фотон передал электрону?

Физика атома и ядра.

Date: 2015-08-06; view: 6513; Нарушение авторских прав