Золотое сечение в природе

Связь золотого сечения с красотой – вопрос не только человеческого восприятия. Похоже, сама природа выделила Ф особую роль.

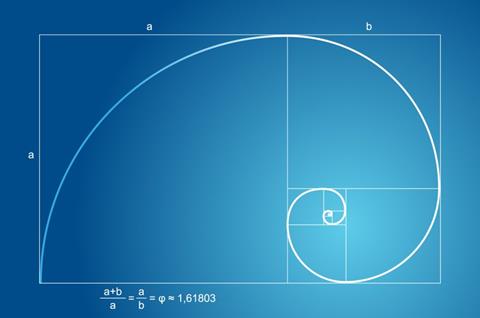
Если взять рассмотренный ранее «размноженный» золотой прямоугольник и провести дугу по диагоналям всех вновь добавленных квадратов, то станет очевидно, что радиус каждой дуги равен длине стороны соответствующего квадрата, а в итоге получится логарифмическая спираль. Эта линия часто встречается в физическом мире: от раковины наутилуса до рукавов галактик.

Форма раковин поражает своим совершенством. Идея спирали в раковинах выражена в совершенной геометрической форме. У большинства улиток, которые обладают раковинами, раковина растет в форме логарифмической спирали, которая точно соответствуют «золотой пропорции».

Такую же спираль можно наблюдать в лепестках распустившейся розы.

Связи между золотым сечением и числами Фибоначчи многочисленны и неожиданны. Это невероятная связь между абстрактным царством чисел и физической реальностью. Например, в ящерице с первого взгляда улавливаются приятные для нашего глаза пропорции – длина ее хвоста так относится к длине остального тела, как 62 к 38.
Если приглядеться к цикорию, то заметно, что от основного стебля образовался отросток. Тут же расположился первый листок. Отросток делает сильный выброс в пространство, останавливается, выпускает листок, но уже короче первого, снова делает выброс в пространство, но уже меньшей силы, выпускает листок еще меньшего размера и снова выброс. Если первый выброс принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции.

Бивни слонов и вымерших мамонтов, когти львов и клювы попугаев являют собой логарифмические формы и напоминают форму оси, склонной обратиться в спираль.

Спиралевидную форму можно увидеть и в шишках сосны, в ананасах, кактусах и т.д.

В живой природе широко распространены формы, основанные на «пентагональной» симметрии (морские звезды, морские ежи, цветы).

Молекула ДНК состоит из двух вертикально переплетенных между собой спиралей. Длина каждой из этих спиралей составляет 34 ангстрема, ширина 21 ангстрема. (1 ангстрем — одна стомиллионная доля сантиметра). 21 и 34 — это цифры, следующие друг за другом в последовательности чисел Фибоначчи, то есть соотношение длины и ширины логарифмической спирали молекулы ДНК несет в себе формулу золотого сечения 1:1,618.

Форма стрекозы тоже соответствует законам золотой пропорции: отношение длин хвоста и корпуса равно отношению общей длины к длине хвоста.

Золотое сечение присутствует в строении всех кристаллов, но большинство кристаллов микроскопически малы, так что мы не можем разглядеть их невооруженным глазом. Однако снежинки (водные кристаллы), вполне доступны нашему взору.

Все изысканной красоты фигуры, которые образуют снежинки, все оси, окружности и геометрические фигуры в снежинках также всегда без исключений построены по совершенной четкой формуле золотого сечения.

У подсолнуха семена расположены по спиралям двух видов: по часовой и против часовой стрелки. По часовой стрелки - 21 спираль, против часовой – 34. Это пара соседних чисел из ряда Фибоначчи.

По-настоящему сложный вопрос – откуда растения «знают», что их листья/семена должны расти в соответствии с последовательностью Фибоначчи?
Стебли растений имеют коническую форму, и листья на них растут радиально, если смотреть сверху. Французский кристаллограф Огюст Браве заметил, что каждый следующий лист повёрнут на 137,5º от предыдущего. Посчитаем 360º 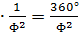, и получим угол в 137,5º, который иногда называют «золотым» углом.

Ботаники утверждают, что дроби, характеризующие винтовые оси растений, образуют строгую математическую последовательность, состоящую из отношений соседних чисел Фибоначчи, то есть:
1/2, 1/3, 2/5, 3/8, 5/13, 8/21, 13/34,…
Какова же „физическая“ причина, лежащая в основе этих законов?
Ответ очень прост: именно при таком расположении листьев достигается максимум притока солнечной энергии к растению. В биологическом и растительном мире вступает в действие принцип экономии материи, который не действует в неорганическом мире.

Date: 2015-07-27; view: 18919; Нарушение авторских прав