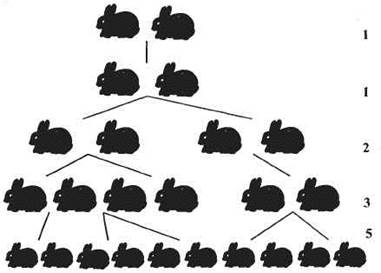
Задача о размножении кроликов

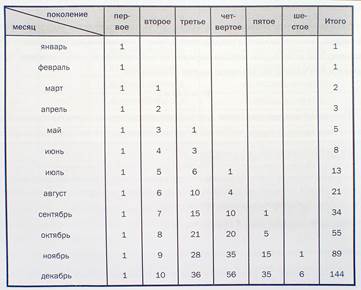Сколько пар кроликов будет у нас через год, если в январе у нас была одна пара, которая каждый месяц производит на свет другую пару, начиная с марта, а каждая новая пара, в свою очередь, производит собственное потомство, начиная со второго месяца своего существования?

Фибоначчи составил таблицу, в графе «Итого» подсчитывая число пар в конце каждого месяца. Беглый взгляд на эту таблицу показывает странную закономерность в последовательности: каждое число является суммой двух предыдущих.

В конце 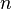-го месяца количество пар кроликов будет равно количеству пар в предыдущем месяце плюс количество новорожденных пар, которых будет столько же, сколько пар было два месяца назад. Таким образом:

Ряд чисел 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 и т. д. известен как ряд Фибоначчи. Каждое число, начиная с третьего, равно сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 = 13; 8 + 13 = 21; 13 + 21 = 34 и т. д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21: 34 = 0,617, а 34: 55 = 0, 618. Это отношение обозначается символом Ф. Только это отношение – 0, 618: 0, 382 –дает непрерывное деление отрезка прямой в золотой пропорции. Он может увеличиваться или уменьшаться до бесконечности, а меньший отрезок всегда будет так относиться к большему, как больший ко всему.

Формула общего члена последовательности была обнаружена в 1843 г. Французским математиком Жаком Бине:

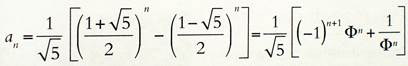
Она показывает, что предел отношений соседних членов последовательности Фибоначчи равен золотому сечению.

Date: 2015-07-27; view: 2453; Нарушение авторских прав