Вычисление и построение ускорения Кориолиса

Для определения величины и направления кориолисова ускорения прежде всего следует вычислить и направить относительную скорость . Далее строится вектор переносной угловой скорости и переносится параллельно себе в точку М. После этого остается воспользоваться правилом векторной алгебры для определения векторного произведения.

Ускорение 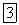направлено перпендикулярно плоскости, в которой лежат векторы и 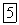, в ту сторону, из которой кратчайший поворот от вектора к вектору виден происходящим против часовой стрелки (рис. 114).

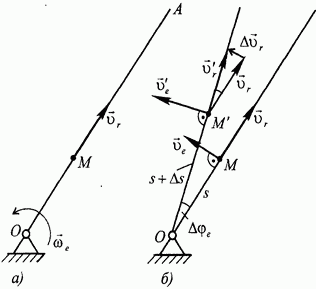
Рис. 113.

Модуль ускорения Кориолиса определяется по формуле

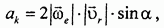
где - угол между векторами и .

Ускорение Кориолиса равно нулю в следующих случаях.

1. Когда один из векторных сомножителей равен нулю ( или ).

2. Когда векторы и коллинеарны. В этом случае угол равен либо 0 (рис. 115, а), либо 180° (рис. 115,5), поэтому , а вместе с ним и , равны нулю.

3. Когда переносное движение является поступательным. В этом случае движение подвижных осей не имеет вращательной составляющей, поэтому переносная угловая скорость равна нулю в любой момент времени: . В любой момент времени будет равно нулю и кориолисово ускорение, и теорема сложения ускорений при поступательном переносном движении принимает такой же вид, как и теорема сложения скоростей:

Так обстоит дело, например, при сложном движении точки М, показанном на рис. 116. Переносным движениемявляется движение стержня АВ (спарника), которое при условии является поступательным. УскорениеКориолиса в данном случае отсутствует.

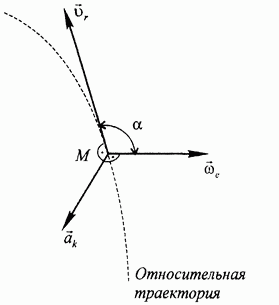
Рис. 114

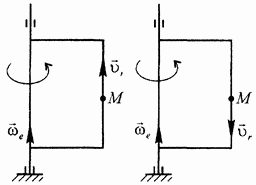
Рис. 115

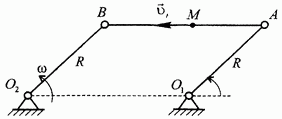
Рис. 116.

Пример.

Жесткая рамка в виде прямоугольного треугольника ОАВ вращается вокруг неподвижной оси сугловой скоростью (рис. 117). По гипотенузе ОВ движется точка М согласно уравнению . Найти абсолютную скорость и абсолютное ускорение точки момент времени .

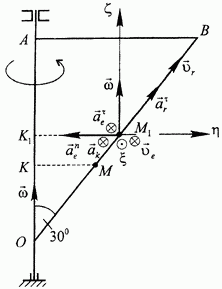
Рис. 117.

Точка М совершает сложное движение- одновременно движется относительно рамки (подвижная система координат) и окружающих неподвижных предметов (неподвижная система координат). Переносным движениемявляется вращательное движение рамки, относительным - прямолинейное движение точки М вдоль прямой ОВ. Пусть М - положение точки в текущий момент в расчетный момент .

Переносная скорость точки М найдется как линейная скорость точки М рамки, совпадающей в данный момент с движущейся точкой М. (При определении переносной скорости можно пользоваться следующим приемом: мысленно остановить относительное движение и найти скорость в оставшемся движении). Так как рамка вращается, переносную скорость вычисляем по формуле

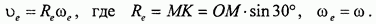
Подставляя данные из условия задачи, находим:

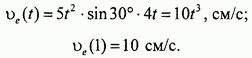
Примем, что в расчетный момент плоскость рамки совпадает с плоскостью рисунка. Тогда вектор будет направлен перпендикулярно к плоскости рисунка "от нас".

Величину относительной скорости находим, дифференцируя закон относительного движения

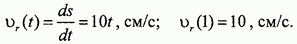
Вектор направлен вдоль прямой ОВ в сторону движения (к точке В).

Складывая векторы и , известные теперь по величине и направлению, находим абсолютную скорость точки М.

Так как слагаемые векторы взаимно перпендикулярны, модуль абсолютной скорости вычисляем потеореме Пифагора:

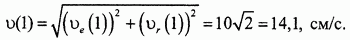
Абсолютное ускорение находим по теореме сложения ускорений:

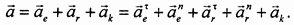
Дальнейшее решение состоит в вычислении и построении каждого из составляющих ускорений и последующем их суммировании.

Для определения переносного касательного ускорения сначала вычисляем переносное угловое ускорение

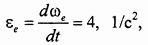
а далее и само ускорение:

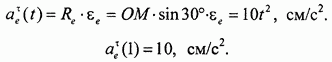
Направление вектора совпадает с направлением вектора ("от нас").

Вычисляем переносное нормальное ускорение:

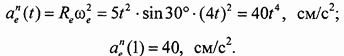
Направлено по радиусу переносного вращения к оси вращения (к точке ).

Относительное касательное ускорение равно

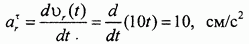
и направлено в одну сторону с относительной скоростью . Так как относительное движение прямолинейное, относительное нормальное ускорение равно нулю .

Условно переносим вектор переносной угловой скорости в точку М и определяем модуль ускоренияКориолиса:

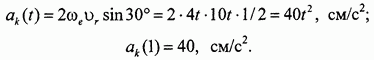
Вектор направлен перпендикулярно плоскости рисунка "от нас".

Выбираем с началом в точке М вспомогательные оси , и вычисляем методом проекций абсолютноеускорение в расчетный момент :

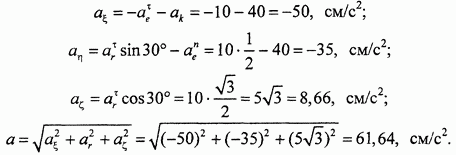
Date: 2015-07-27; view: 653; Нарушение авторских прав