Теорема сложения ускорений

Предварительно получим общие выражения для относительного и переносного ускорений.

Относительное ускорение характеризует скорость изменения относительной скорости по отношению к подвижной системе координат. Следовательно, оно выражается локальной производной по времени от относительной скорости точки:

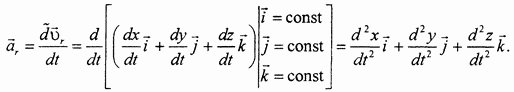
Переносное ускорение, в соответствии с его определением и смыслом, выразится так:

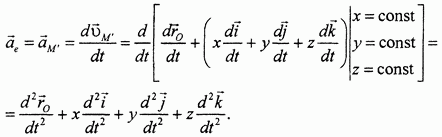
Абсолютное ускорение точки характеризует скорость изменения абсолютной скорости по отношению к неподвижным осям и поэтому будет равно

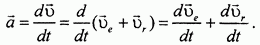
Производные вычисляются по отношению к неподвижным осям, поэтому при дифференцировании выражений для и будут переменными как координаты х, у, z, так и орты 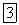. Выполнив дифференцирование, с учетом полученных выше выражений для переносного и относительного ускорений можем записать:

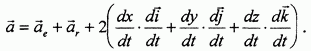
Видно, что абсолютное ускорение складывается из переносного и относительного ускорений и из дополнительного слагаемого, которое получило название ускорения Кориолиса (кориолисова ускорения). После некоторых преобразований, которые здесь не приводятся, ускорение Кориолиса представляется в виде следующего выражения:

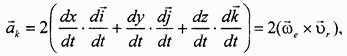
где - вектор переносной угловой скорости, 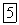- вектор относительной линейной скорости точки.

Таким образом, приходим к теореме сложения ускорений, которую можно записать в виде следующих двух векторных равенств:

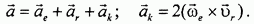
Словесная формулировка теоремы такова: абсолютное ускорение при сложном движении точки равно геометрической сумме ее относительного, переносного и кориолисова ускорений. Ускорение Кориолиса равно удвоенному векторному произведению вектора переносной угловой скорости на вектор относительной линейной скорости точки.

Date: 2015-07-27; view: 353; Нарушение авторских прав