Теорема сложения скоростей

Вначале получим общие выражения для абсолютной, относительной и переносной скоростей, основываясь на введенных выше определениях и результатах кинематики точки, изложенных в лекции 7. Однако предварительно сделаем одной замечание.

Один и тот же переменный вектор (радиус-вектор, вектор скорости и т.д.) в различных системах координат, движущихся относительно друг друга, изменяется по-разному. Соответственно, отличными друг от друга будут и его производные, вычисленные по отношению к разным системам координат. Поэтому в кинематике всегда следует отдавать себе отчет в том, относительно какой системы координат вычисляется та или иная векторнаяпроизводная.

Пусть - радиусы-векторы точки М, проведенные из начала неподвижной и подвижной систем координат соответственно, - радиус-вектор подвижного начала относительно неподвижного (рис. 112).

Абсолютная скорость точки М, в соответствии с определением, будет выражаться производной по времени от радиуса-вектора , вычисленной относительно неподвижной системы координат:

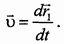
Относительная скорость выражается производной от радиуса-вектора , вычисленной относительно подвижной системы координат. Вводя для производных относительно подвижной системы координат знак - (тильда), запишем:

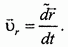
При вычислении производной относительно подвижной системы координат (ее называют также относительной производной, локальной производной) движение подвижных осей игнорируется - оси считаются как бы неподвижными (остановленными).

Пусть х, у, z — текущие координаты точки М в подвижных осях, - орты этих осей. Тогда, учитывая сказанное о вычислении локальной производной, для относительной скорости получим:

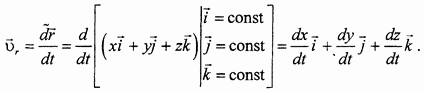
Переносная скорость точки M, в соответствии с определением, выражается производной от радиуса-вектора точки подвижной системы координат, вычисленной относительно неподвижной системы координат:

Здесь учтено, что вектор ОМ имеет в подвижном координатном базисе то же представление, что и вектор , только координаты х, у, z являются для него постоянными (так как точка М неизменно связана с подвижной системой координат).

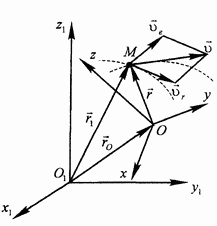
Рис. 112.

Найдем теперь зависимость между абсолютной, относительной и переносной скоростями. Для этого продифференцируем относительно неподвижной системы координат обе части равенства

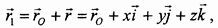
учитывая, что по отношению к неподвижной системе все величины в нем являются переменными: , а также - от движения подвижных осей, - вследствие относительного движения. Будем иметь:

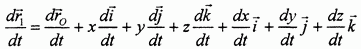
или, используя введенные выше обозначения:

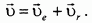
Мы получили, что абсолютная скорость точки при ее сложном движении равна геометрической сумме переносной и относительной скоростей.

В этом и состоит теорема сложения скоростей при сложном движении точки. Геометрически это означает, что абсолютная скорость выражается направленной диагональю параллелограмма, сторонами которого служат векторы относительной и переносной скоростей (см. рис. 122; штриховыми линиями на рисунке показаны абсолютная и относительная траектории точки).

Date: 2015-07-27; view: 481; Нарушение авторских прав