Условия (уравнения) равновесия пространственной произвольной системы сил

Если система сил находится в равновесии, то ее главный вектор и главный момент равны нулю:

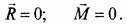
Эти векторные равенства приводят к следующим шести скалярным равенствам:

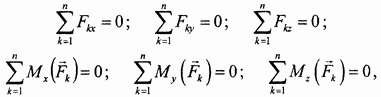
которые называются условиями равновесия пространственной произвольной системы сил.

Первые три условия выражают равенство нулю главного вектора, следующие три - равенство нулю главного момента системы сил.

В этих условиях равновесия должны учитываться все действующие силы - как активные (задаваемые), так и реакции связей. Последние заранее неизвестны, и условия равновесия становятся уравнениями для определения этих неизвестных - уравнениями равновесия.

Поскольку максимальное число уравнений равно шести, то в задаче на равновесие тела под действием произвольной пространственной систе-мы сил можно определить шесть неизвестных реакций. При большем количестве неизвестных задача становится статически неопределенной.

И еще одно замечание. Если главный вектор и главный момент относительно некоторого центра О равны нулю, то они будут равны нулю относительно любого другого центра. Это прямо следует из материала о перемене центра приведения (доказать самостоятельно). Следовательно, если условия равновесия тела выполняются в одной системе координат, то они будут выполняться и в любой другой неподвижной системе координат. Иными словами, выбор координатных осей при составлении уравнений равновесия совершенно произволен.

Пример.

Прямоугольная плита (рис. 51, а) весом удерживается в горизонтальном положении сферическим шарниром О, подшипником А и тросом BE, причем точки находятся на одной вертикали. В точке D к плите приложена сила 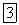, перпендикулярная стороне OD и наклоненная к плоскости плиты под углом 45°. Определить натяжение троса и реакции опор в точках Он А, если и .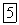

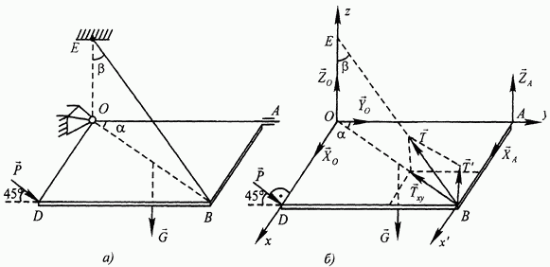
Рис. 51.

Для решения задачи рассматриваем равновесие плиты. К активным силам Р, G добавляем реакции связей - составляющие реакции сферического шарнира, реакции , подшипника, реакцию троса. Одновременно вводим координатные оси Oxyz (рис. 51, б). Видно, что полученная совокупность сил образует произвольную пространственную систему, в которой силы неизвестны.

Для определения неизвестных составляем уравнения равновесия.

Начинаем с уравнения проекций сил на ось :

Поясним определение проекции вычисление осуществляется в два приема- вначале определяетсяпроекция силы Т на плоскость , далее, проектируя на осъ х (удобнее на ось , параллельную ), находим (см. рис. 51,б):

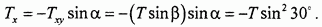
Этим способом двойного проектирования удобно пользоваться, когда линия действия силы и ось не пересекаются. Далее составляем:

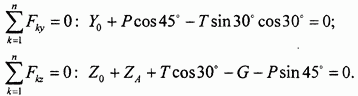
Уравнение моментов сил относительно оси имеет вид:

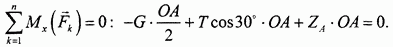
Моменты сил в уравнении отсутствуют, так как эти силы либо пересекают ось х(), либо ей параллельны . В обоих этих случаях момент силы относительно оси равен нулю (см. с. 41).

Вычисление момента силы часто облегчается, если силу разложить подходящим образом на составляющие и воспользоваться теоремой Вариньона. В данном случае это удобно сделать для силы . Разлагая ее на горизонтальную и вертикальную составляющие, можем написать:

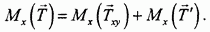
Но (сила пересекает ось х), второе же слагаемое легко вычисляется:

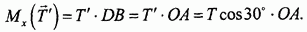
Далее составляем остальные уравнения моментов:

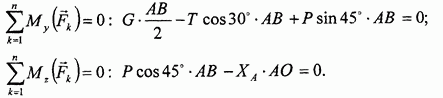
Момент силы Т в последнем уравнении отсутствует, так как линия действия силы пересекается с осью z (в точке Е).

Мы получили шесть уравнений, содержащих шесть неизвестных. Решая их, определяем все искомые реакции.

Из последних двух уравнений, содержащих лишь по одной неизвестной, сразу находим и Т:

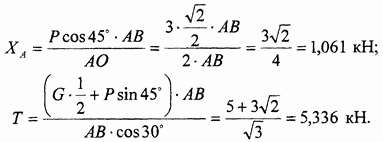
Подставляя найденные значения реакций в остальные уравнения, определяем значения других неизвестных:

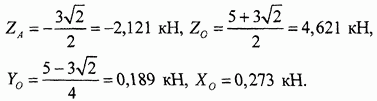
Отрицательный знак реакции означает, что ее действительное противоположно принятому в расчетах (указанному на рис. 51, б).

Date: 2015-07-27; view: 886; Нарушение авторских прав