Вычисление и построение главного вектора и главного момента

Выбираем систему координатных осей Oxyz (рис. 48) и вычисляем проекции главного вектора как алгебраические суммы проекций всех заданных сил на выбранные оси:

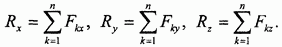
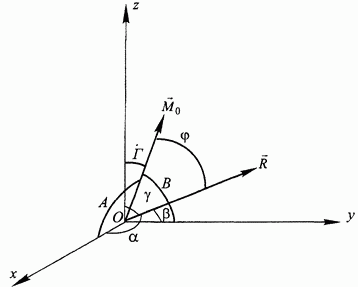
Рис. 48.

По найденным проекциям, откладывая соответствующие отрезки вдоль координатных осей (с учетом знака проекции), строим прямоугольный параллелепипед. Направленная диагональ, проведенная из начала координат в противоположную вершину параллелепипеда, определяет главный вектор R (см. также рис. 26).

Модуль и направляющие косинусы главного вектора определяются следующими вытекающими из построения формулами:

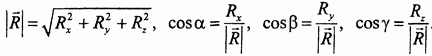
Совершенно аналогично определяются проекции, модуль и направляющие косинусы главного момента:

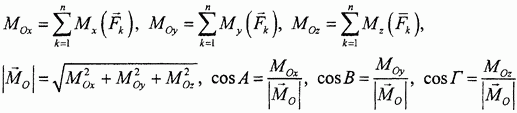
К формулам для вычисления проекций главного момента необходимо привести следующие пояснения.

Главный момент, по определению, есть векторная сумма моментов всех сил центра О. Следовательно, его проекции на координатные оси равны алгебраическим суммам проекций на эти оси векторов-моментов сил относительно центра О, то есть величин

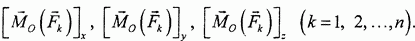
Но эти величины, по определению момента силы относительно оси, являются моментами сил относительно соответствующих координатных осей:

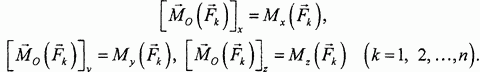
Отсюда непосредственно следуют написанные выше выражения для величин .

Косинус угла 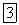между главным вектором и главным моментом определяется так:

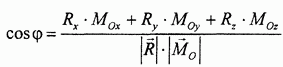
Формула получается следующим образом. По определению скалярного произведения векторов R и имеем:

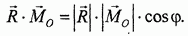
С другой стороны, эта же величина может быть вычислена через проекции векторов-сомножителей:

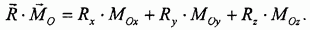
Приравнивая правые части и разрешая полученное уравнение относительно coscp, приходим к написанной формуле.

Date: 2015-07-27; view: 556; Нарушение авторских прав