Алгебраический момент силы

Наряду с общим понятием момента силы относительно точки как вектора, в статике широко используется понятие алгебраического момента силы. Алгебраическим моментом силы относительно данной точки О (обозначается ) называется произведение модуля силы на плечо, взятое со знаком плюс или минус.

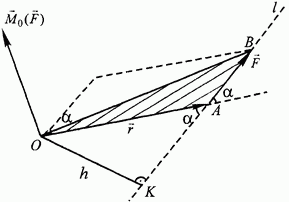
Рис. 6.

Правило знаков принимается следующее: если плоскость, образованная вектором силы и точкой О, стремится повернуться под действием силы вокруг точки О против движения часовой стрелки, то следует брать знак плюс, если по движению часовой стрелки - то знак минус.

Алгебраический момент силы используется, например, в случае системы сил, линии действия которых расположены в одной плоскости (плоской системы сил).

Пример.

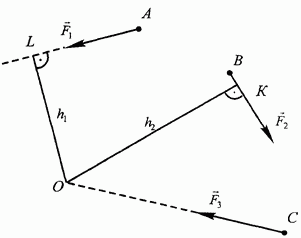
Рис. 7

Силы расположены в одной плоскости. Найти алгебраические моменты этих сил относительно точки О, взятой в той же плоскости (рис. 7).

Из моментной точки опускаем перпендикуляры на линии действия сил и получаем: 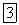плечо силы относительно точки О; 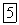плечо силы относительно той же точки. Линия действия силы проходит через точку О, поэтому . Учитывая правило знаков, для алгебраических моментов находим:

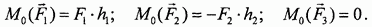
Аксиома 3 (правило параллелограмма сил)

Равнодействующая двух сил, приложенных к твердому телу в одной точке, приложена в той же точке и равна их геометрической сумме (рис. 8):

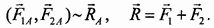
Аксиома 4 (о равенстве действия и противодействия)

Силы взаимодействия двух тел равны по величине и направлены по одной прямой в противоположные стороны (рис. 9).

Однако эти силы не образуют уравновешенную систему, поскольку приложены к разным телам.

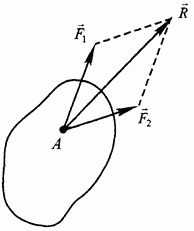
Рис. 8

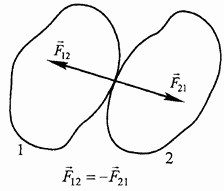
Рис. 9

Все реальные твердые тела несколько изменяют свою форму (деформируются) под действием приложенных сил. Могут изменять форму (взаимное положение) и несколько абсолютно твердых тел, сочлененных в единую систему (например, цепь, которая состоит из отдельных шарнирно-сочлененных звеньев). Следующая аксиома относится именно к таким материальным телам.

Аксиома 5 (о затвердевании)

Равновесие деформируемого твердого тела не изменится, если оно станет абсолютно твердым (неизменяемым).

Смысл этой аксиомы состоит в следующем. Пусть имеем изменяемую систему абсолютно твердых тел, находящуюся в покое под действием приложенной системы сил (рис. 10, а). Из данной аксиомы следует, что состояние покоя системы не нарушится, если ее превратить в неизменяемую систему (например, дополнив шарнирное соединение тел сварным швом, как показано на рис. 10, б). Эта аксиома широко используется в статике при исследовании равновесия систем, состоящих из нескольких абсолютно твердых тел, а также в курсе сопротивления материалов, где изучается равновесие упругого (деформируемого) тела.

Чтобы сформулировать следующую аксиому, потребуется познакомиться с новыми понятиями. Во введении уже было дано понятие свободного твердого тела - это чгело, которое можно переместить в любом направлении в окружающем пространстве. Часто, однако, приходится встречаться со случаем, когда перемещения тела в некоторых направлениях оказываются невозможными, так как этому препятствуют другие тела, с которыми рассматриваемое тело скреплено или соприкасается. Такое тело называется несвободным.

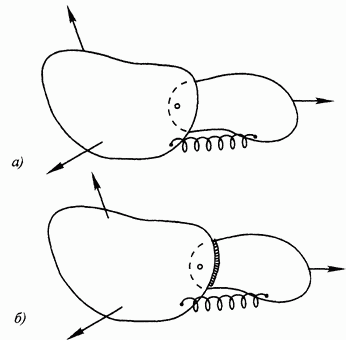
Рис. 10.

В случае несвободного тела мы имеем, с одной стороны, выделенное тело, состояние которого нас интересует, и, с другой стороны, имеем тела, которые ограничивают перемещения выделенного тела. Эти последние называются связями, а силы, с которыми связи действуют на выделенное тело, называются реакциями связей. Сформулируем теперь аксиому, называемую аксиомой освобождаемости от связей.

Аксиома 6 (освобождаемости от связей)

Состояние покоя или движения несвободного тела не изменится, если связи отбросить, а их действие на тело заменить реакциями.

Из этой аксиомы следует, что любое несвободное тело можно рассматривать как свободное. Для этого достаточно связи мысленно отбросить, а их действие на тело заменить реакциями отброшенных связей.

Полученное в результате освобождения от связей свободное тело находится под действием двоякого рода сил - сил задаваемых и реакций связей. Задаваемые силы называются также активными силами, а реакции связей - пассивными силами, поскольку они заранее неизвестны и всецело зависят от величин, направлений и точек приложения активных сил.

Пример.

Дана балка АВ, закрепленная одним концом к неподвижному основанию при помощи цилиндрического шарнира А и удерживаемая в равновесии в горизонтальном положении невесомой нитью ВС, прикрепленной к наклонной стене в точке С. На балку действуют собственный вес G и сила Р (рис. 11, а). Освободить балку от наложенных связей.

В данном случае выделенным телом является балка АВ. Ее перемещения ограничены шарниром А и нитью ВС, которые являются связями. Мысленно отбрасываем связи и прикладываем к балке соответствующие реакции. Реакция нити направлена всегда вдоль нити. В самом деле, выделив отдельно нить, видим, что она находится в равновесии под действием двух сил - силы , действующей со стороны балки, и силы , действующей со стороны стены (рис. 11, б). Нить, таким образом, находится в равновесии под действием двух сил, и из аксиомы 1 следует, что эти силы направлены вдоль прямой ВС. Сила , по смыслу, представляет собой силу, с которой балка действует на нить. Реакция же нити суть сила, с которой нить (связь) действует на балку. Отсюда, в полном соответствии с аксиомой 4 о равенстве действия и противодействия, приходим к выводу, что реакция нити направлена вдоль нити от точки В к точке С, что и показано на рис. 11, г.

Относительно реакции шарнира только то, что она: 1) проходит через центр шарнира А и 2) лежит в плоскости, перпендикулярной оси шарнира. Следовательно, это есть неизвестный вектор в плоскости , перпендикулярной оси шарнира. Его удобно представить в виде суммы двух составляющих и , приложенных в центре шарнира и направленных вдоль координатных осей (рис. 11, в).

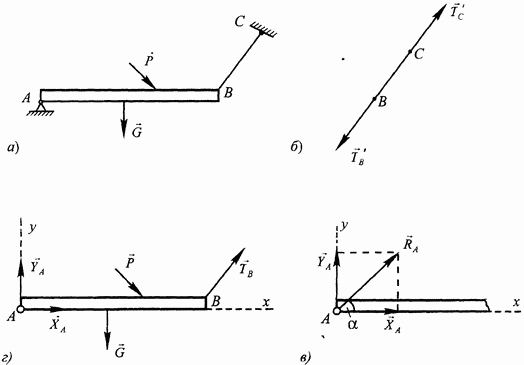
Рис. 11.

Теперь можно изобразить полную систему сил, приложенную к балке (см. рис. 11, г). Она состоит в данном случае из пяти сил, из которых две силы являются активными, а три силы - - реакциями связей.

Численные значения реакций, то есть величины наперед неизвестны и определяются в ходе решения задачи на равновесие. В этой связи заметим, что цилиндрический шарнир порождает в задачах статики две скалярные неизвестные: . Если стали известны, то величины и , определяющие модуль и направление реакции , однозначно определяются по формулам (см. рис. 11, в)

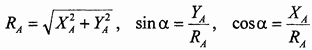
В дальнейшем условия равновесия будут формулироваться применительно к свободному твердому телу. Чтобы воспользоваться этими условиями при изучении равновесия несвободного тела, прежде всего, требуется освободить тело от наложенных связей, как это было сделано в приведенном примере. Для решения этой задачи ниже приводятся наиболее часто встречающиеся типы связей и их реакции. При этом общее правило направления реакций состоит в следующем: реакция связи всегда направлена противоположно движению, запрещаемому телу этой связью.

Date: 2015-07-27; view: 424; Нарушение авторских прав