Пара сил и ее момент

Парой сил (или просто парой) называется совокупность двух параллельных сил, равных по модулю, противоположных по направлению и приложенных в разных точках тела (рис. 30). Пару сил будем обозначать символом . Силы называются силами пары; плоскость, в которой лежат силы, называется плоскостью действия пары.

Кратчайшее расстояние между линиями действия сил пары называется плечом пары (длина h отрезка АВ на рис.

30). Так как силы можно перемещать вдоль их линий действия, в дальнейшем силы пары будем изображать приложенными к концам плеча пары.

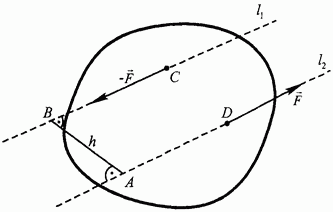
Рис. 30.

Будем также пользоваться более простым обозначением пары в виде 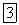, не содержащем обозначений точек приложения сил.

Пара сил характеризует особый вид взаимодействия тел, который нельзя выразить одной силой. Поэтому в статике, наряду с силами, рассматриваются отдельно также пары сил с их специфическими свойствами, правилами сложения и условиями равновесия.

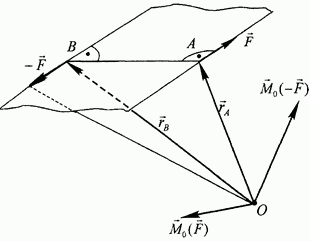
Рис. 31.

Изначально пара сил задается четырьмя векторами (рис. 31.)-двумя векторами сил пары и двумя радиусами-векторами их точек приложения. Возьмем какую-либо точку пространства в качестве центра моментов О и вычислим моменты сил пары относительно этого центра

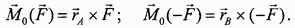
Тогда предыдущее утверждение можно выразить и в такой форме: пара сил может быть задана векторами сил пары и моментами этих сил относительно произвольного центра О. Теперь зададимся вопросом: нельзя ли пару сил задавать по-другому, желательно меньшим числом определяющих элементов?

Геометрическая сумма векторов сил пары всегда равна нулю, поэтому она не может использоваться для характеристики пары. Вычислим сумму моментов сил пары относительно точки О:

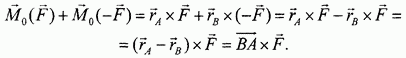
В полученном результате обращают на себя внимание два обстоятельства.

1. В то время как сумма векторов сил пары всегда равна нулю, сумма моментов сил пары отлична от нуля.

2. Сумма моментов сил пары не зависит от выбора центра моментов- векторы 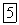зависящие от выбора точки О, выпали из окончательного выражения для искомой суммы.

Таким образом, сумма моментов сил пары оказывается зависящей только от элементов самой пары - плоскости действия пары, модуля сил и плеча пары. Это наводит на мысль использовать эту величину в качестве характеристики пары сил. В дальнейшем сумму моментов сил пары будем называть моментом этой пары. Поскольку момент пары не зависит от выбора центра моментов, то он является свободным вектором - его можно прикладывать в любой точке твердого тела, на которое действует данная пара сил.

Итак, на вопрос о том, можно ли задавать пару сил более простым способом, получен утвердительный ответ: пару сил можно характеризовать, задавая лишь один вектор - момент пары. Моментом пары сил называется свободный вектор , равный геометрической сумме моментов сил пары относительно произвольно выбранной точки О пространства

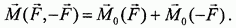
Здесь следует заметить, что приведенные рассуждения имеют скорее наводящий характер и не являются строгим доказательством только что сформулированного вывода. Однако в статике имеется ряд теорем, в которыхсделанный вывод получает строгое обоснование. С этими теоремами можно познакомиться по полным учебникам по теоретической механике.

Воспользовавшись произволом в выборе точки О в определении момента пары, можно прийти к более простому способу вычисления момента. Примем в качестве центра моментов точку приложения силы -F (точку В на рис. 31). Тогда можно написать

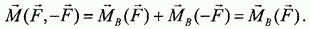
Здесь учтено, что так как сила -F проходит через точку В. Если за центр моментов принять точку А, в которой приложена сила F, то в нуль обращается момент силы F, и мы получаем

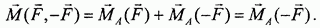
Это приводит к еще одному правилу для вычисления момента пары: момент пары сил равен моменту одной из сил пары относительно точки приложения другой силы.

Тем самым определение момента пары сводится к вычислению и построению момента силы относительно точки, подобно рассмотренному ранее (см. стр. 12).

В итоге приходим к следующему выводу: момент пары сил есть вектор, численно равный произведению модуля сил пары на плечо пары и направленный перпендикулярно плоскости действия пары в ту сторону, из которой "вращение" пары видно происходящим против движения часовой стрелки (правило буравчика); в качестве точки приложения момента пары может быть взята любая точка тела.

Алгебраическим моментом пары называется произведение модуля сил пары на плечо пары, взятое со знаком плюс, если пара "вращает" свою плоскость против движения часовой стрелки, и со знаком минус, если наоборот.

Примеры.

На рис. 32 изображена пара сил , действующая в плоскости диска радиуса R, установленного перпендикулярно к оси вращения. Плечо пары равно диаметру диска, модуль момента пары равен

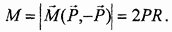
Момент пары направлен перпендикулярно плоскости диска и может быть приложен в любой точке диска.

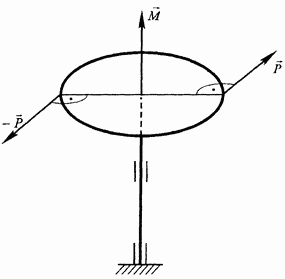
Рис. 32.

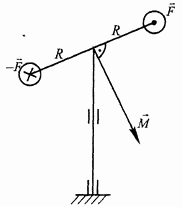
Рис. 33.

На рис. 33 показан аналогичный случай, но изображенный в плоской проекции. Здесь силы пары () направлены перпендикулярно плоскости чертежа (знаком изображаются векторы, направленные , знаком - от читателя). Момент пары по модулю равен , перпендикулярен плоскости диска и лежит в плоскости чертежа (точнее, может быть перенесен параллельно себе в плоскость чертежа).

Еще два примера построения момента пары содержатся на рис. 34. Модули моментов изображенных пар имеют значения:

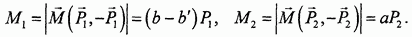
Векторы-моменты пар имеют проекции:

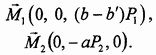
Свойства пары сил

1. Можно изменять величину сил и плечо пары, оставляя без изменения величину момента и направление "вращения" сил пары.

2. Пару сил можно как угодно перемещать в своей плоскости действия.

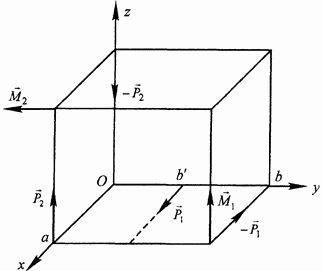
Рис. 34.

3. Пару сил можно перемещать параллельно себе в любую плоскость, неизменно связанную с телом, к которому она приложена.

Перечисленные в этих свойствах действия не изменяют ни величину, ни направление момента пары, поэтому являются эквивалентными преобразованиями пары.

В приведенных выше примерах речь шла о построении момента по заданным элементам пары - плоскости действия, силам и плечу пары. Можно ставить и обратную задачу - построить пару сил по ее моменту. Пусть требуется построить пару сил по ее моменту М (рис. 35, а). Для этого строим плоскость П, перпендикулярную линии действия момента (рис. 35, б). Эта плоскость будет служить плоскостью действия пары. В этой плоскости располагаем две силы по следующему правилу. Направление сил выбирается так, чтобы из конца вектора-момента М силы были видны ориентированными против движения часовой стрелки. Величина сил и плечо пары могут быть любыми (свойство 1), но чтобы их произведение было равно модулю момента пары: .

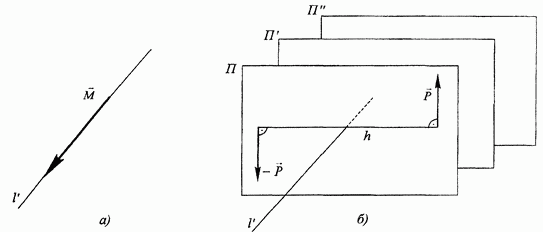
Рис. 35.

Согласно свойству 3 плоскостью действия пары будет являться и любая другая плоскость , параллельная плоскости П.

В дальнейшем, имея дело с парами сил, мы будем указывать только их векторы-моменты и т.д., прибегая к построению самой пары лишь при необходимости.

Date: 2015-07-27; view: 422; Нарушение авторских прав