Переход к новому осуществляется в результате пересчета симплексной таблицы методом Жордана - Гаусса

Разделим все элементы ведущей строки предыдущей симплексной таблицы на ведущий элемент и результаты деления занесем в строку следующей симплексной таблицы. В результате этого на месте разрешающего элемента в следующей симплексной таблице запишем 1, а в остальных клетках j столбца, включая клетку столбца целевой функции, записываем нули.

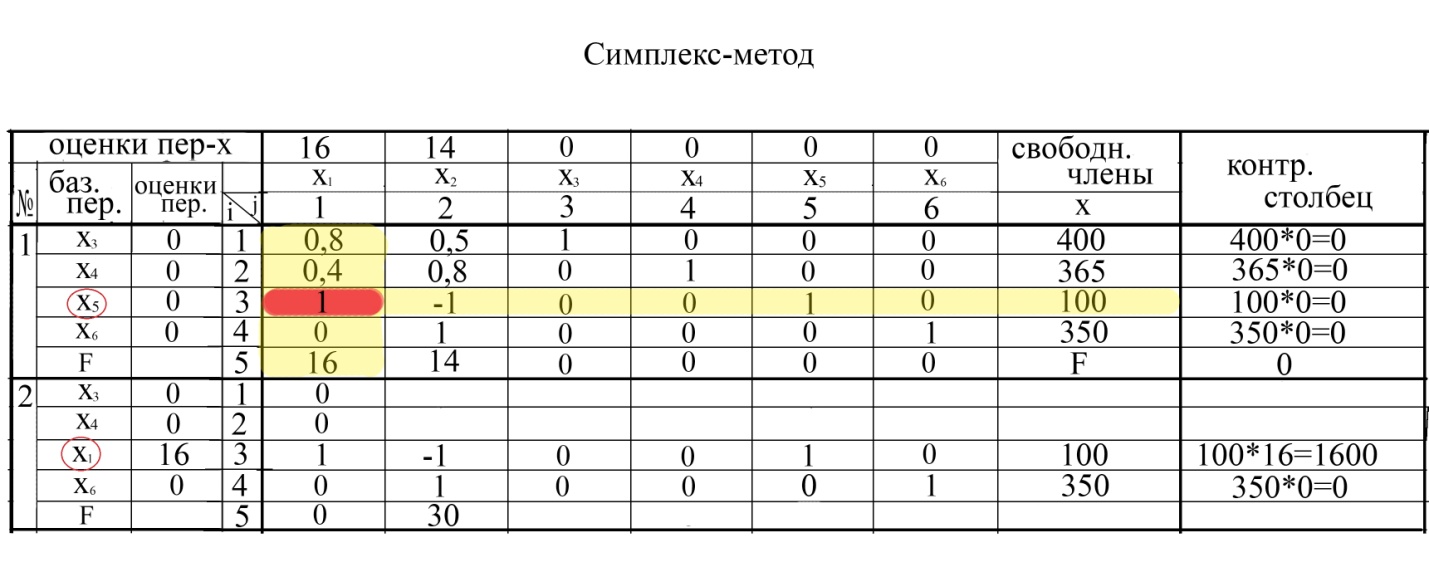
Если в ведущем столбце есть нулевой коэффициент, то соответствующая ему строка переносится в следующую итерацию без изменений (строка 4 первой итерации) (см.табл.).

Кроме этого на втором шаге свободная переменная, соответствующая ведущему столбцу (x₁), заменяет базисную переменную, соответствующую ведущей строке (x₅) (см.табл.) вместе со своей оценкой.

Остальные коэффициенты пересчитываются по правилу прямоугольника следующим образом. Для каждого преобразуемого коэффициента строится прямоугольник, две противоположных вершины которого образуют преобразуемый и ведущий коэффициент. Вычисления производятся так: новое значение преобразуемого коэффициента равно его старому значению минус произведение коэффициентов, стоящих на противоположной диагонали и деленные на ведущий коэффициент.

Например, нам необходимо найти новое значение коэффициента a¹₅₂ =14 на втором шаге (см.табл.).

Прямоугольник для него будет:

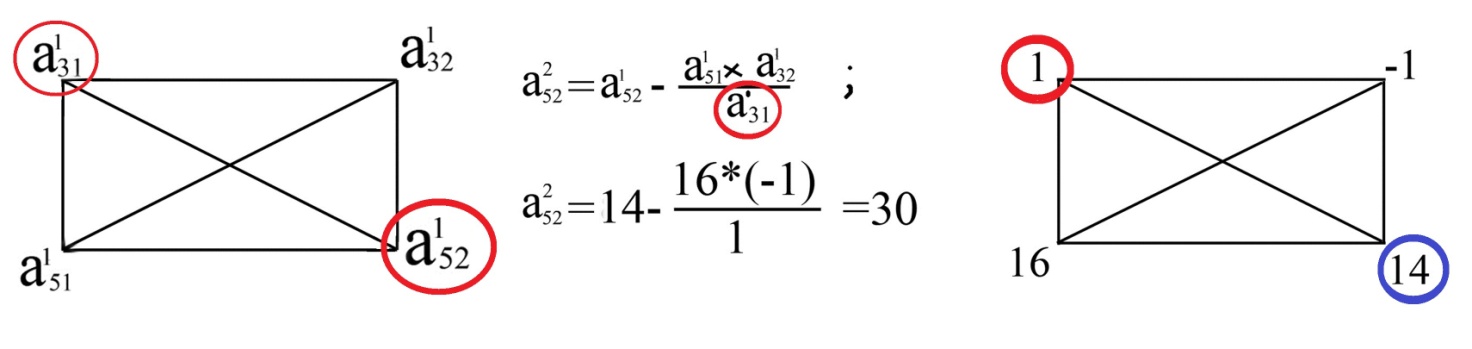
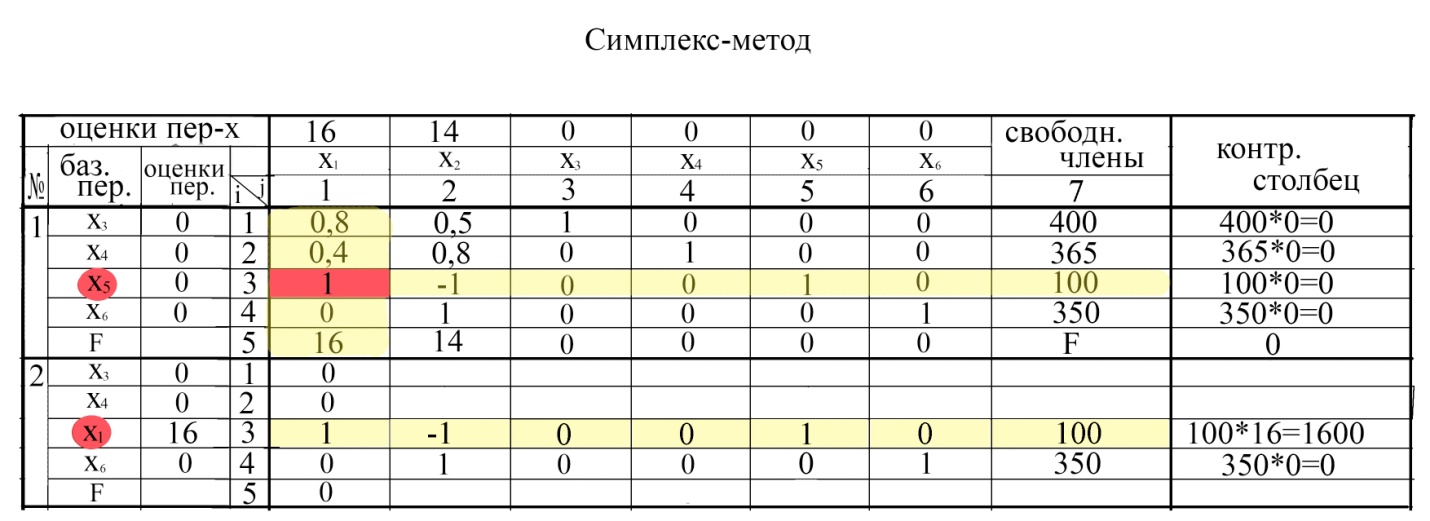
Также находим значения всех коэффициентов на втором шаге (см.табл.).

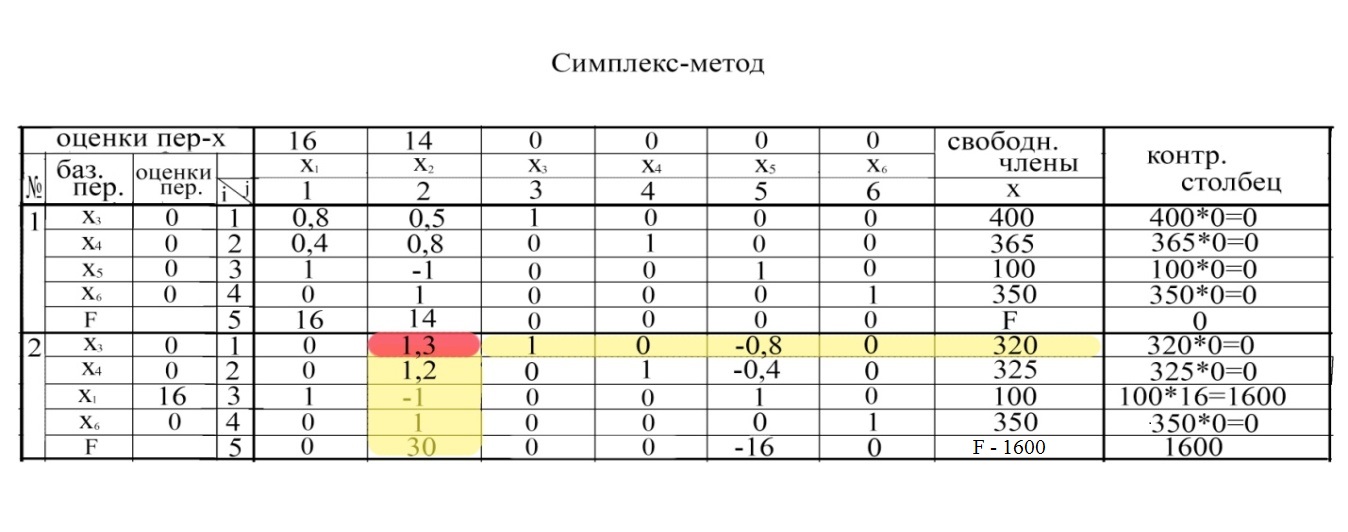
Таким образом, на втором шаге (второй итерации) мы получили следующий план (см.табл.):

- выпускается 100 кг сливочного мороженого (x₁=100); шоколадное не выпускается (x₂=0);

- избыток наполнителя составляет 325 кг (x₄=325);

- спрос на сливочное мороженое удовлетворяется полностью (уравнение 3 системы 3.6 (x₁-x₂=100; 100-0=100, т.е. x₅=0);

- избыток спроса на шоколадное мороженое составляет 350 кг (x₆=350);

- доход составляет 1600 руб.

Далее возвращаемся к этапу 3 и проверяем полученный план на оптимальность. Из строки целевой функции видно, что она содержит положительный коэффициент c ₅₂ = 30 (см.табл.), т.е. план не оптимальный и его можно улучшить путем введения в план выпуск шоколадного мороженого (x₂), так как любое значение x₂>0 увеличивает значение целевой функции.

Выполняя последовательно этапа 3-5, получаем окончательную симплексную таблицу

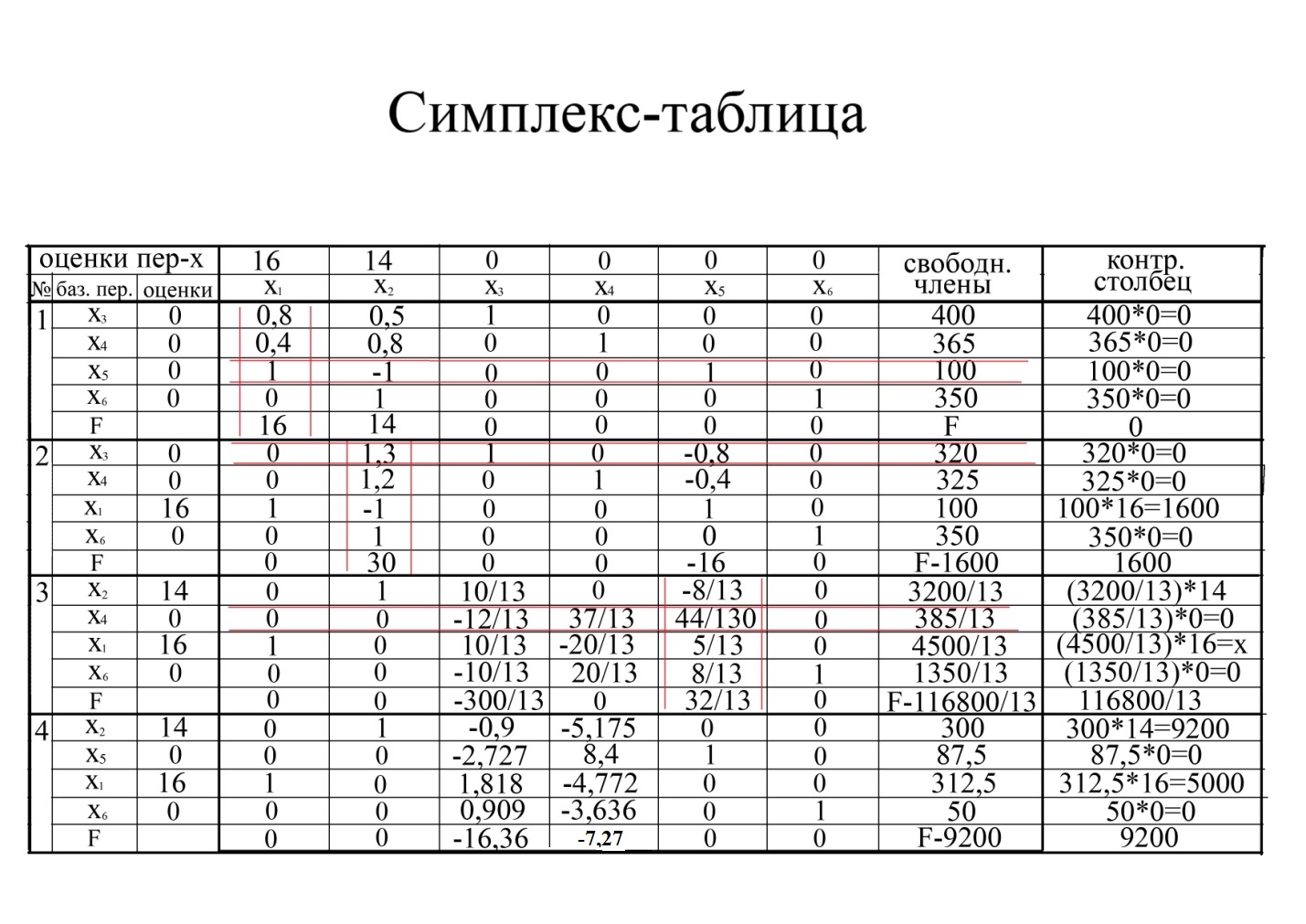
В этой таблице все коэффициенты в строке целевой функции отрицательные или равные нулю, т.е. полученный план оптимален, т.е. нет ни одной переменной, введение которой в план увеличилось бы значение целевой функции в 9200 руб.

Оптимальное решение:

x₁=312,5; x₂=300; x₃=x₄ =0; x₅= 87,5 x₆ =312,5; F(x)=9200.

Date: 2015-07-27; view: 964; Нарушение авторских прав