
Полезное:
Как сделать разговор полезным и приятным
Как сделать объемную звезду своими руками
Как сделать то, что делать не хочется?
Как сделать погремушку
Как сделать так чтобы женщины сами знакомились с вами
Как сделать идею коммерческой
Как сделать хорошую растяжку ног?
Как сделать наш разум здоровым?
Как сделать, чтобы люди обманывали меньше
Вопрос 4. Как сделать так, чтобы вас уважали и ценили?
Как сделать лучше себе и другим людям
Как сделать свидание интересным?

Категории:
АрхитектураАстрономияБиологияГеографияГеологияИнформатикаИскусствоИсторияКулинарияКультураМаркетингМатематикаМедицинаМенеджментОхрана трудаПравоПроизводствоПсихологияРелигияСоциологияСпортТехникаФизикаФилософияХимияЭкологияЭкономикаЭлектроника

II. Вычисление оценок математического ожидания и дисперсии
|
|
Оценки математического ожидания и дисперсии вычисляются по формулам
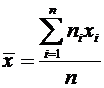 ,
, 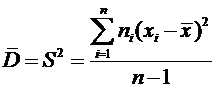 , (1)
, (1)
где 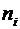 — частота варианты
— частота варианты 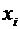 в выборке объема
в выборке объема 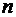 .
.
Если объем выработки велик, то вычисление точечных оценок математического ожидания 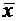 и дисперсии
и дисперсии 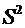 по формулам (1) громоздко. Для сокращения вычислений элементам выборки, попавшим в
по формулам (1) громоздко. Для сокращения вычислений элементам выборки, попавшим в 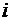 –тый интервал, припишем значения равные серединам интервалов
–тый интервал, припишем значения равные серединам интервалов
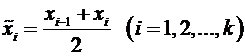 .
.
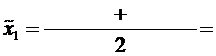 4,31
4,31 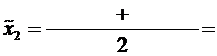 4,40
4,40
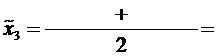 4,46
4,46 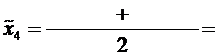 4,52
4,52

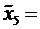 4,58 x6 =4,64
4,58 x6 =4,64
 x7 =4,70
x7 =4,70
Вносим значения в пятый столбец таблицы 1.
Для упрощения дальнейших выкладок варианты 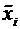 заменяем на условные варианты
заменяем на условные варианты 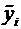 по формуле
по формуле
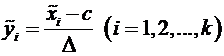 ,
,
где 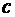 называется ложным нулем (новым началом отсчета). Ложный ноль находим по следующему правилу:
называется ложным нулем (новым началом отсчета). Ложный ноль находим по следующему правилу:
Если число интервалов нечетное, то в качестве ложного нуля берем середину среднего интервала, если четное, то середину того интервала, у которого больше частота 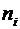 .
.
При этом варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю.
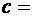 4,52
4,52
 -3,00
-3,00  -2,00
-2,00
 -1,00
-1,00  0,00
0,00

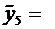 1,00 y6 = 2,00
1,00 y6 = 2,00
 y7 = 3,00
y7 = 3,00
Значения 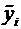 вносим в таблицу 1.
вносим в таблицу 1.
Подсчитаем произведения 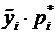 , результаты внесем в таблицу 1.
, результаты внесем в таблицу 1.
Суммируя седьмой столбец таблицы 1, вычислим значение
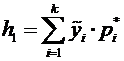 = 0,086
= 0,086
Оценим математическое ожидание по формуле
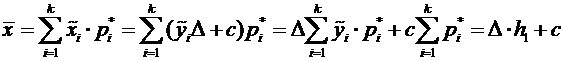 .
.
 4,53
4,53
Подсчитаем произведения 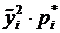 , результаты внесем в таблицу 1.
, результаты внесем в таблицу 1.
Суммируя восьмой столбец таблицы 1, вычислим значение
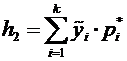 = 2,09
= 2,09
Оценим дисперсию по формуле
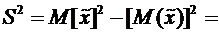
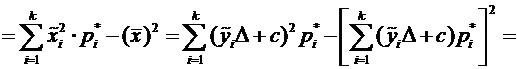
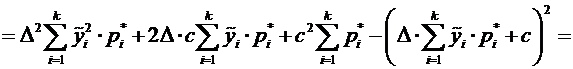
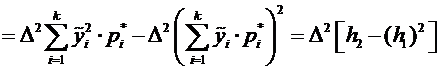
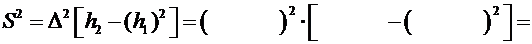
 0,00748
0,00748
.
Оценка 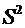 занижает дисперсию генеральной совокупности, поэтому введя поправочный коэффициент
занижает дисперсию генеральной совокупности, поэтому введя поправочный коэффициент
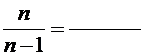
получим несмещенную оценку дисперсии
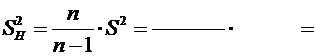 0,00759.
0,00759.
Вычислим оценку среднего квадратического отклонения
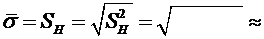 0,0871.
0,0871.
Для сравнения подсчитаем 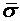 по «правилу
по «правилу 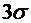 ». Так как для случайной величины, имеющей нормальное распределение, почти все рассеивания укладывается на участке
». Так как для случайной величины, имеющей нормальное распределение, почти все рассеивания укладывается на участке 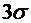 , то с помощью «правила
, то с помощью «правила 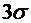 » можно ориентировочно определить оценку среднего квадратического отклонения случайной величины. Берем максимальное практически возможное отклонение от среднего значения и делим его на три.
» можно ориентировочно определить оценку среднего квадратического отклонения случайной величины. Берем максимальное практически возможное отклонение от среднего значения и делим его на три.
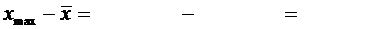 0,20
0,20
 0,22
0,22
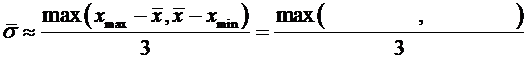
 0,0717
0,0717
Табл. 1
| Статистическое распределение выборки | 
| 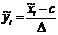
| 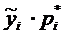
| 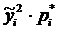
| 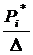
| |||
| № Кл. | Границы классов | 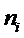
| 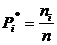
| |||||
| 4,31 (4,31;4,37) (4,37;4,43) (4,43;4,49) (4,49;4,55) (4,55;4,61) (4,61;4,66) (4,66;4,73) | 0,043 0,100 0,186 0,271 0,257 0,086 0,057 | 4,34 4,40 4,46 4,52 4,58 4,64 4,70 | -3,00 -2,00 -1,00 0,00 1,00 2,00 3,00 | -0,129 -0,200 -0,186 0,000 0,257 0,171 0,171 | 0,386 0,400 0,186 0,000 0,257 0,343 0,514 | 0,714 1,667 3,095 4,524 4,286 1,429 0,952 | ||
| ∑ | h1= =0,086 | h2= =2,09 |
Date: 2015-07-27; view: 1479; Нарушение авторских прав