IV. Проверка гипотезы о нормальном распределении случайной величины

Ввиду ограниченного числа наблюдений статистический закон распределения обычно в какой-то мере отличается от теоретического. Возникает необходимость определить: является ли расхождение между статистическим и теоретическим законами распределения следствием ограниченного числа наблюдений или оно является существенным и связано с тем, что действительное распределение случайной величины не соответствует выдвинутой гипотезе.

Для проверки гипотезы о нормальном распределении рассматриваемой величины заполним таблицу 2. Для этого:

1. Производим новую классификацию выборки: добавляем новые интервалы 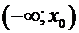и 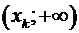к уже имеющимся и объединяем интервалы, для которых 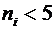в один.

После объединения количество интервалов 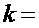5.

2. Вычисляем теоретические вероятности 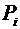попадания варианты в каждом интервале по формуле

,

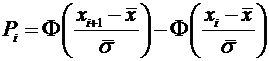где 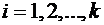, функция Лапласа

.

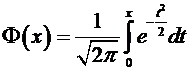0,343

0,269

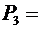0,223 P ₄=0,117 P ₅=0,048

3. Вычисляем частоты интервалов 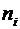и относительные частоты 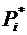с учетом объединения интервалов.

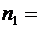10, 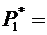0,14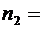3, 13, 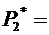0,186,

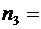19, P^*₃ = 0,271, n₄ = 18, P^*₄ = 0,117

n₅ = 10, P^*₅ = 0,048

4. Для проверки гипотезы о нормальном распределении случайной величины в качестве меры расхождения между теоретическим и статистическим распределениями выберем случайную величину 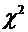(хи-квадрат)

.

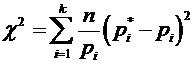
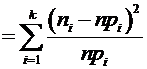Заполнив таблицу 2, вычислим значение критерия 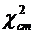(хи-квадрат статистическое).

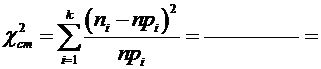35,556

Случайная величина 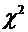распределена по закону 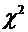с параметром 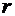, называемым числом степенной свободы.

Число параметров нормального распределения 2

Число степенной свободы 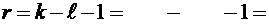2.

Расхождение между статистическим и теоретическим распределениями является не существенным, если величина 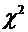не превышает критического значения .

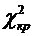При уровне значимости 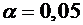и числу степенной свободы 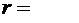находим критическое значение

5,99.

Так как

,

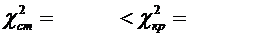то выдвинутую гипотезу о том, что случайная величина 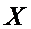распределена по нормальному закону, можно с надежностью

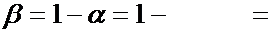
считать правдоподобной, не противоречащей опытным данным.

Табл. 2

№	Границы классов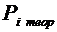
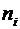
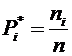
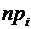
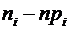
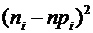
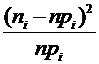
	(-∞;4,49]	0,343		0,143	24,034	-14,034	196,946	8,195
	(4,49;4,55]	0,269		0,186	18,827	-5,827	33,954	1,803
	(4,55;4,61]	0,223		0,271	15,587	3,413	11,648	0,747
	(4,61;4,67]	0,117		0,257	8,179	9,821	96,453	11,793
	(4,67;+∞)	0,048		0,143	3,373	6,627	43,913	13,018
	Σ		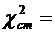					35,5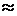56   35,556

Построим график теоретической плотности распределения

.

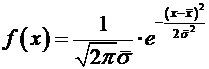Для этого возьмем 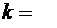7 точек с абсциссами 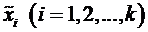из таблицы 1 и вычислим ординаты этих точек. Результат запишем в таблицу 3.

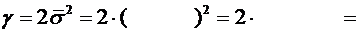0,015

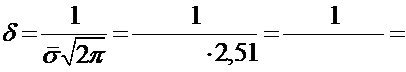4,51

Табл. 3

N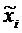
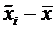
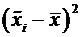
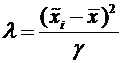
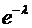
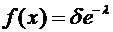
	4,34	-0,19	0,03428	2,258	0,104	0,471
	4,40	-0,13	0,01566	1,032	0,356	1,607
	4,46	-0,07	0,00424	0,280	0,756	3,410
	4,52	-0,01	0,00003	0,002	0,998	4,502
	4,58	0,05	0,00301	0,198	0,820	3,699
	4,64	0,11	0,01319	0,869	0,419	1,891
	4,70	0,17	0,03058	2,014	0,133	0,601

Для более точного построения графика вычислим точку максимума

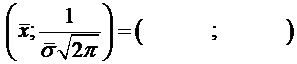,(4,53;4,58)

и точки перегиба

,

(4,61;2,78)

.

(4,48;2,78)

Сравним теоретическую и эмпирическую плотности распределения случайной величины:

Табл. 4.

N
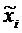
	4,34	4,40	4,46	4,52	4,58	4,64	4,70
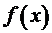
	0,471	1,607	3,410	4,502	3,699	1,891	0,601
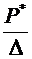
	0,714	1,667	3,095	4,524	4,286	1,429	0,952

Сравнивая значения ординат плотности распределения случайной величины и плотности относительных частот, мы наблюдаем незначительное отклонение этих величин друг от друга, что также свидетельствует о правильности выбора закона распределения.

Date: 2015-07-27; view: 1218; Нарушение авторских прав